=1, 1 =0.
2. Х+0=Х, Х⋅1=Х
3. Х+1=1, Х⋅0=0
Законы идемпотентности:
4. Х+Х=Х , Х⋅Х=Х
Законы исключения третьего и вторая форма закона непротиворечия:
_ _
5. Х+Х=1, Х⋅Х =0.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоремы алгебры логики презентация
Содержание
- 1. Теоремы алгебры логики
- 2. Закон двойного отрицания: = 6.Х=Х.
- 3. Законы де Моргана: ____
- 4. Упрощение функций и построение таблиц истинности.
- 5. Задача 1 F(X1,X2,X3)=X3⋅(X2⋅X1+X3) Решение: X3⋅(X2⋅X1+X3)={10}=
- 6. Строим таблицу истинности для полученного выражения
- 7. Задача 2 F(X1,X2,X3)=X1⋅X2⋅X3+X1+ X2+X3) Решение: {12}
- 8. Строим таблицу истинности для полученного выражения
- 9. Самостоятельно: F(X1,X2,X3)=X1+X3+X1⋅X2 2) F(X1,X2,X3)=X1+X2⋅(X1+X3⋅X2) Дома: F(X1,X2,X3)=X1+X2+X3⋅(X1+X3) Выучить наизусть теоремы алгебры логики
Закон двойного отрицания: = 6.Х=Х. Законы коммутативности: 7. Х+Y=Y+X, X⋅Y=Y⋅X. Законы поглощения: 8. X+X⋅Y=X, X⋅(X+Y)=X _
Слайд 2Закон двойного отрицания:
=
6.Х=Х.
Законы коммутативности:
7. Х+Y=Y+X, X⋅Y=Y⋅X.
Законы поглощения:
8. X+X⋅Y=X, X⋅(X+Y)=X
_ _
9. X+X⋅Y=X+Y , X⋅(X+Y)=X⋅Y.
9. X+X⋅Y=X+Y , X⋅(X+Y)=X⋅Y.
Слайд 3Законы де Моргана:
____ _ _ __
_ _
10. (X+Y)=X⋅Y, X⋅Y=X+Y.
Законы ассоциативности:
11. (X+Y)+Z=X+(Y+Z)=X+Y+Z,
(X⋅Y)⋅Z= X⋅(Y⋅Z)= X⋅Y⋅Z
Законы дистрибутивности:
12. X+Y⋅Z=(X+Y)⋅(X+Z), X⋅(Y+Z)= X⋅Y+ X⋅Z.
10. (X+Y)=X⋅Y, X⋅Y=X+Y.
Законы ассоциативности:
11. (X+Y)+Z=X+(Y+Z)=X+Y+Z,
(X⋅Y)⋅Z= X⋅(Y⋅Z)= X⋅Y⋅Z
Законы дистрибутивности:
12. X+Y⋅Z=(X+Y)⋅(X+Z), X⋅(Y+Z)= X⋅Y+ X⋅Z.
Слайд 4Упрощение функций и построение таблиц истинности.
В задачах данного раздела требуется упростить
логическую функцию F(X1,X2,X3) и построить таблицу истинности. В решениях в фигурных скобках указаны номера теорем, которые применяются для упрощения выражений.
Слайд 5Задача 1
F(X1,X2,X3)=X3⋅(X2⋅X1+X3)
Решение:
X3⋅(X2⋅X1+X3)={10}=
= X3⋅(X2⋅X1⋅X3)={11,6}=
=X3⋅X2⋅X1⋅X3={4,7} = X1⋅X2⋅X3.
Свойства констант:
_
_
1. 0=1, 1=0.
2. Х+0=Х, Х⋅1=Х
3. Х+1=1, Х⋅0=0.
Законы идемпотентности:
4. Х+Х=Х , Х⋅Х=Х
Законы исключения третьего и вторая форма закона непротворечия:
_ _
5. Х+Х=1, Х⋅Х=0.
Закон двойного отрицания:
=
6.Х=Х.
Законы коммутативности:
7. Х+Y=Y+X, X⋅Y=Y⋅X.
Законы поглощения:
8. X+X⋅Y=X, X⋅(X+Y)=X
_ _
9. X+X⋅Y=X+Y , X⋅(X+Y)=X⋅Y.
Законы де Моргана:
____ _ _ __ _ _
10. (X+Y)= X⋅Y, X⋅Y=X+Y.
Законы ассоциативности:
11. (X+Y)+Z=X+(Y+Z)=X+Y+Z, (X⋅Y)⋅Z= X⋅(Y⋅Z)= X⋅Y⋅Z
Законы дистрибутивности:
12. X+Y⋅Z=(X+Y)⋅(X+Z), X⋅(Y+Z)= X⋅Y+ X⋅Z.
1. 0=1, 1=0.
2. Х+0=Х, Х⋅1=Х
3. Х+1=1, Х⋅0=0.
Законы идемпотентности:
4. Х+Х=Х , Х⋅Х=Х
Законы исключения третьего и вторая форма закона непротворечия:
_ _
5. Х+Х=1, Х⋅Х=0.
Закон двойного отрицания:
=
6.Х=Х.
Законы коммутативности:
7. Х+Y=Y+X, X⋅Y=Y⋅X.
Законы поглощения:
8. X+X⋅Y=X, X⋅(X+Y)=X
_ _
9. X+X⋅Y=X+Y , X⋅(X+Y)=X⋅Y.
Законы де Моргана:
____ _ _ __ _ _
10. (X+Y)= X⋅Y, X⋅Y=X+Y.
Законы ассоциативности:
11. (X+Y)+Z=X+(Y+Z)=X+Y+Z, (X⋅Y)⋅Z= X⋅(Y⋅Z)= X⋅Y⋅Z
Законы дистрибутивности:
12. X+Y⋅Z=(X+Y)⋅(X+Z), X⋅(Y+Z)= X⋅Y+ X⋅Z.
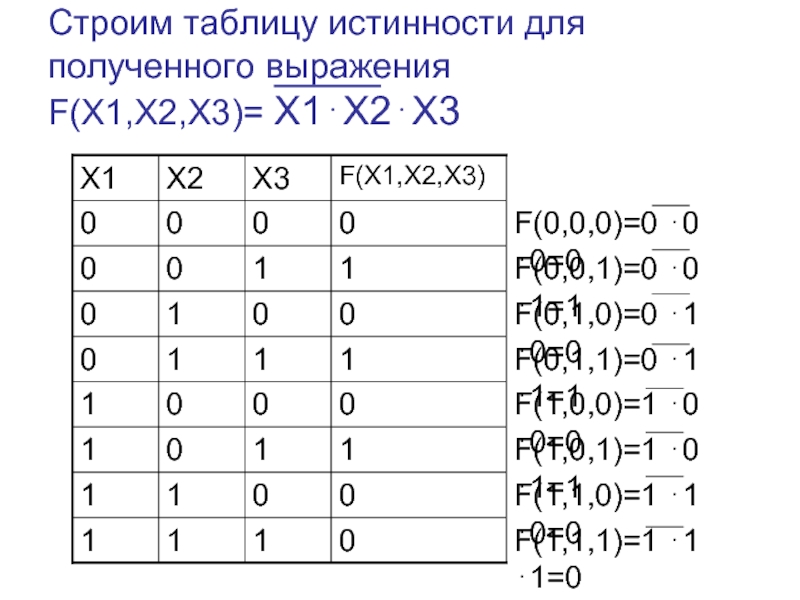
Слайд 6Строим таблицу истинности для полученного выражения
F(X1,X2,X3)= X1⋅X2⋅X3
F(1,1,1)=1 ⋅1 ⋅1=0
F(1,1,0)=1 ⋅1
⋅0=0
F(1,0,1)=1 ⋅0 ⋅1=1
F(1,0,0)=1 ⋅0 ⋅0=0
F(0,1,1)=0 ⋅1 ⋅1=1
F(0,1,0)=0 ⋅1 ⋅0=0
F(0,0,1)=0 ⋅0 ⋅1=1
F(0,0,0)=0 ⋅0 ⋅0=0
0
1
1
1
0
0
1
1
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
0
0
0
0
0
0
F(X1,X2,X3)
Х3
Х2
Х1
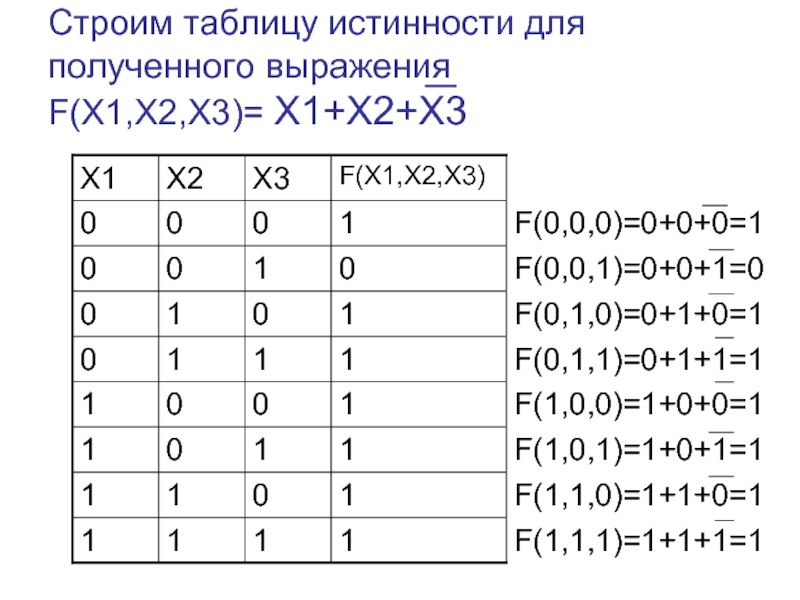
Слайд 7Задача 2
F(X1,X2,X3)=X1⋅X2⋅X3+X1+
X2+X3)
Решение: {12} =
X1⋅(X2⋅X3+1)+X2+X3={3,2}=
= X1+X2+X3
Свойства констант:
_
_
1. 0=1, 1=0.
2. Х+0=Х, Х⋅1=Х
3. Х+1=1, Х⋅0=0.
Законы идемпотентности:
4. Х+Х=Х , Х⋅Х=Х
Законы исключения третьего и вторая форма закона непротворечия:
_ _
5. Х+Х=1, Х⋅Х=0.
Закон двойного отрицания:
=
6.Х=Х.
Законы коммутативности:
7. Х+Y=Y+X, X⋅Y=Y⋅X.
Законы поглощения:
8. X+X⋅Y=X, X⋅(X+Y)=X
_ _
9. X+X⋅Y=X+Y , X⋅(X+Y)=X⋅Y.
Законы де Моргана:
____ _ _ __ _ _
10. (X+Y)= X⋅Y, X⋅Y=X+Y.
Законы ассоциативности:
11. (X+Y)+Z=X+(Y+Z)=X+Y+Z, (X⋅Y)⋅Z= X⋅(Y⋅Z)= X⋅Y⋅Z
Законы дистрибутивности:
12. X+Y⋅Z=(X+Y)⋅(X+Z), X⋅(Y+Z)= X⋅Y+ X⋅Z.
1. 0=1, 1=0.
2. Х+0=Х, Х⋅1=Х
3. Х+1=1, Х⋅0=0.
Законы идемпотентности:
4. Х+Х=Х , Х⋅Х=Х
Законы исключения третьего и вторая форма закона непротворечия:
_ _
5. Х+Х=1, Х⋅Х=0.
Закон двойного отрицания:
=
6.Х=Х.
Законы коммутативности:
7. Х+Y=Y+X, X⋅Y=Y⋅X.
Законы поглощения:
8. X+X⋅Y=X, X⋅(X+Y)=X
_ _
9. X+X⋅Y=X+Y , X⋅(X+Y)=X⋅Y.
Законы де Моргана:
____ _ _ __ _ _
10. (X+Y)= X⋅Y, X⋅Y=X+Y.
Законы ассоциативности:
11. (X+Y)+Z=X+(Y+Z)=X+Y+Z, (X⋅Y)⋅Z= X⋅(Y⋅Z)= X⋅Y⋅Z
Законы дистрибутивности:
12. X+Y⋅Z=(X+Y)⋅(X+Z), X⋅(Y+Z)= X⋅Y+ X⋅Z.
Слайд 8Строим таблицу истинности для полученного выражения
F(X1,X2,X3)= X1+X2+X3
F(1,1,1)=1+1+1=1
F(1,1,0)=1+1+0=1
F(1,0,1)=1+0+1=1
F(1,0,0)=1+0+0=1
F(0,1,1)=0+1+1=1
F(0,1,0)=0+1+0=1
F(0,0,1)=0+0+1=0
F(0,0,0)=0+0+0=1
1
1
1
1
1
0
1
1
1
1
0
1
1
0
0
1
1
1
1
0
1
0
1
0
0
1
0
0
1
0
0
0
F(X1,X2,X3)
Х3
Х2
Х1
Слайд 9Самостоятельно:
F(X1,X2,X3)=X1+X3+X1⋅X2
2) F(X1,X2,X3)=X1+X2⋅(X1+X3⋅X2)
Дома:
F(X1,X2,X3)=X1+X2+X3⋅(X1+X3)
Выучить наизусть теоремы алгебры логики
