- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема урока: Решение задач презентация
Содержание
- 1. Тема урока: Решение задач
- 2. Цели урока Повторить понятия медианы,
- 3. Решение задач по медианам, биссектрисам, высотам треугольника. Равнобедренный треугольник. 21.11.07
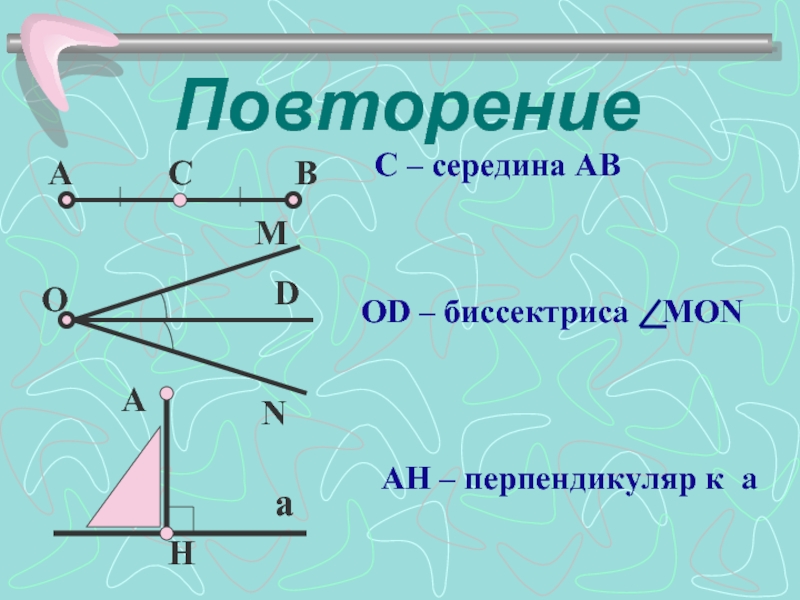
- 4. Повторение С – середина АВ AH – перпендикуляр к а
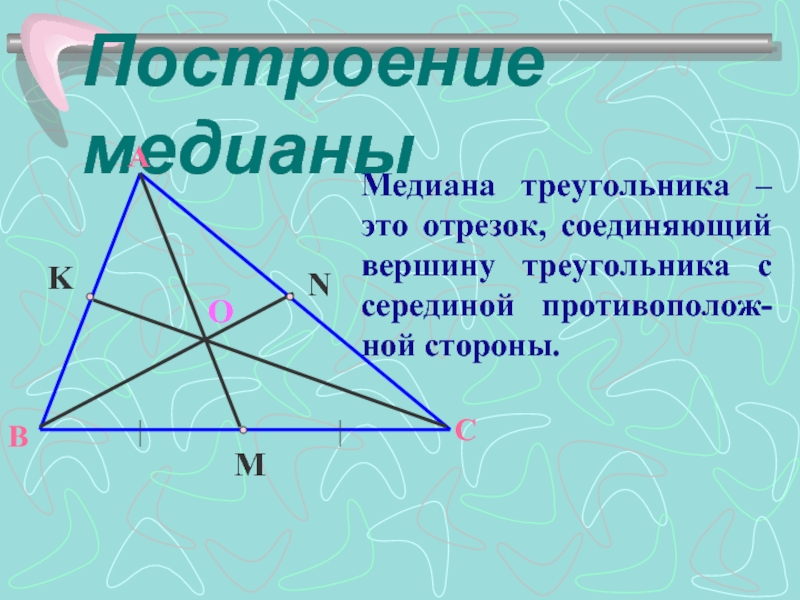
- 5. Построение медианы O Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противополож-ной стороны.
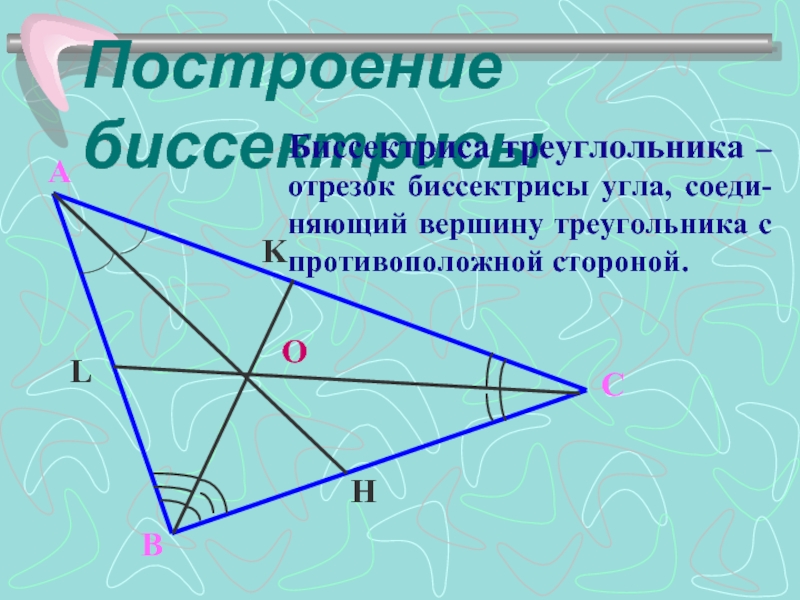
- 6. Построение биссектрисы H K L O Биссектриса
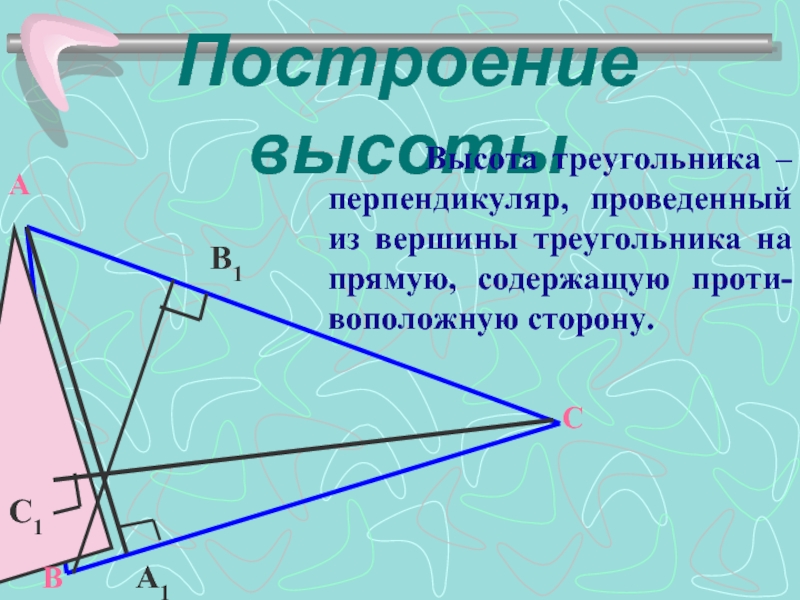
- 7. Построение высоты
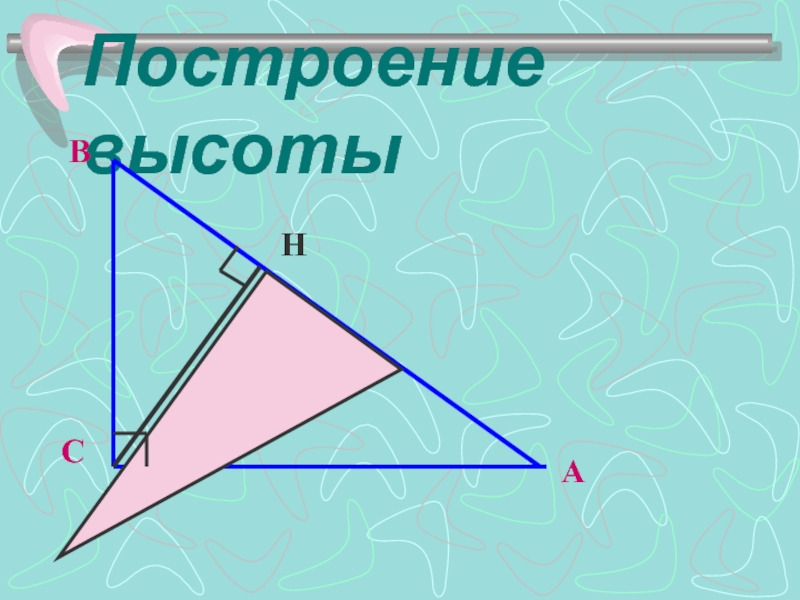
- 8. Построение высоты H
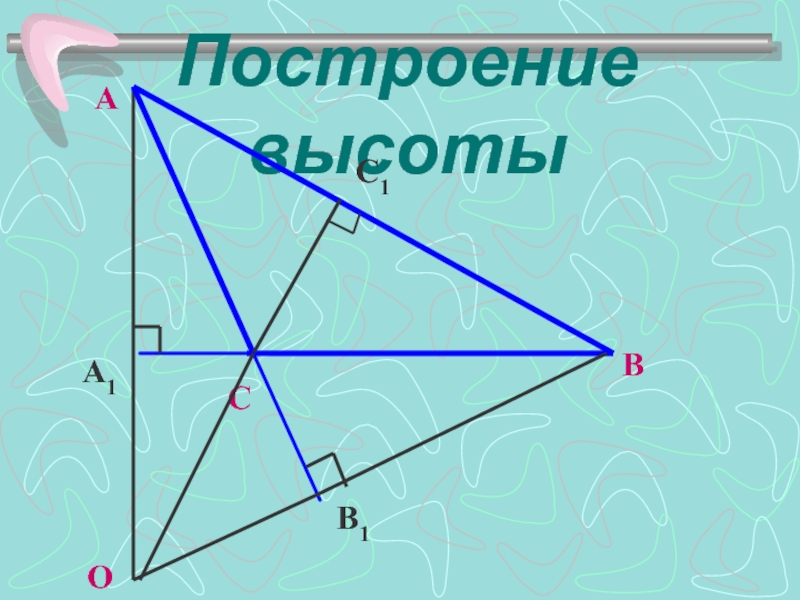
- 9. Построение высоты C1 B1 A1 O
- 10. Основные свойства медиан, биссектрис и высот.
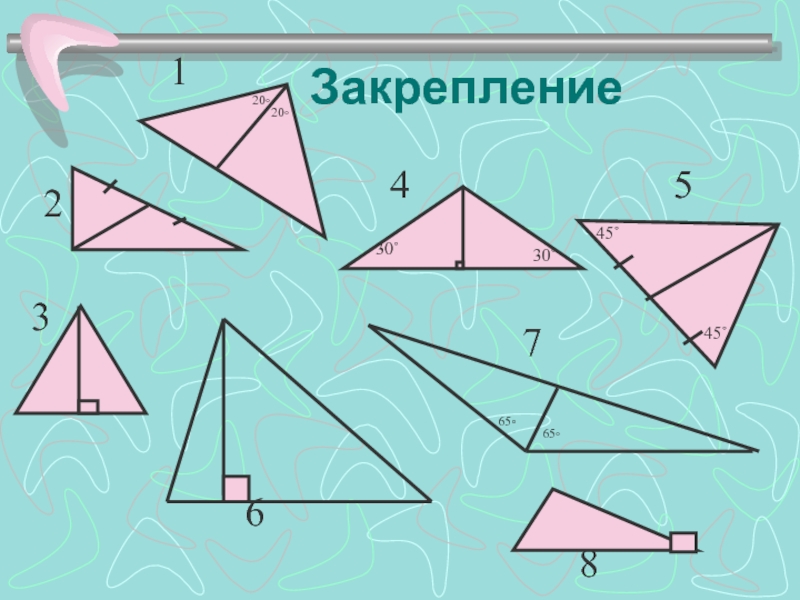
- 11. Закрепление
- 12. Медиана: 2, 5. Высота: 3, 6,
- 13. А В С К Дано:
- 14. Закрепление Дано: ОH и ON – высоты
- 15. № 113. в М Р О N
- 16. Самостоятельная работа Вариант 1. А В
- 17. Домашнее задание № 113 (б), № 117 Спосибо за урок!
Слайд 1Тема урока: «Решение задач»
Комбинированный урок по геометрии
в 7 классе
Авторы:
Карпунина
средней школы №5 г. Саранска
Слайд 2Цели урока
Повторить понятия медианы, биссектрисы, высоты треугольника;
Повторить свойства равнобедренного
показать применение данных понятий при решении геометрических задач.
Слайд 3Решение задач по медианам, биссектрисам, высотам треугольника.
Равнобедренный треугольник.
21.11.07
Слайд 5Построение медианы
O
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой
Слайд 6Построение биссектрисы
H
K
L
O
Биссектриса треуглольника – отрезок биссектрисы угла, соеди-няющий вершину треугольника с
Слайд 7Построение высоты
Высота треугольника – перпендикуляр, проведенный из
A1
C1
B1
Слайд 10
Основные свойства медиан,
биссектрис и высот.
Медианы треугольника пересекаются
в одной точке, внутри
2. Биссектрисы треугольника пересекаю-
тся в одной точке, внутри треугольника.
3. Высоты треугольника пересекаются
в одной точке внутри треугольника
или на сторонах прямого угла, или
на продолжении сторон тупого угла.
Слайд 13
А
В
С
К
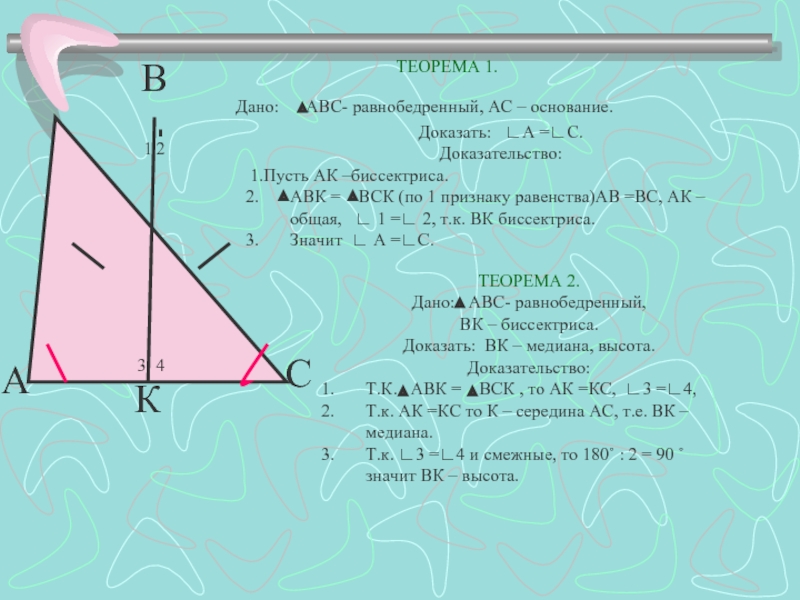
Дано: АВС- равнобедренный, АС – основание.
Доказать: ∟А
Доказательство:
1.Пусть АК –биссектриса.
АВК = ВСК (по 1 признаку равенства)АВ =ВС, АК – общая, ∟ 1 =∟ 2, т.к. ВК биссектриса.
Значит ∟ А =∟С.
1
2
ТЕОРЕМА 2.
Дано: АВС- равнобедренный,
ВК – биссектриса.
Доказать: ВК – медиана, высота.
Доказательство:
Т.К. АВК = ВСК , то АК =КС, ∟3 =∟4,
Т.к. АК =КС то К – середина АС, т.е. ВК –медиана.
Т.к. ∟3 =∟4 и смежные, то 180˚ : 2 = 90 ˚ значит ВК – высота.
3
4
ТЕОРЕМА 1.
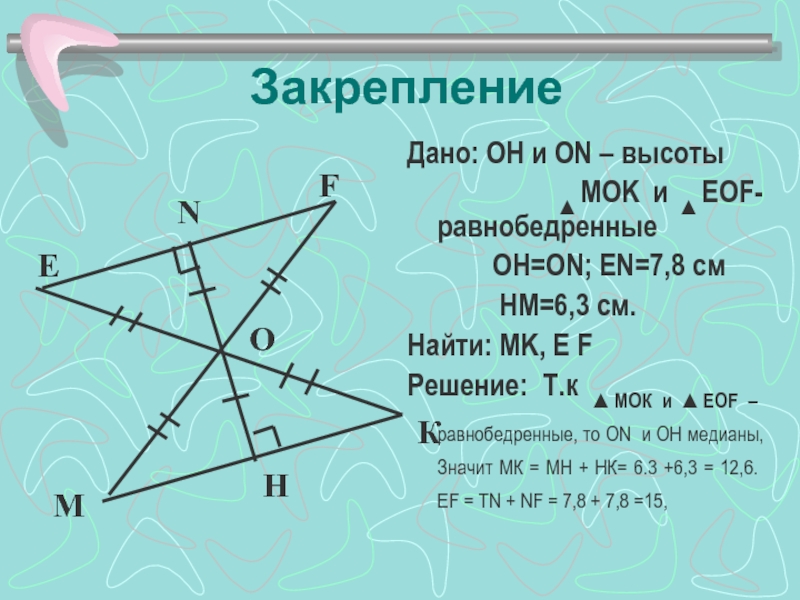
Слайд 14Закрепление
Дано: ОH и ON – высоты
ОH=ОN; EN=7,8 см
HM=6,3 см.
Найти: MK, Е F
Решение: Т.к ▲МОК и ▲ЕОF –равнобедренные, то ОN и OH медианы, Значит МК = МН + НК= 6.3 +6,3 = 12,6. ЕF = TN + NF = 7,8 + 7,8 =15,
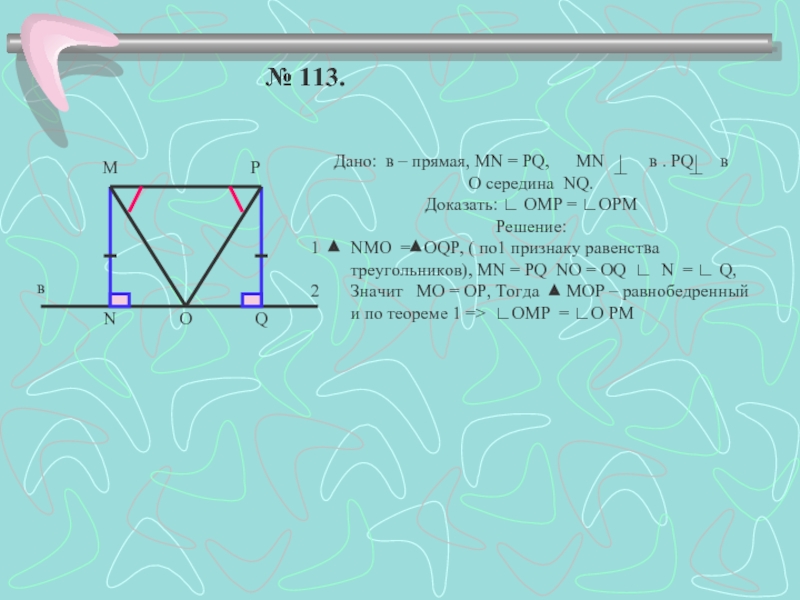
Слайд 15№ 113.
в
М
Р
О
N
Q
Дано: в – прямая, МN = PQ, MN
О середина NQ.
Доказать: ∟ ОМР = ∟ОРМ
Решение:
NMO = OQP, ( по1 признаку равенства треугольников), MN = PQ NO = OQ ∟ N = ∟ Q,
Значит МО = ОР, Тогда МОР – равнобедренный и по теореме 1 => ∟ОМР = ∟О РМ
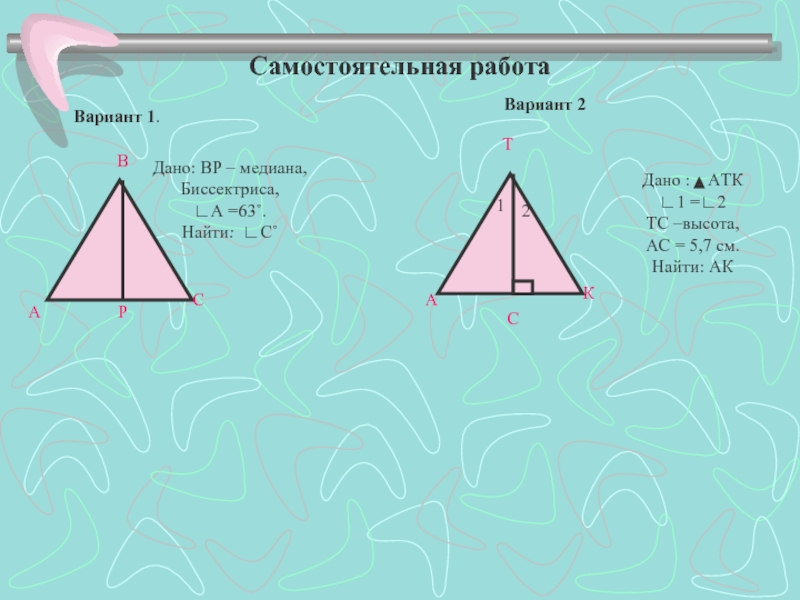
Слайд 16Самостоятельная работа
Вариант 1.
А
В
С
Р
Дано: ВР – медиана,
Биссектриса,
∟А =63˚.
Найти: ∟С˚
А
С
К
Т
1
2
Вариант 2
Дано :
∟1 =∟2
ТС –высота,
АС = 5,7 см.
Найти: АК