Краскела-Уоллиса
16.2. Двухфакторный непараметрический анализ. Критерий Фридмана
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 16. Непараметрические критерии. Факторный анализ. презентация
Содержание
- 1. Тема 16. Непараметрические критерии. Факторный анализ.
- 2. Параметрические и непараметрические критерии Такие статистические критерии,
- 3. 16.1. Критерий Краскела-Уоллиса Kruskal-Wallis Test
- 4. Пример данных Имеется ли разница в среднем
- 5. Критерий Краскела-Уоллиса В дисперсионном анализе используется F-критерий,
- 6. Условия применения Выборки независимы и получены случайным
- 7. Суть критерия 1. В критерии Краскела–Уоллиса все
- 8. Вычисления в таблице
- 9. Критическая область Критерий использует правостороннюю критическую область.
- 10. Статистика Формула статистики Краскела-Уоллиса: где:
- 11. Вычисляем значение статистики
- 12. Находим границу критической области Снова воспользуемся таблицами
- 13. Сравниваем и делаем вывод Полученное значение статистики
- 14. Находим в SPSS Kruskal-Wallis Test Значение
- 15. Статистика – вторая формула Формула статистики Краскела-Уоллиса:
- 16. Вычисления в таблице Ранжируем выборки от 1
- 17. Вычисляем значение статистики Очевидно, мы получили то же самое значение статистики H.
- 18. 16.2. Критерий Джонкхиера Jonckheere Test
- 19. Критерий Джонкхиера Не изучаем! Ура!
- 20. 16.3. Критерий Фридмана Friedman Test
- 21. Факторы A и B На результаты наблюдений
- 22. Таблица двухфакторного анализа Фактор А имеет n
- 23. Модель двухфакторного анализа Результат наблюдения является суммой
- 24. Гипотезы Проверяемая гипотеза: H0: влияние фактора A
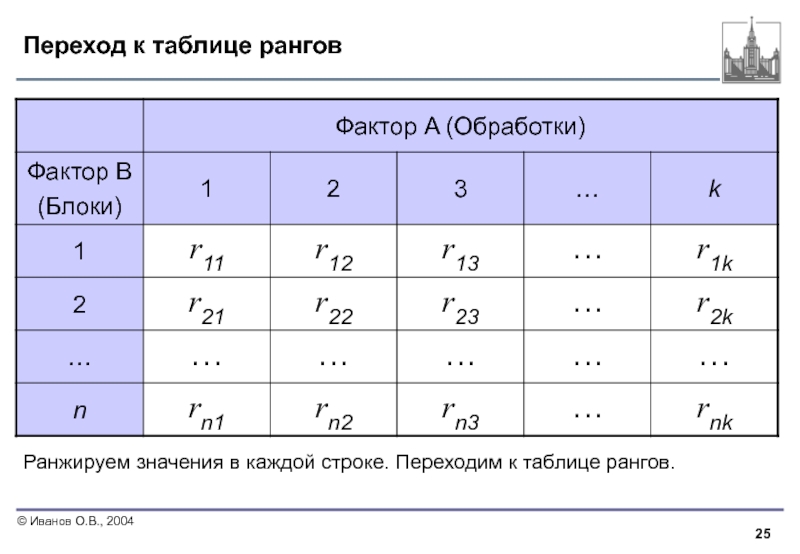
- 25. Переход к таблице рангов Ранжируем значения в каждой строке. Переходим к таблице рангов.
- 26. Суть критерия При ранжировании результатов наблюдений по
- 27. Статистика Фридмана Формула статистики Фридмана:
- 28. Статистика Фридмана – вторая формула Формула статистики
- 29. Пример На уровне α=0,05 проверить влияние каждого из факторов на результаты измерений.
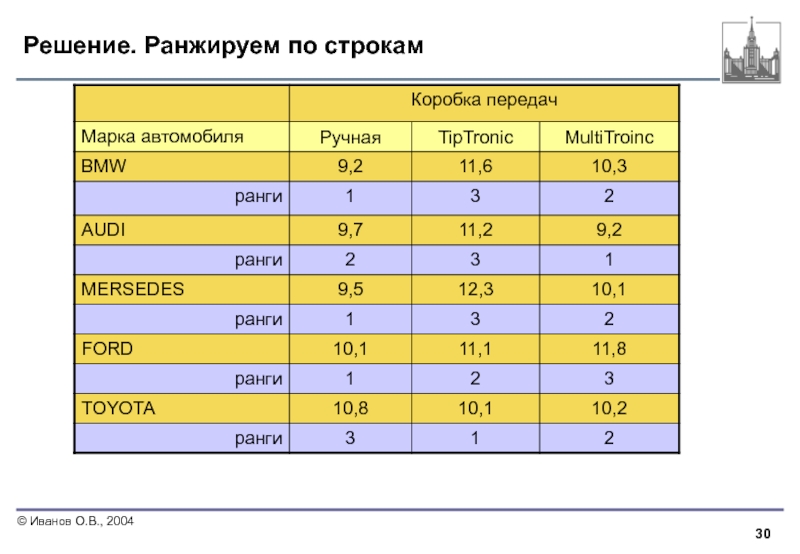
- 30. Решение. Ранжируем по строкам
- 31. Хорошо ли перемешаны ранги?
- 32. Находим средние ранги по столбцам
- 33. Хорошо ли перемешаны ранги? Это покажет критерий!
- 34. Вычисляем статистику
- 35. Считаем в SPSS Критическое значение равно 5,99.
- 36. Вторая проверка Критерий Фридмана используется для второй
- 37. Решение. Ранжируем по столбцам
- 38. Решение. Ранжируем по столбцам Далее как обычно
- 39. 17. Как проводить исследование Классификация методов курса
- 40. Выбор метода Какой тип данных? Интервальные
- 41. 1.1. Интервальные данные, одна совокупность 1.1. Одна
- 42. 1.1. Интервальные данные, одна совокупность 1.1. Одна
- 43. 1.2. Интервальные данные, две совокупности 1.2. Две совокупности Средние Дисперсии Корреляция, регрессия
- 44. 1.2. Интервальные данные, две совокупности 1.2. Две
- 45. Порядковые данные Порядковые данные 2.2. Одна
- 46. Порядковые данные Порядковые данные 2.2. Одна
- 47. Номинальные данные Номинальные данные 3.1. Таблицы сопряженности 3.2. Доли признака Две совокупности Одна совокупность
- 48. Номинальные данные Номинальные данные 3.1. Таблицы
- 49. Понятия и термины
- 50. Задание на 5 минут Чем коэффициент Спирмена отличается от коэффициента Пирсона?
- 51. Задачи 16-1. Измеряется самооценка в трех
- 52. Задачи 16-2. Крупный овощной магазин решает начать
- 53. Задачи 16-3. Клубнику выращивают на трех различных
- 54. Задачи 16-4. Недавно проведенное исследование установило количество
Параметрические и непараметрические критерии Такие статистические критерии, как z, t и F называются параметрическими. Параметрические критерии предназначены для проверки гипотез о параметрах генеральной совокупности - среднем, дисперсии, доли; либо гипотез
Слайд 1Тема 16.
Непараметрические критерии. Факторный анализ.
16.1. Однофакторный непараметрический анализ. Критерий
Слайд 2Параметрические и непараметрические критерии
Такие статистические критерии, как z, t и F
называются параметрическими.
Параметрические критерии предназначены для проверки гипотез о параметрах генеральной совокупности - среднем, дисперсии, доли; либо гипотез о типе распределения.
Кроме этого, статистики разработали направление, которое развивает непараметрические критерии. В этом случае вид и параметры распределения не рассматриваются. Эти критерии используют, в частности, для исследования генеральных совокупностей, которые не распределены нормально.
Параметрические критерии предназначены для проверки гипотез о параметрах генеральной совокупности - среднем, дисперсии, доли; либо гипотез о типе распределения.
Кроме этого, статистики разработали направление, которое развивает непараметрические критерии. В этом случае вид и параметры распределения не рассматриваются. Эти критерии используют, в частности, для исследования генеральных совокупностей, которые не распределены нормально.
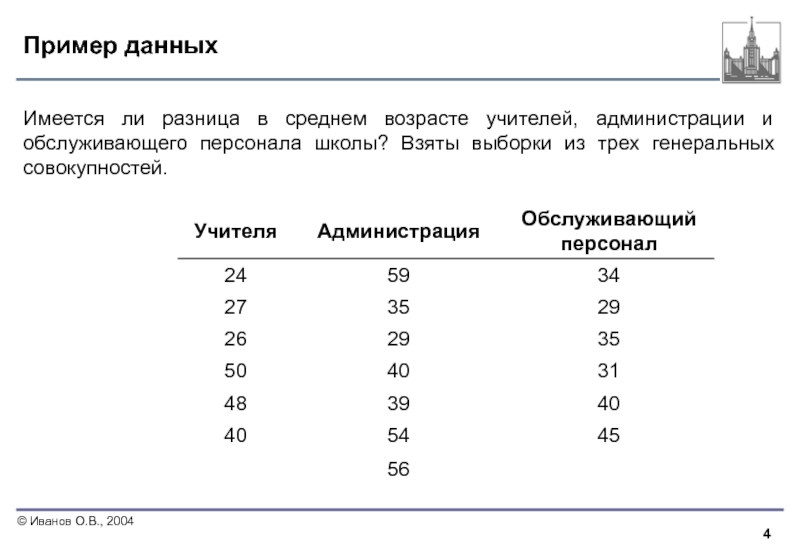
Слайд 4Пример данных
Имеется ли разница в среднем возрасте учителей, администрации и обслуживающего
персонала школы? Взяты выборки из трех генеральных совокупностей.
Слайд 5Критерий Краскела-Уоллиса
В дисперсионном анализе используется F-критерий, чтобы сравнивать средние трех и
более совокупностей. Для критерия ANOVA предполагается, что совокупности нормально распределены и что дисперсии совокупностей равны. Когда эти условия не выполняются, то для сравнения трех и более средних может использоваться непараметрический критерий Краскeла–Уоллиса.
Критерий Краскела-Уоллиса – непараметрический тест, который использует ранги трех и более независимых выборок. Применяется для проверки гипотезы о том, что выборки получены из генеральных совокупностей, имеющих одинаковый закон распределения:
H0: распределения генеральных совокупностей совпадают
H1: распределения отличаются
Критерий Краскела-Уоллиса – непараметрический тест, который использует ранги трех и более независимых выборок. Применяется для проверки гипотезы о том, что выборки получены из генеральных совокупностей, имеющих одинаковый закон распределения:
H0: распределения генеральных совокупностей совпадают
H1: распределения отличаются
Слайд 6Условия применения
Выборки независимы и получены случайным образом.
Размер каждой выборки должен быть
не меньше пяти. В этом случае исследуемое распределение приближается к χ2-распределению с (k – 1) степенями свободы, где k – число градаций признака.
Для выборок меньшего размера требуются специальные таблицы.
Нет ограничений на то, что генеральная совокупность имеет нормальный закон распределения или любой иной определенный закон.
Для выборок меньшего размера требуются специальные таблицы.
Нет ограничений на то, что генеральная совокупность имеет нормальный закон распределения или любой иной определенный закон.
Слайд 7Суть критерия
1. В критерии Краскела–Уоллиса все выборки перемешиваются и значения ранжируются.
Далее вычисляются средние ранги для каждой выборки и средний ранг по всем данным.
2. Если выборки взяты из различных совокупностей, средние ранги выборок будут сильно различаться, значение Н будет велико, нулевая гипотеза будет отвергнута.
3. Для двух выборок критерий совпадает с критерием Вилкоксона.
2. Если выборки взяты из различных совокупностей, средние ранги выборок будут сильно различаться, значение Н будет велико, нулевая гипотеза будет отвергнута.
3. Для двух выборок критерий совпадает с критерием Вилкоксона.
Слайд 9Критическая область
Критерий использует правостороннюю критическую область.
Для нахождения критических значений используем
таблицу χ2-распределения с количеством степеней свободы df = (k – 1).
χ2(α; k -1)
Слайд 10Статистика
Формула статистики Краскела-Уоллиса:
где: – средние ранги выборок (i = 1,2,3,…,k)
– средний ранг по всем выборкам:
– объемы выборок
– объемы выборок
Слайд 12Находим границу критической области
Снова воспользуемся таблицами EXCEL для нахождения границы критической
области:
ХИ2ОБР (0,05; 2) = 5,991
ХИ2ОБР (0,05; 2) = 5,991
Слайд 13Сравниваем и делаем вывод
Полученное значение статистики не попало в критическую область:
Вывод.
Мы не имеем оснований отклонить основную гипотезу. Значит, не существует значимого различия между выборками.
5,991
2,602
Слайд 14Находим в SPSS
Kruskal-Wallis Test
Значение критерия
Имеется небольшое отличие от вычисленного нами вручную
2,602
Слайд 15Статистика – вторая формула
Формула статистики Краскела-Уоллиса:
где: Ri – сумма рангов
i-ой выборки (i = 1,2,3,…,k)
ni – размер i-ой выборки
k – количество уровней фактора
ni – размер i-ой выборки
k – количество уровней фактора
Слайд 16Вычисления в таблице
Ранжируем выборки от 1 до 19 и затем суммируем
ранги каждой выборки отдельно.
Слайд 21Факторы A и B
На результаты наблюдений могут оказывать два и более
факторов.
Рассмотрим двухфакторную модель.
Будем считать, что:
A – главный фактор
B – мешающий фактор
Уровни основного фактора – обработки
уровни мешающего фактора – блоки
Влияние основного фактора – эффекты обработки
Влияние мешающего фактора – эффекты блоков
Рассмотрим двухфакторную модель.
Будем считать, что:
A – главный фактор
B – мешающий фактор
Уровни основного фактора – обработки
уровни мешающего фактора – блоки
Влияние основного фактора – эффекты обработки
Влияние мешающего фактора – эффекты блоков
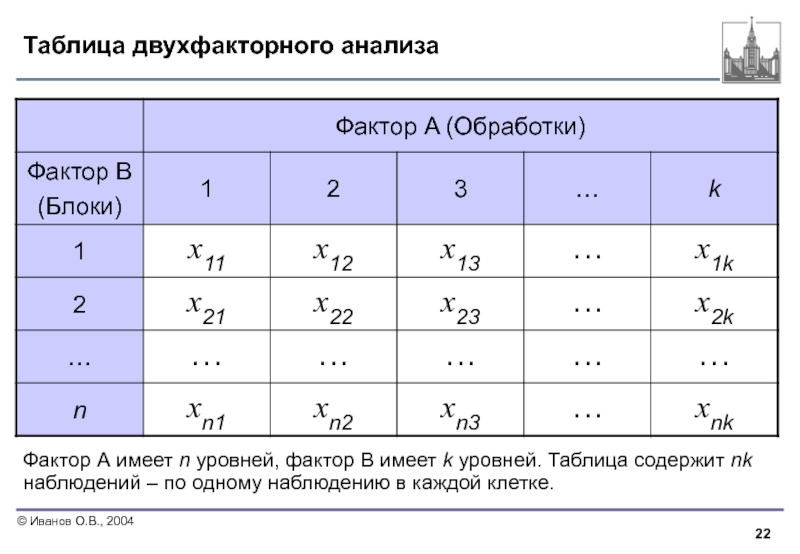
Слайд 22Таблица двухфакторного анализа
Фактор А имеет n уровней, фактор В имеет k
уровней. Таблица содержит nk наблюдений – по одному наблюдению в каждой клетке.
Слайд 23Модель двухфакторного анализа
Результат наблюдения является суммой самостоятельных вкладов соответствующих уровней каждого
фактора и случайности эксперимента:
Влияние фактора B
Влияние фактора A
Среднее
Влияние случайности
Слайд 24Гипотезы
Проверяемая гипотеза:
H0: влияние фактора A отсутствует
H1: влияние фактора имеется
В другой формулировке:
H0:
α1 = α2 = … = αk = 0
H1: не все αi равны нулю
H1: не все αi равны нулю
Слайд 26Суть критерия
При ранжировании результатов наблюдений по строкам, мы устраняем влияние мешающего
фактора В, значение которого для каждой строки таблицы постоянно.
Если гипотеза верна и воздействие фактора А отсутствует, то любая последовательность рангов в строке одинаково вероятна.
Если гипотеза верна и воздействие фактора А отсутствует, то любая последовательность рангов в строке одинаково вероятна.
Слайд 27Статистика Фридмана
Формула статистики Фридмана:
где: – средние ранги по столбцу (i
= 1,2,3,…,k)
– средний ранг по таблице рангов:
– средний ранг по таблице рангов:
Слайд 35Считаем в SPSS
Критическое значение равно 5,99.
Это означает, что нет оснований отвергать
основную гипотезу.
Мы получили, что такой фактор как «тип коробки передач» не оказывает существенного влияния на время разгона автомобилей.
Задача составлена в учебных целях.
Данные взяты «с потолка».
Мы получили, что такой фактор как «тип коробки передач» не оказывает существенного влияния на время разгона автомобилей.
Задача составлена в учебных целях.
Данные взяты «с потолка».
Friedman Test
Слайд 36Вторая проверка
Критерий Фридмана используется для второй проверки. В этом случае, мы
считаем уже, что:
A – мешающий фактор
B – главный фактор
Ранжирование приводим по столбцам, чтобы устранить влияние мешающего фактора.
A – мешающий фактор
B – главный фактор
Ранжирование приводим по столбцам, чтобы устранить влияние мешающего фактора.
Слайд 40Выбор метода
Какой тип
данных?
Интервальные
данные
Порядковые
данные
Номинальные
данные
1.1. Одна совокупность
1.2. Две совокупности
1.3.
Более двух
2.2. Одна совокупность
2.3. Две совокупности
2.4. Более двух
3.1. Таблицы сопряженности
3.2. Доли признака
Слайд 411.1. Интервальные данные, одна совокупность
1.1. Одна совокупность
Среднее
Дисперсия
Доверительный
интервал
Проверка
гипотезы
Доверительный
интервал
Проверка
гипотезы
Слайд 421.1. Интервальные данные, одна совокупность
1.1. Одна совокупность
Среднее
Дисперсия
Доверительный
интервал
Проверка
гипотезы
Доверительный
интервал
Проверка
гипотезы
8.2.
8.4.
9.1.
9.4.
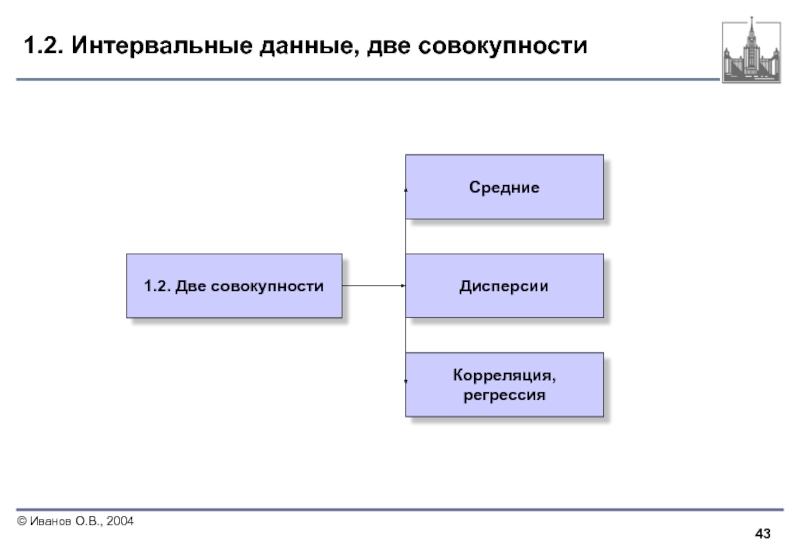
Слайд 431.2. Интервальные данные, две совокупности
1.2. Две совокупности
Средние
Дисперсии
Корреляция,
регрессия
Слайд 441.2. Интервальные данные, две совокупности
1.2. Две совокупности
Средние
Дисперсии
Корреляция,
регрессия
10.1-4.
10.5.
12.1-3.
Слайд 45Порядковые данные
Порядковые
данные
2.2. Одна совокупность
2.3. Две совокупности
2.4. Более двух
Независимые выборки
Парные
выборки
Слайд 46Порядковые данные
Порядковые
данные
2.2. Одна совокупность
2.3. Две совокупности
2.4. Более двух
Независимые выборки
Парные
выборки
16.1.
14.1.
14.3-4.
14.1-2.
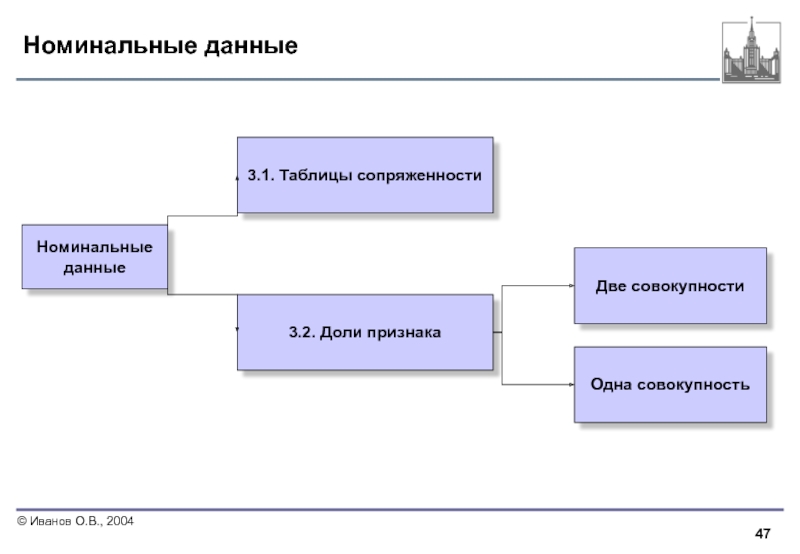
Слайд 47Номинальные данные
Номинальные
данные
3.1. Таблицы сопряженности
3.2. Доли признака
Две совокупности
Одна совокупность
Слайд 48Номинальные данные
Номинальные
данные
3.1. Таблицы сопряженности
3.2. Доли признака
Две совокупности
Одна совокупность
8.3.
9.3.
10.6-7.
11.3.
Слайд 51Задачи
16-1. Измеряется самооценка в трех различных выборках индивидов по порядку
рождения. Количество набранных баллов ранжируется от 0 до 50. Существует ли разница в количестве набранных баллов на уровне значимости α = 0,05?
Слайд 52Задачи
16-2. Крупный овощной магазин решает начать рекламировать продукт тремя различными способами:
по радио, по телевидению, в газетах. По результатам продаж в течение одной недели в случайно выбранных магазинах были получены следующие данные. Существует ли разница в продажах в связи с типом рекламирования товара на уровне значимости α = 0,01?
Слайд 53Задачи
16-3. Клубнику выращивают на трех различных типах почвы. Урожай (в квартах)
на одинаковых участках представлен ниже. Существует ли различие в количестве урожая для трех участков на уровне значимости α = 0,01?
Слайд 54Задачи
16-4. Недавно проведенное исследование установило количество предложений о работе, принимаемых выпускниками
инженерами-химиками в трех различных колледжах. Существует ли на уровне значимости α = 0,01 различие между средним количеством принятых предложений о работе в этих колледжах ?
