- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сущность Полевой физикиПолевая механикаРепченко Олег Николаевичwww.fieldphysics.ru презентация
Содержание
- 1. Сущность Полевой физикиПолевая механикаРепченко Олег Николаевичwww.fieldphysics.ru
- 2. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Классическая
- 3. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Согласно
- 4. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Возмущение
- 5. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Полевая
- 6. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В
- 7. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Реализация
- 8. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Из
- 9. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В
- 10. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В
- 11. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В
- 12. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Для
- 13. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Классическая
- 14. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Релятивистская
- 15. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Галактическое
- 16. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Принцип
- 17. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Следствия
- 18. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Другие
- 19. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Обобщенное
- 20. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Обобщенное
- 21. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Модель
- 22. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Из
- 23. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Согласно
Слайд 2© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Классическая теория поля рассматривает физические поля
Слайд 3© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Согласно полевой физике объекты не создают
Слайд 4© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Возмущение полевой среды объектами и передача
Слайд 5© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Полевая среда описывается функцией плотности W(r,
Слайд 6© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
В самом элементарном случае (взаимодействие только
Слайд 7© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Реализация указанного механизма полевого взаимодействия двух
W(R) – функция полевой связи объектов
u – их относительная скорость
R – их относительное расстояние
c – скорость света
Слайд 8© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Из полевого уравнению движения следуют:
Формула полевой
А уравнение движения принимает вид:
Слайд 9© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
В наиболее простом случае функция полевой
Его решение:
Константа является еще одной из характеристик полевой среды, называемой интенсивностью. Она соответствует понятию заряда q или произведения зарядов qQ взаимодействующих объектов.
Слайд 10© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
В полевой физике равноправным образом возникает
где ϕe и ϕg − соответственно потенциал электрического и гравитационного поля.
Слайд 11© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
В земных условиях вклад в инертную
Такова природа принципа эквивалентности, наблюдаемого в земных условиях.
Слайд 12© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Для описания движения в реальных условиях
Слайд 13© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
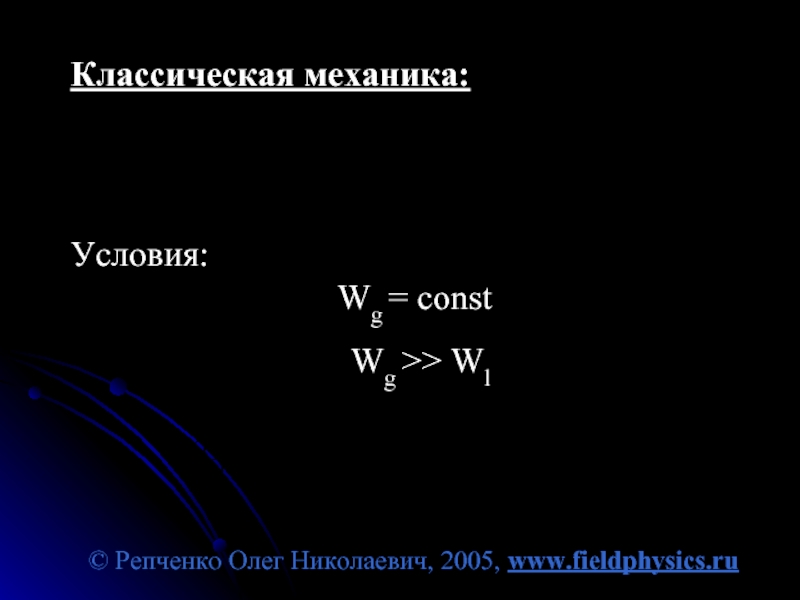
Классическая механика:
Условия:
Слайд 14© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Релятивистская механика:
Условия:
Слайд 15© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Галактическое движение:
Условия:
Слайд 16© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Принцип инерции Галилея:
При отсутствии внешних сил
Слайд 17© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Следствия ПФ в космологии:
− Объяснение структуры
Слайд 18© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Другие следствия Полевой физики:
− Механизм возникновения
Слайд 19© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Обобщенное полевое уравнение движения:
u – скорость
Слайд 20© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Обобщенное полевое уравнение движения справедливо в
Совокупность слагаемых:
описывает как любые механические, так и полевые силы инерции.
Слайд 21© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Модель инерциальной СО является частным случаем,
Инерциальные СО существуют только в простых задачах. Когда объектов много и они движутся неодинаково, то инерциальной СО не существует в принципе.
Слайд 22© Репченко Олег Николаевич, 2005, www.fieldphysics.ru
Из обобщенного уравнения движения следует скорректированное