- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ презентация
Содержание
- 1. СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ
- 2. Статистический показатель Это количественная характеристика социально-экономического
- 3. Статистический показатель Абсолютные Относительные Средние
- 4. Абсолютный показатель отражает физические размеры изучаемого
- 5. Абсолютный показатель Натуральные Стоимостные Трудовые Индивидуальные Суммарный Моментный Интервальный
- 6. Относительный показатель обобщающий показатель,
- 7. Цепной относительный показатель – если база
- 8. Относительный показатель
- 9. Относительный показатель динамики – темп роста
- 14. Относительный показатель выполнения плана и планового задания
- 15. Оборот торговой фирмы в 2002 г. составил
- 16. Относительные величины структуры Характеризуют
- 19. Относительный показатель координации Характеризует
- 22. Относительный показатель сравнения Характеризует
- 25. Относительный показатель интенсивности Характеризует
- 26. На конец 2000 года численность безработных составила 8798,25 тыс.чел.
- 27. Средний показатель обобщающий показатель,
- 28. Средние Степенные Структурные Арифметическая Гармоническая Геометрическая Мода Квадратическая Медиана
- 29. Степенные средние
- 30. Виды степенных средних
- 31. Пример
- 32. Средний возраст Простая средняя Взвешенная средняя
- 33. Структурные средние
- 34. Структурные средние
- 35. Показатели вариации: частотные показатели; показатели распределения
- 36. Частотные показатели вариации абсолютная численность i-той
- 37. Показатели вариации:
- 38. Показатели вариации:
- 39. Дисперсия:
- 40. Показатели относительного рассеивания :
- 41. Пример 1
- 42. Пример 1
- 43. Пример 1
- 44. Пример 1
- 45. Пример 1
- 46. Пример 1
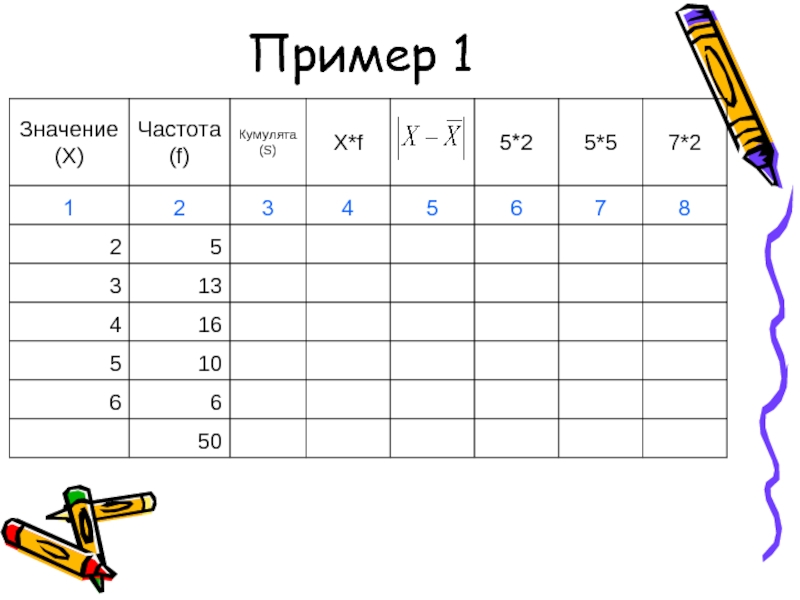
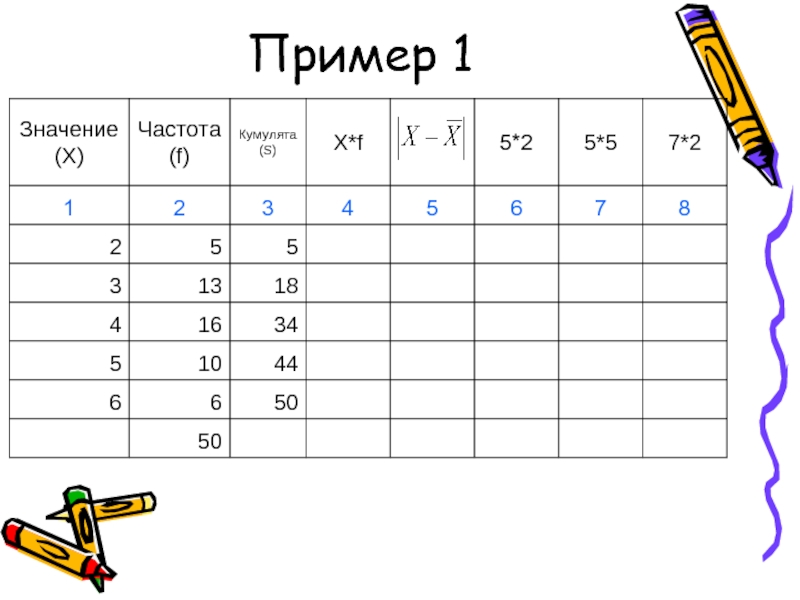
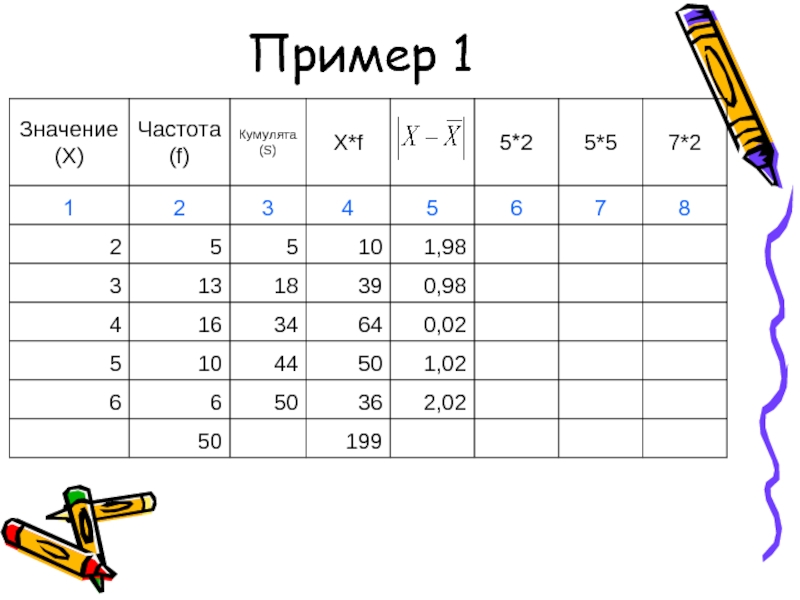
- 47. Пример 1
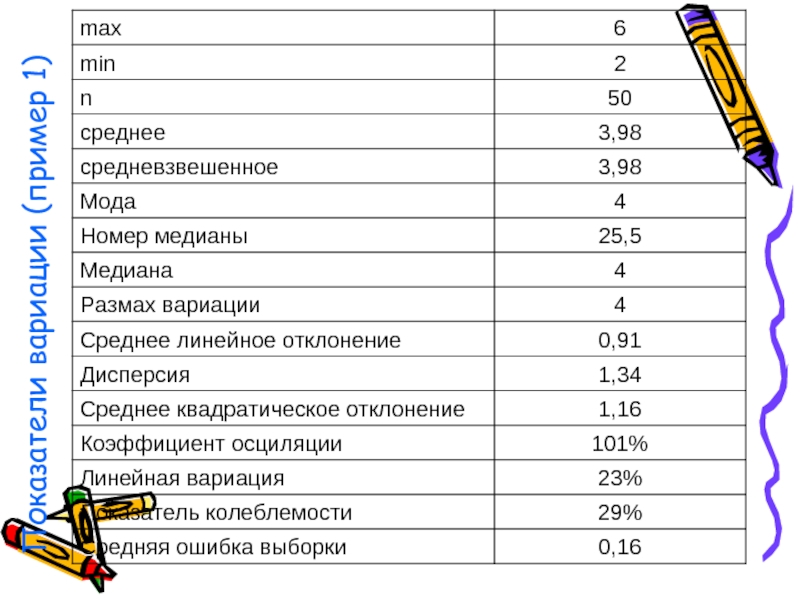
- 48. Показатели вариации (пример 1)
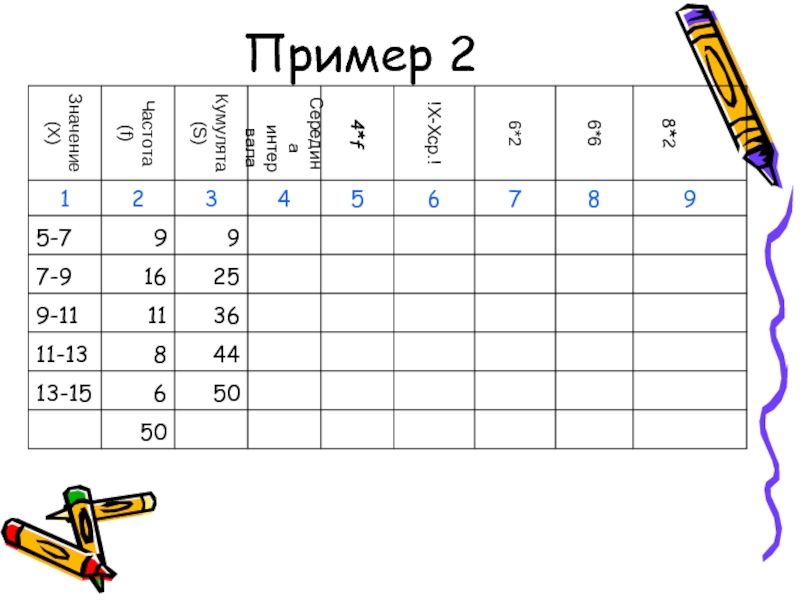
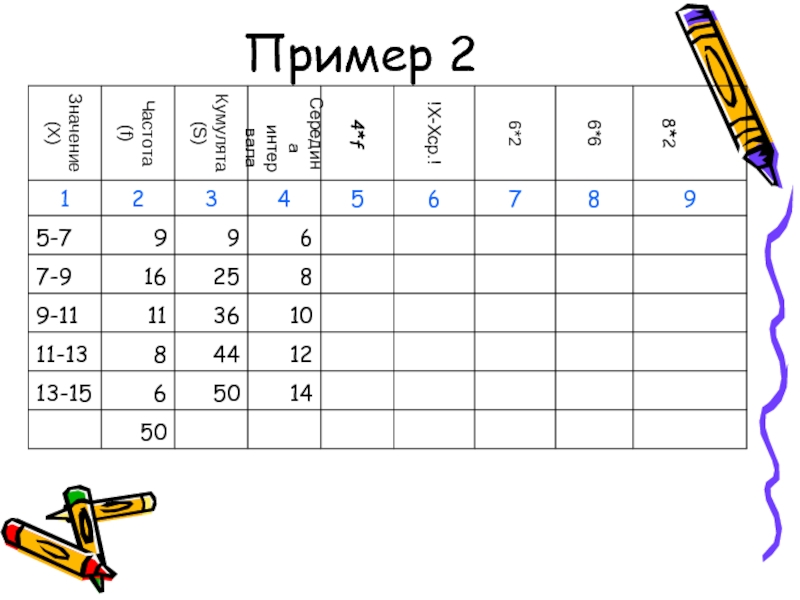
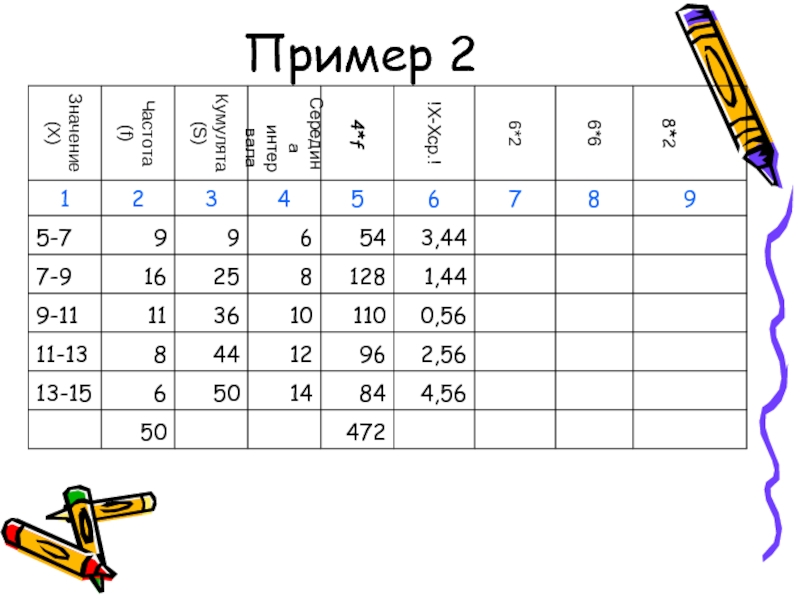
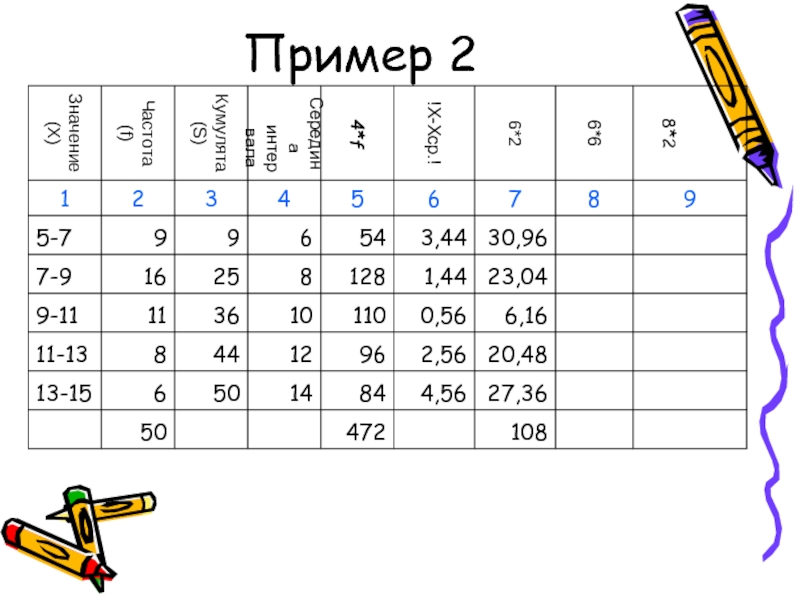
- 49. Пример 2
- 50. Пример 2
- 51. Пример 2
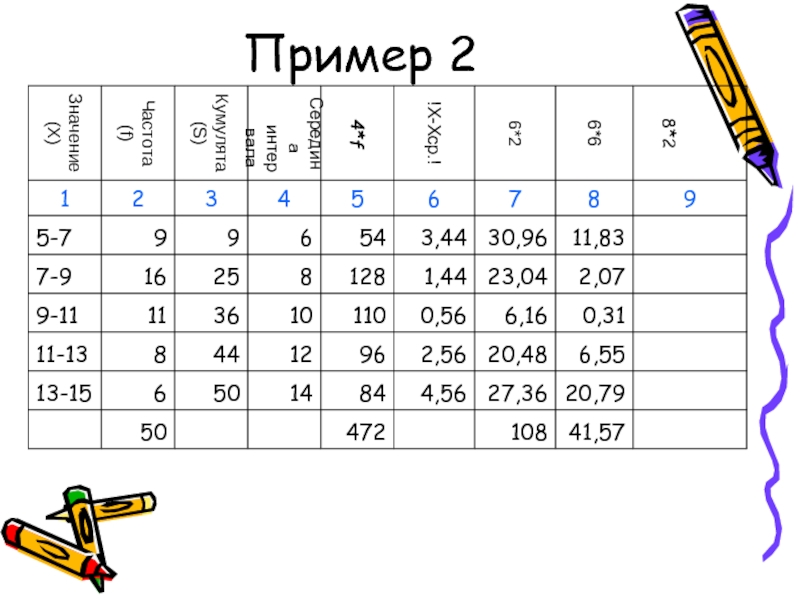
- 52. Пример 2
- 53. Пример 2
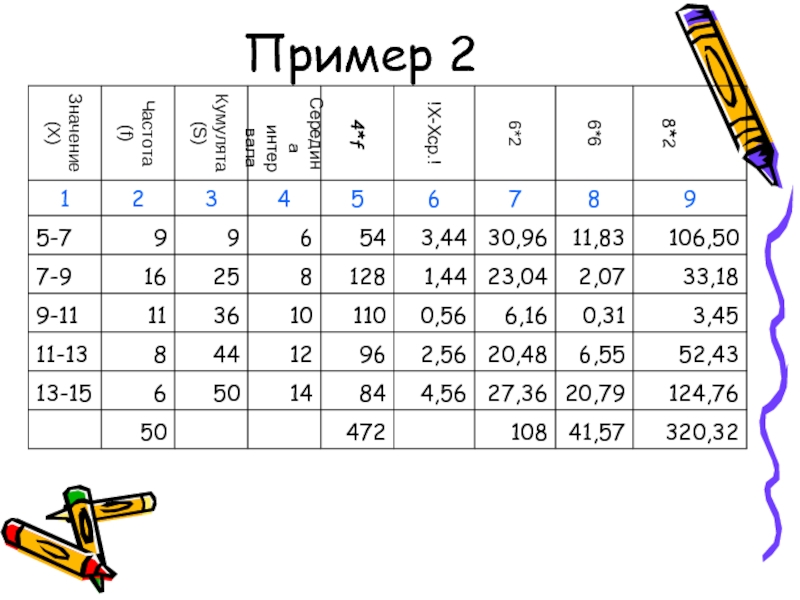
- 54. Пример 2
- 55. Пример 2
- 56. Пример 2
- 57. Показатели вариации (пример 2)
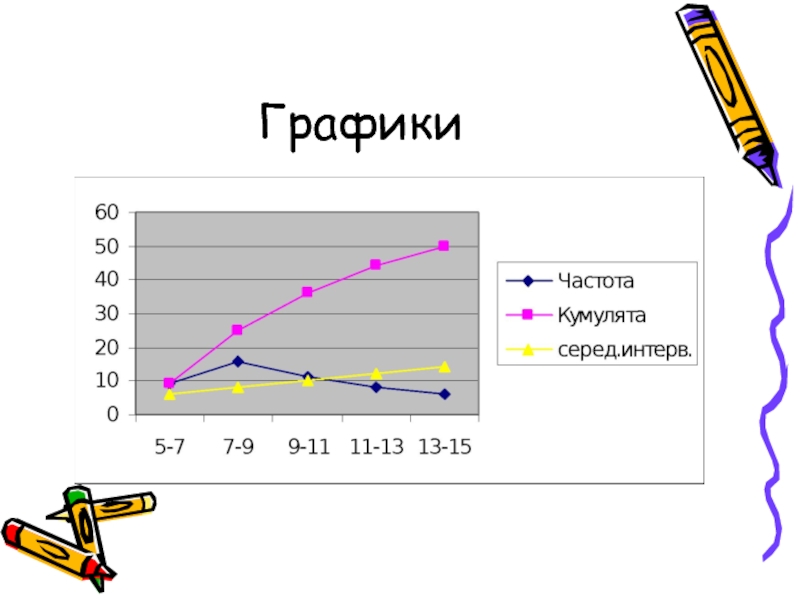
- 58. Графики
- 59. Графическое определение моды Гистограмма Частота (f) Признак (X)
- 60. Графическое определение моды Кумулята Частота (f) Признак
Статистический показатель Это количественная характеристика социально-экономического явления или процесса в условиях качественной определенности. Качественная определенность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса,
Слайд 2Статистический показатель
Это количественная характеристика социально-экономического явления или процесса в условиях
качественной определенности.
Качественная определенность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью.
Количественное значение статистического показателя является его величиной.
Качественная определенность показателя заключается в том, что он непосредственно связан с внутренним содержанием изучаемого явления или процесса, его сущностью.
Количественное значение статистического показателя является его величиной.
Слайд 4Абсолютный показатель
отражает физические размеры изучаемого явления
именованный
измеряются в конкретных единицах
может
быть положительным или отрицательным
Слайд 5Абсолютный показатель
Натуральные
Стоимостные
Трудовые
Индивидуальные
Суммарный
Моментный
Интервальный
Слайд 6Относительный показатель
обобщающий показатель, который дает числовую меру соотношения
двух сопоставляемых абсолютных величин и определяется как результат деления одной абсолютной величины на другую
Слайд 7Цепной относительный показатель –
если база сравнения переменная
Базисный относительный показатель –
если база сравнения постоянная
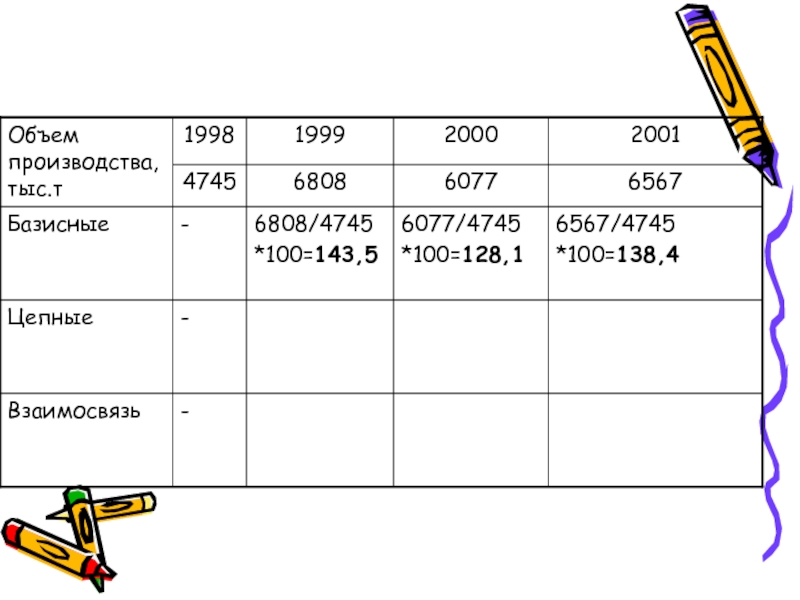
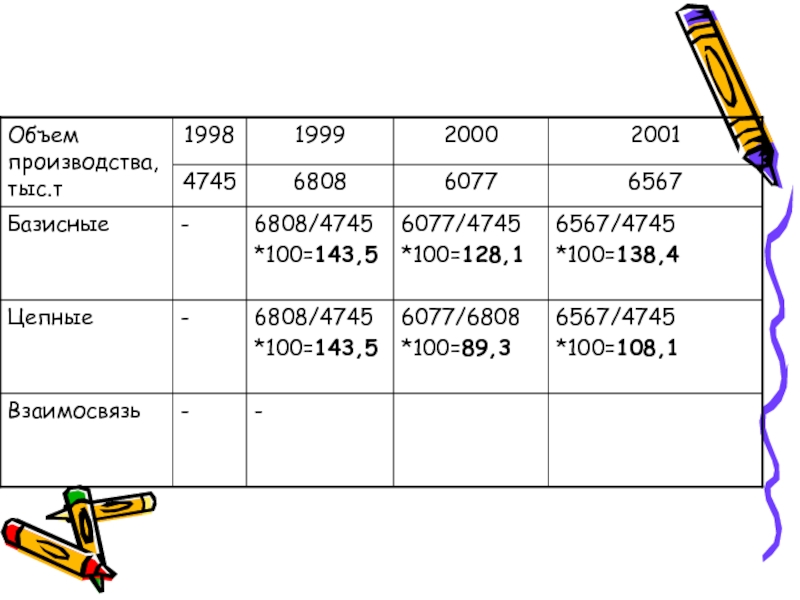
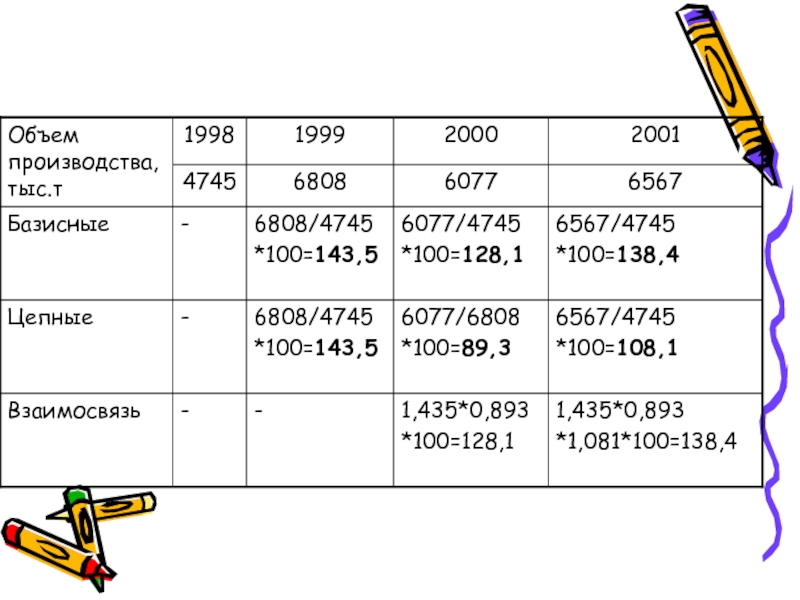
Слайд 9Относительный показатель динамики – темп роста
Характеризует изменение уровня
развития какого-либо явления во времени
Слайд 14Относительный показатель выполнения плана и планового задания
;
.
ОПП*ОПРП=ОПД
относительные
показатели
плана
относительные
показатели
реализации
плана
Взаимосвязь показателей
Слайд 15Оборот торговой фирмы в 2002 г. составил 2,0 млн. руб. На
2003 год запланировано достичь оборота 2,8 млн. руб. Фактически в 2003 г оборот составил 2,6 млн. руб.
;
.
относительные
показатели
плана
относительные
показатели
реализации
плана
ОПП = 2,8 / 2,0 * 100 % = 140 %
ОПРП = 2,6 / 2,8 * 100 % = 92,9 %
ОПД = 1,40 * 0,929 = 2,6 / 2,0 = 1,3 (130 %)
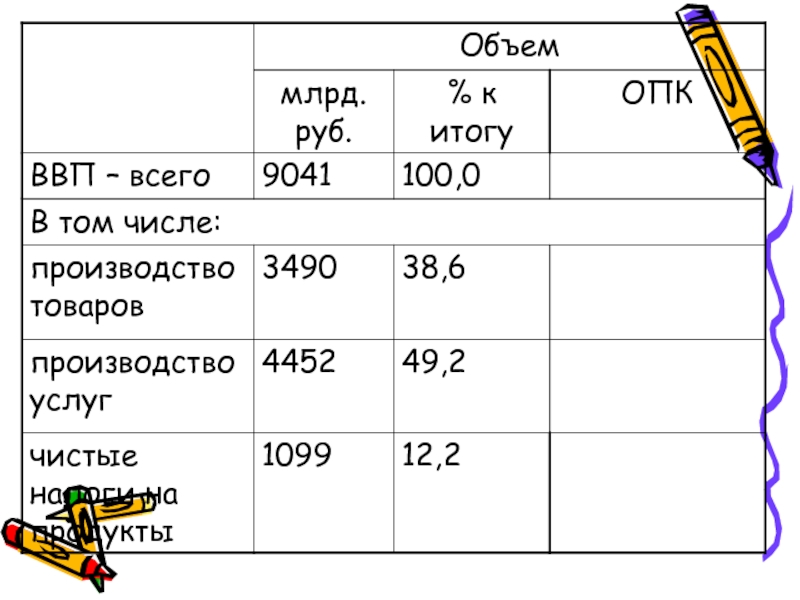
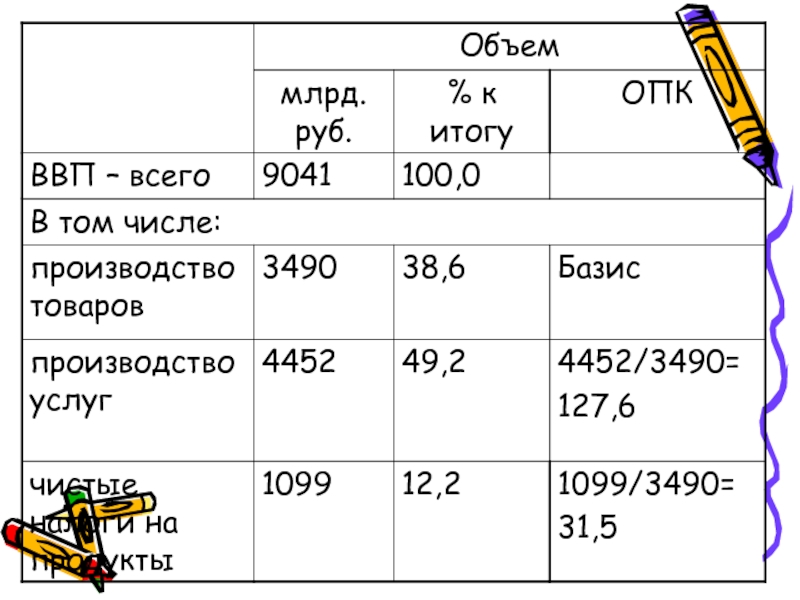
Слайд 16Относительные величины структуры
Характеризуют доли, удельные веса составных элементов
в общем итоге
Слайд 19Относительный показатель координации
Характеризует отношение частей данной совокупности к
одной из них, принятой за базу сравнения
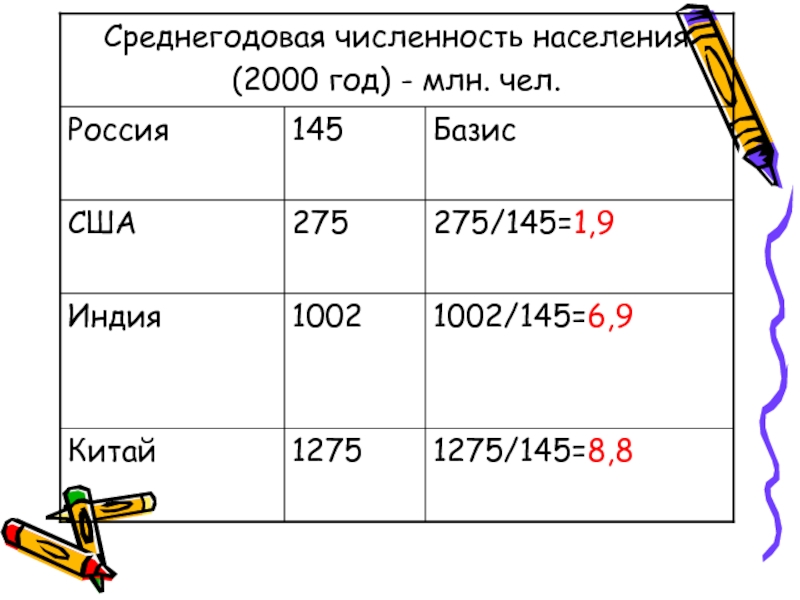
Слайд 22Относительный показатель сравнения
Характеризует сравнительные размеры одноименных абсолютных величин,
относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям
Слайд 25Относительный показатель интенсивности
Характеризует степень распределения или развития данного
явления в той или иной среде
Слайд 28Средние
Степенные
Структурные
Арифметическая
Гармоническая
Геометрическая
Мода
Квадратическая
Медиана
Слайд 29Степенные средние
Простая средняя
где Xi - варианта (значение) осредняемого признака;
m - показатель степени средней;
n - число вариант.
n - число вариант.
Взвешенная средняя
где Xi - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
m - показатель степени средней;
fi - частота, показывающая, сколько раз встречается i-e значение осредняемого признака.
Слайд 33Структурные средние
Мода
наиболее часто повторяющееся значения признака
где ХMo -
нижнее значение модального интервала;
mMo - число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
m Mo-1 - то же для интервала, предшествующего модальному;
m Mo+1 - то же для интервала, следующего за модальным;
h - величина интервала изменения признака в группах
mMo - число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
m Mo-1 - то же для интервала, предшествующего модальному;
m Mo+1 - то же для интервала, следующего за модальным;
h - величина интервала изменения признака в группах
Слайд 34Структурные средние
Медиана
величина признака, которая делит упорядоченную последовательность его значений
на две равные по численности части
где XMe - нижняя граница медианного интервала;
hMe - его величина;
∑m/2- половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
SMe-1 - сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
mMe - число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).
Слайд 35Показатели вариации:
частотные показатели;
показатели распределения – структурные средние;
показатели степени вариации;
показатели формы
распределения.
Слайд 36Частотные показатели вариации
абсолютная численность i-той группы – частота fi
относительная
частота – частость di
кумулятивная (накопленная) частота Si (частость Sd) характеризует объем совокупности со значениями вариантов, не превышающих Xi.
S1=f1, S2=f1+f2, S3=f1+f2+f3;
плотность частоты (частости) представляет собой частоту, приходящуюся на единицу интервала,
qi=fi/hi или qi=di/hi
где hi – величина i-того интервала.
кумулятивная (накопленная) частота Si (частость Sd) характеризует объем совокупности со значениями вариантов, не превышающих Xi.
S1=f1, S2=f1+f2, S3=f1+f2+f3;
плотность частоты (частости) представляет собой частоту, приходящуюся на единицу интервала,
qi=fi/hi или qi=di/hi
где hi – величина i-того интервала.
Слайд 39Дисперсия:
Дисперсия постоянной величины равна 0.
Если все значения вариантов признака
X уменьшить на постоянную величину А, то дисперсия не изменится.
Если все значения вариантов Х уменьшить в К раз, то дисперсия уменьшится в К2 раз.
На практике часто используют более простую формулу для расчета дисперсии:
5.При малом числе наблюдений (< 30):
Если все значения вариантов Х уменьшить в К раз, то дисперсия уменьшится в К2 раз.
На практике часто используют более простую формулу для расчета дисперсии:
5.При малом числе наблюдений (< 30):
