по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременною. На каком расстоянии от более высокой пальмы появилась раба.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
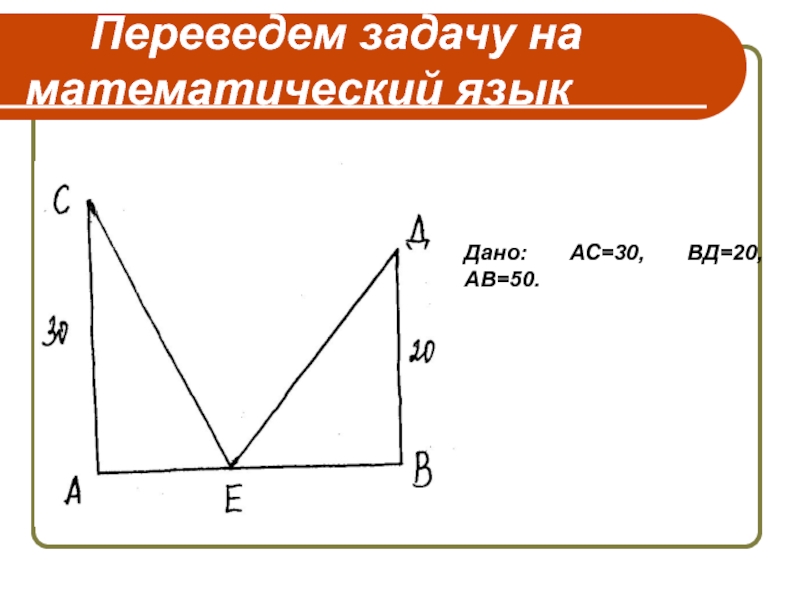
Старинная задача На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями. презентация
Содержание
- 2. Старинная задача
- 3. Переведем задачу на математический язык Дано: АС=30, ВД=20, АВ=50.
- 4. Нужно знать зависимость между катетами и гипотенузой
- 5. Биография Пифагора Пифагор-это не
- 6. Пифагорейская школа Вернувшись на
- 7. Пифагорейская школа
- 8. Заповеди Пифагора
- 9. Заповеди пифагорийцев Делать
- 10. 1.Начертить прямоугольный треугольник.
- 11. 1. Найдите площадь
- 12. Вывод: Площадь квадрата построенного на
- 13. Квадраты построенные на катетах, состоят из
- 14. Теорема Пифагора современная формулировка: «Квадрат гипотенузы равен
- 15. Начертим прямоугольный
- 16. С другой стороны SABCD=4Sтр +Sкв Sтр=
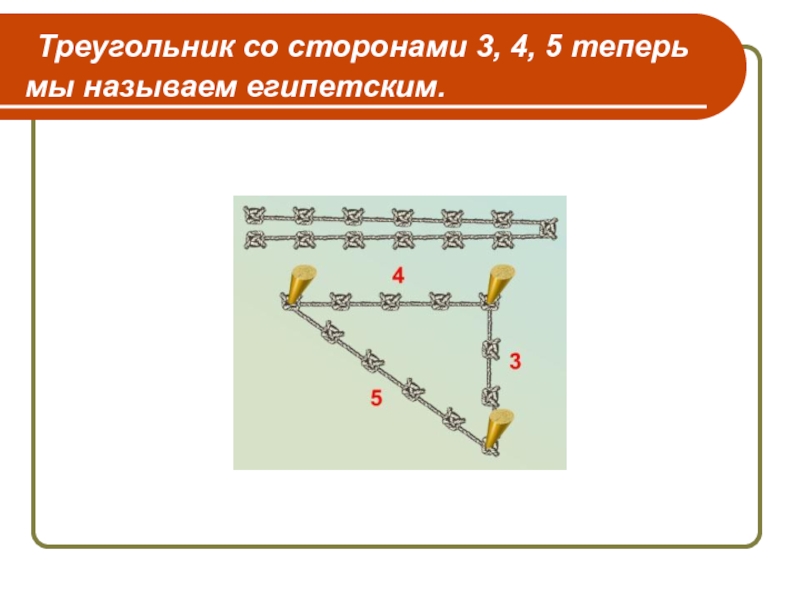
- 17. Треугольник со сторонами 3, 4, 5 теперь мы называем египетским.
- 18. Вам, наверное, известны также детские стишки о
- 19. До нас дошли и другие шуточные рисунки к теореме
- 20. Если дан нам треугольник И притом
- 21. Решить: №483(а,б), №484(а,б) №487
- 22. Домашнее задание П.54, вопрос 8; № 483(в,г); №484(в,г,д); №486(в)
Старинная задача На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой 20 локтей. Расстояние между их основаниями 50 локтей. На
Слайд 4Нужно знать зависимость между катетами и гипотенузой в прямоугольном треугольнике.
Эту зависимость
подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора.
Слайд 5Биография Пифагора
Пифагор-это не имя, а прозвище, данное ему
за
то , что он высказывал истину также постоянно, как дельфийский аракул, («Пифагор» значит «убеждающий речью») жил в Древней Греции. О жизни его известно немного, зато с именем его связан ряд легенд. Рассказывают, что он много путешествовал, изучал древнюю культуру и достижения науки разных стран.
то , что он высказывал истину также постоянно, как дельфийский аракул, («Пифагор» значит «убеждающий речью») жил в Древней Греции. О жизни его известно немного, зато с именем его связан ряд легенд. Рассказывают, что он много путешествовал, изучал древнюю культуру и достижения науки разных стран.
Слайд 6Пифагорейская школа
Вернувшись на родину, Пифагор
организовал кружок молодежи из
представителей аристократии. В
кружок принимались с большими
церемониями после долгих испытаний.
Каждый вступающий отрекался от
своего имущества и давал клятву
хранить в тайне учения основателя.
Так на юге Италии, которая была
тогда греческой колонией, возникла
пифагорейская школа.
представителей аристократии. В
кружок принимались с большими
церемониями после долгих испытаний.
Каждый вступающий отрекался от
своего имущества и давал клятву
хранить в тайне учения основателя.
Так на юге Италии, которая была
тогда греческой колонией, возникла
пифагорейская школа.
Слайд 7Пифагорейская школа
Пифагорейцы занимались
математикой, философией,
естественными науками.
Ими было сделано много важных открытий в арифметике и геометрии.
В школ существовал декрет, по которому авторство всех математических работ
приписывалось Пифагору.
естественными науками.
Ими было сделано много важных открытий в арифметике и геометрии.
В школ существовал декрет, по которому авторство всех математических работ
приписывалось Пифагору.
Звездчатый пятиугольник, или пентаграмма, - пифагорейский символ здравия и тайный опознавательный знак
Слайд 8 Заповеди Пифагора
и его учеников актуальны
и сейчас и могут быть
приемлемы для любого здравомыслящего человека.
Вот они!
приемлемы для любого здравомыслящего человека.
Вот они!
Слайд 9 Заповеди пифагорийцев
Делать то, что впоследствии не огорчит тебя
и не принудит раскаиваться;
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Не делай никогда того, что не знаешь, но научись всему, что следует знать;
Не пренебрегай здоровьем своего тела;
Приучайся жить просто и без роскоши.
Слайд 10
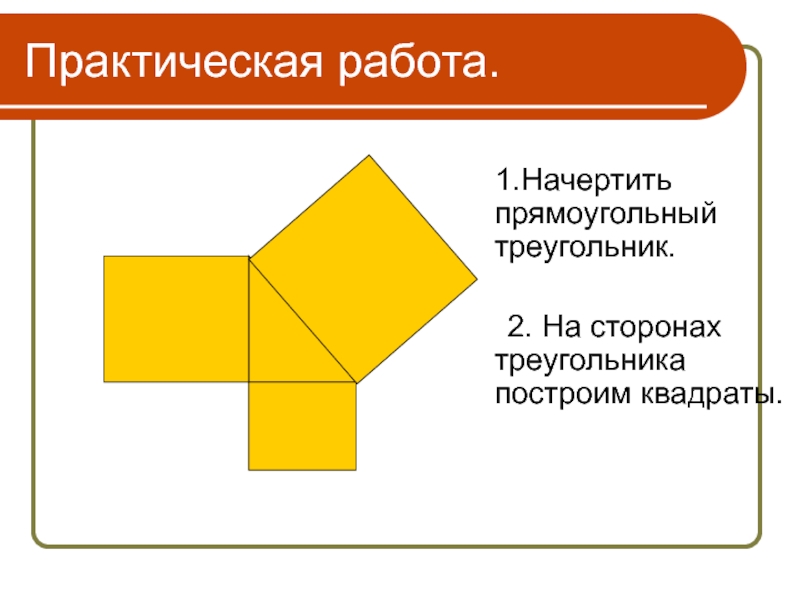
1.Начертить прямоугольный треугольник.
2. На сторонах
треугольника построим квадраты.
Практическая работа.
Слайд 11
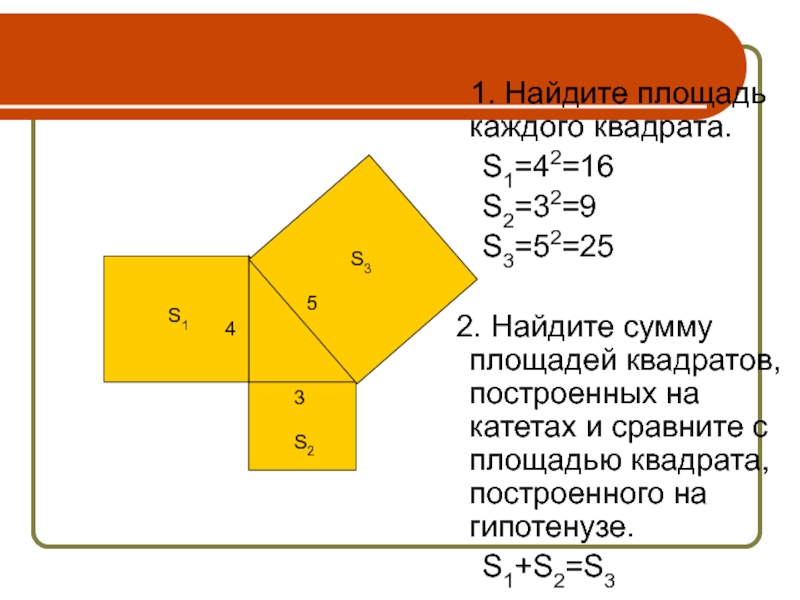
1. Найдите площадь каждого квадрата.
S1=42=16
S2=32=9
S3=52=25
2. Найдите сумму площадей квадратов, построенных на катетах и сравните с площадью квадрата, построенного на гипотенузе.
S1+S2=S3
S2=32=9
S3=52=25
2. Найдите сумму площадей квадратов, построенных на катетах и сравните с площадью квадрата, построенного на гипотенузе.
S1+S2=S3
4
3
5
S1
S3
S2
Слайд 12Вывод:
Площадь квадрата построенного на гипотенузе прямоугольного треугольника равна сумме
площадей квадратов, построенных на катетах.
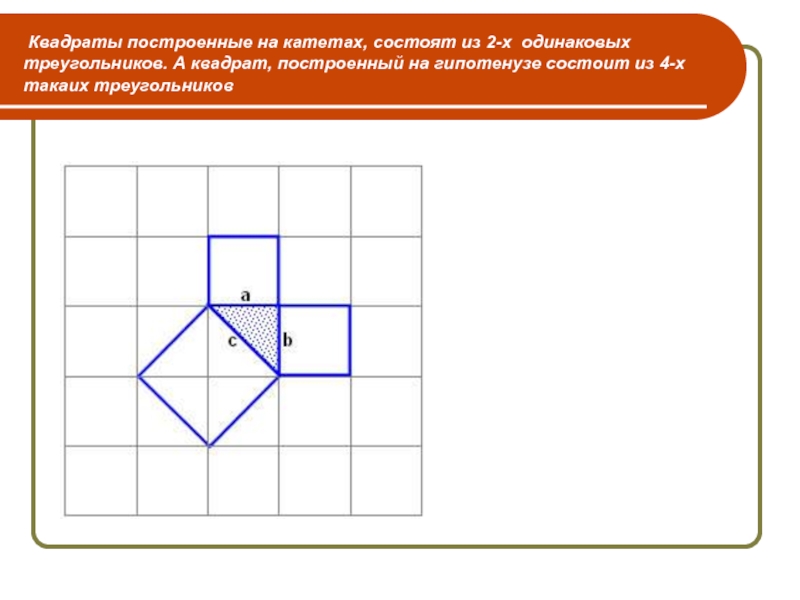
Слайд 13 Квадраты построенные на катетах, состоят из 2-х одинаковых треугольников. А
квадрат, построенный на гипотенузе состоит из 4-х такаих треугольников
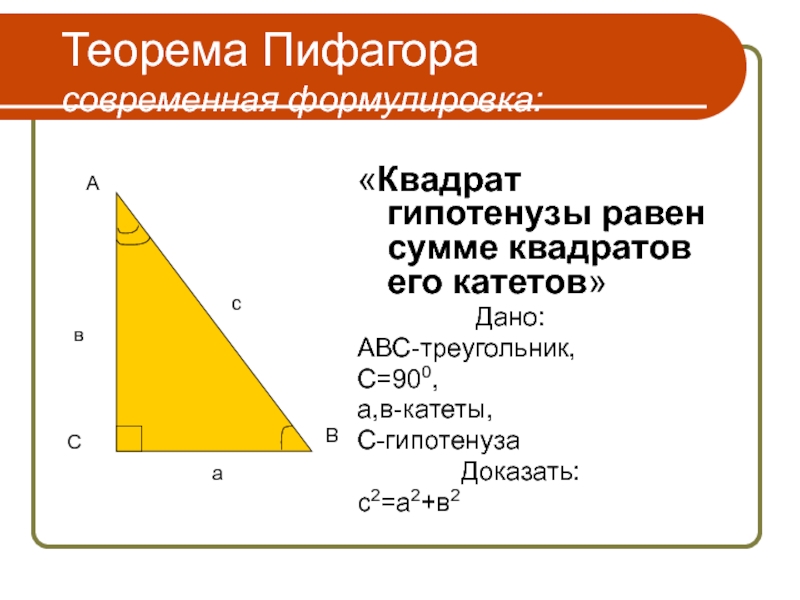
Слайд 14Теорема Пифагора
современная формулировка:
«Квадрат гипотенузы равен сумме квадратов его катетов»
Дано:
АВС-треугольник,
С=900,
а,в-катеты,
С-гипотенуза
Доказать:
с2=а2+в2
АВС-треугольник,
С=900,
а,в-катеты,
С-гипотенуза
Доказать:
с2=а2+в2
А
В
С
с
а
в
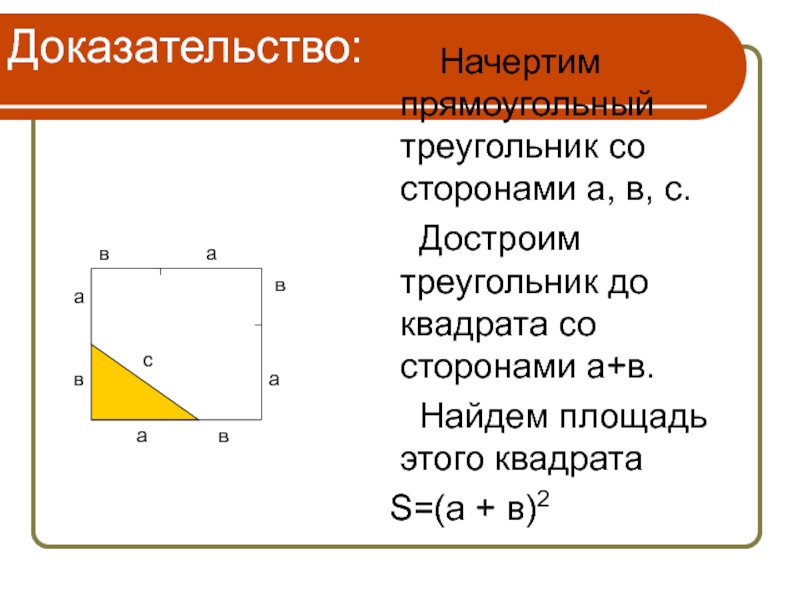
Слайд 15
Начертим прямоугольный треугольник со сторонами а, в,
с.
Достроим треугольник до квадрата со сторонами а+в.
Найдем площадь этого квадрата
S=(а + в)2
Достроим треугольник до квадрата со сторонами а+в.
Найдем площадь этого квадрата
S=(а + в)2
а
с
в
в
в
в
а
а
а
Доказательство:
Слайд 16С другой стороны
SABCD=4Sтр +Sкв
Sтр= ав;
Sкв=c2
SABCD=4* ав+с2=2ав+с2
(а+в)2=2ав+с2
а2+2ав+в2=2ав+с2
а2+в2=с2
ч.т.д.
а
в
с
А
В
С
D
а
а
а
в
в
в
с
с
с
c
c
c
c
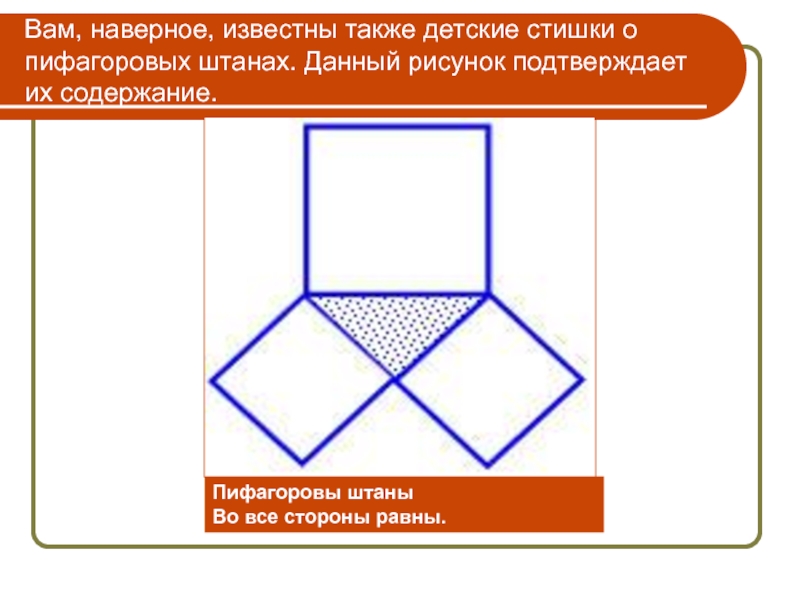
Слайд 18Вам, наверное, известны также детские стишки о пифагоровых штанах. Данный рисунок
подтверждает их содержание.
Пифагоровы штаны
Во все стороны равны.
Слайд 20
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путём
К результату мы придём.
