- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Современные проблемы информатикиЛекция 1ВведениеТранзиционные системы презентация
Содержание
- 1. Современные проблемы информатикиЛекция 1ВведениеТранзиционные системы
- 2. План лекций Теория взаимодействующих процессов (CCS, CSP,
- 3. Теории взаимодействия и параллелизма (communication, interaction and
- 4. Транзиционные системы Ординарные транзиционные (динамические) системы :
- 5. D.Park (1981) Размеченные транзиционные системы А –
- 6. Смешанные системы наблюдаемые переходы скрытые переходы
- 7. Атрибутные транзиционные системы D={0,1} (Не размеченные
- 8. Настроенные системы Другие важные классы транзиционных систем:
- 9. Применения Моделирование поведения и
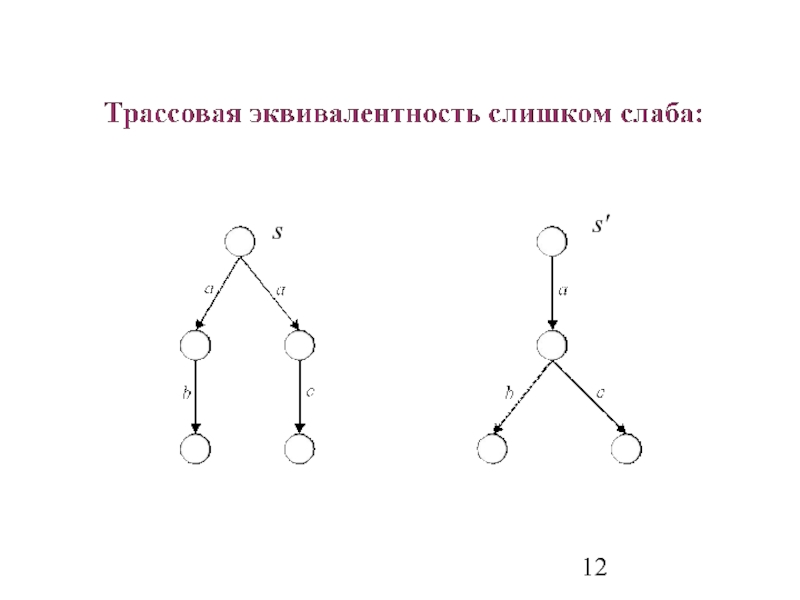
- 10. Трассовая эквивалентность История: Трасса: Трасса для атрибутной системы: трассы из
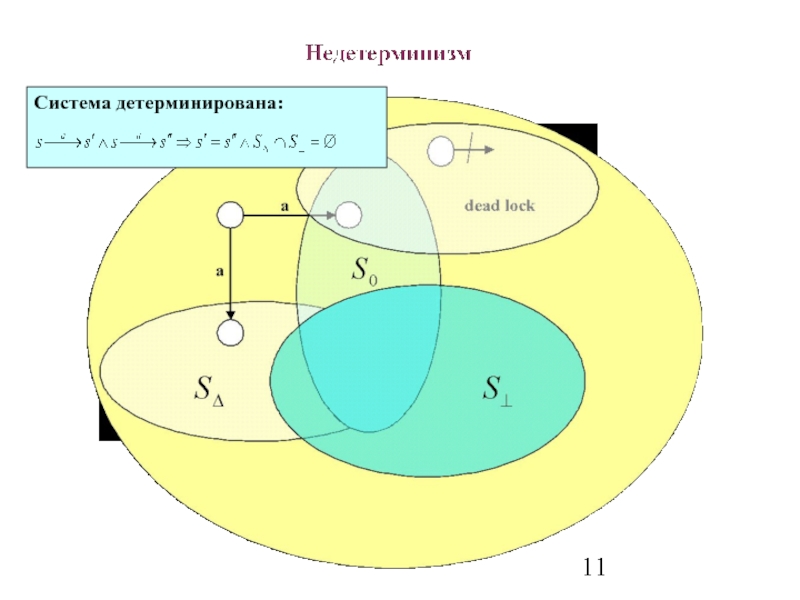
- 11. Система детерминирована:
- 12. s s'
- 13. Бисимуляционная эквивалентность bisimilarity (Milner 1980, D.Park 1981) Отношение бисимуляции (bisimulation):
- 14. Бисимуляция есть эквивалентность Бисимуляционная эквивалентность состояний совпадает с максимальной бисимуляцией на S.
- 15. Отношение бисимуляции распространяется на состояния разных
- 16. Бисимуляционная эквивалентность смешанных систем
- 17. Редукция смешанных систем Добавляем новые
- 18. Смешанная транзиционная система и ее редукция бисимуляционно эквивалентны бисимуляция смешанная система ее редукция
Слайд 2План лекций
Теория взаимодействующих процессов (CCS, CSP, ACP)
Инсерционное программирование (агенты и
Темпоральная логика и проверка моделей (model checking)
Верификация софтвера (MSC, SDL, UML)
Пруверы и солверы
Слайд 3Теории взаимодействия и параллелизма (communication, interaction and concurrency)
Структурная теория автоматов
Сети Петри
CCS
CSP (T.Hoar)
ACP (J.A.Bergstra, J.W.Klop) => Handbook on Process Algebra (2000)
Коалгебры (J.J.M.M.Rutten, TCS 249(2000))
Mobile ambients (L.Cardelli, A.Gordon)
Агенты и среды (инсерционное программирование)
(A.Letichevsky, D.Gilbert, 1999)
Слайд 4Транзиционные системы
Ординарные транзиционные (динамические) системы :
S – пространство состояний
Т – отношение
Транзитивное замыкание
Движение в фазовом пространстве (поток)
Изменение состояния электронной системы
Изменение состояния софтверной системы
Слайд 5D.Park (1981)
Размеченные транзиционные системы
А – множество меток
символы,
действия
Автоматы:
входные символы, вход/выход
Программы:
операторы, условия
Исчисления:
состояния – формулы,
действия – правила вывода
Взаимодействующие распределенные системы:
передача (прием) сообщений
Базы данных
запросы, ответы
Слайд 7Атрибутные транзиционные системы
D={0,1}
(Не размеченные переходы)
Автоматы Мура
Программы над памятью
Типизированная память
Системы Крипке (модальная
Слайд 8Настроенные системы
Другие важные классы транзиционных систем:
Стохастические и нечеткие;
Системы реального времени.
заключительные состояния
неопределенные состояния
Слайд 9
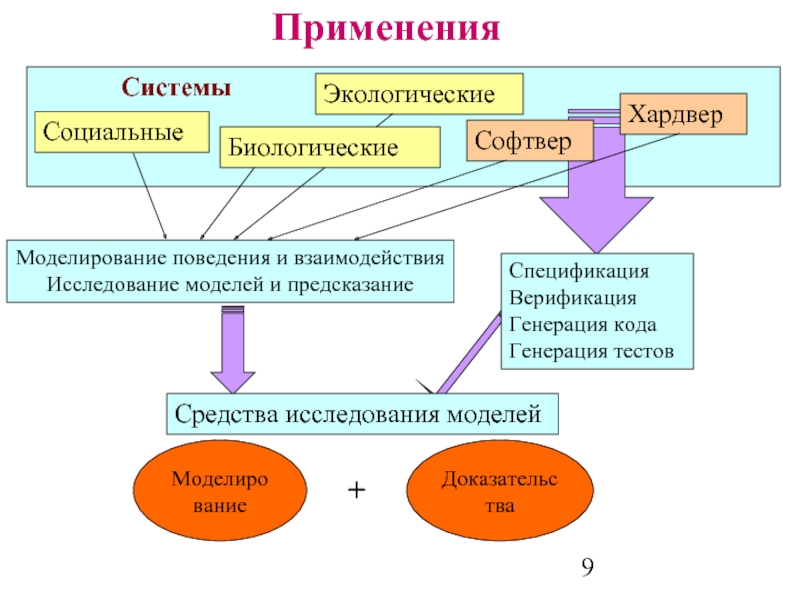
Применения
Моделирование поведения и взаимодействия
Исследование моделей и предсказание
Спецификация
Верификация
Генерация кода
Генерация тестов
Софтвер
Хардвер
Экологические
Социальные
Средства исследования моделей
Доказательства
Моделирование
+
Системы
Биологические
Слайд 13Бисимуляционная эквивалентность
bisimilarity (Milner 1980, D.Park 1981)
Отношение бисимуляции (bisimulation):
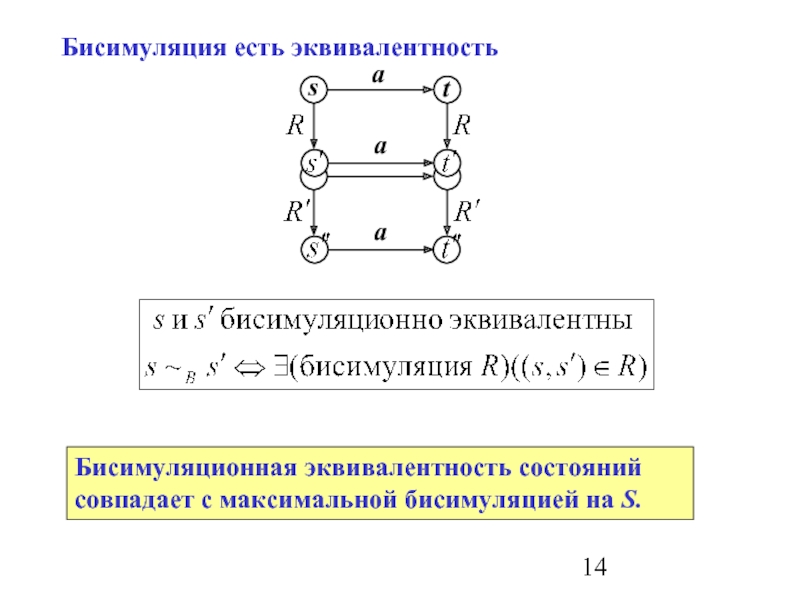
Слайд 14Бисимуляция есть эквивалентность
Бисимуляционная эквивалентность состояний совпадает с максимальной бисимуляцией на S.
Слайд 15Отношение бисимуляции распространяется на
состояния разных систем.
Для детерминированных систем бисимуляционная
эквивалентность состояний совпадает с трассовой.
Бисимуляционная эквивалентность систем
Слайд 17Редукция смешанных систем
Добавляем новые переходы и настройку состояний:
Удаляем скрытые переходы