- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сочетания презентация
Содержание
- 1. Сочетания
- 2. План урока: Рассмотрение случая выборок двух элементов.
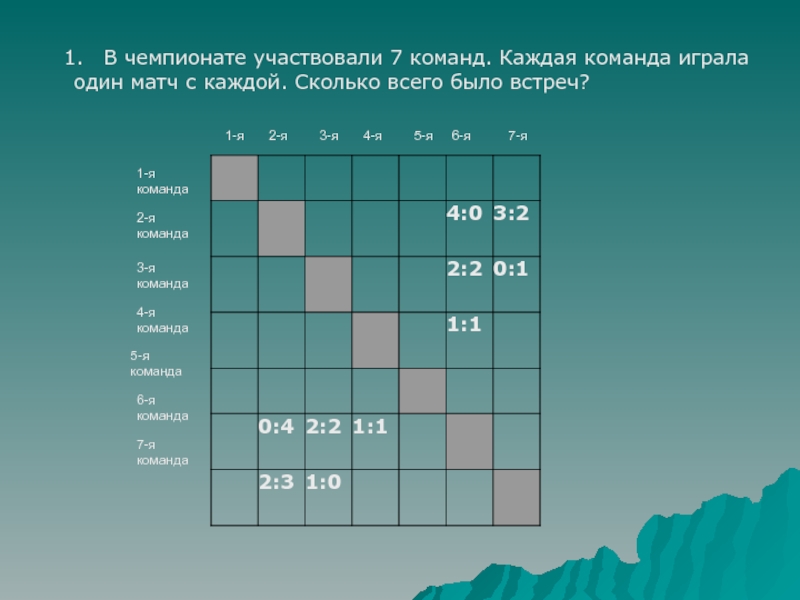
- 3. 1-я команда 3-я команда 5-я
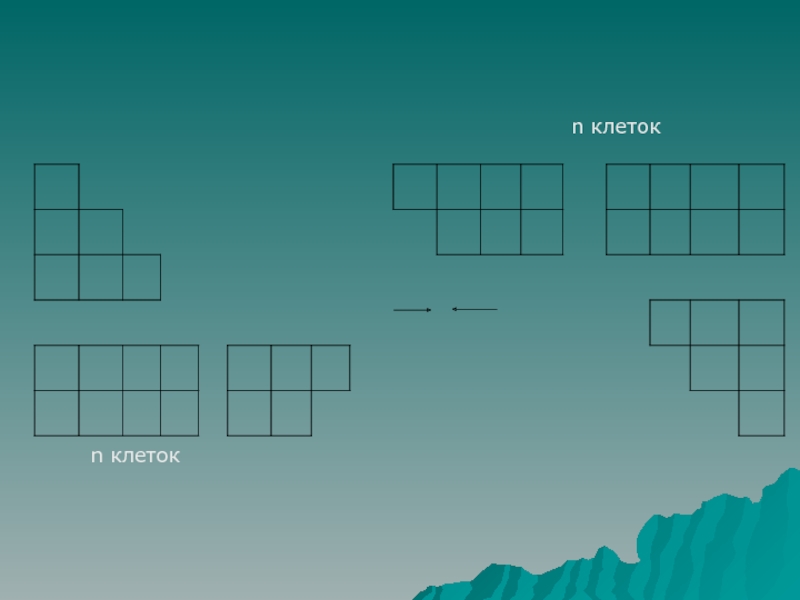
- 4. n клеток n клеток
- 5. n n+1
- 6. Теорема 1. (о выборках двух элементов). Если
- 7. Порядок важен Порядок не важен
- 8. 2. В классе 25 учеников, из
- 9. Теорема 2. (о выборках трех элементов).
- 10. Порядок важен Порядок не важен
- 11. Теорема 3. Для числа сочетания из
- 12. 3. «Проказница Мартышка, Осел, Козел и косолапый
- 13. 4. Встретились 11 футболистов и 6 хоккеистов
- 14. 5. В классе 27 учеников. К доске
Слайд 2План урока:
Рассмотрение случая выборок двух элементов.
Рассмотрение случая выборок трех элементов.
Рассмотрение
Решение задач на нахождение числа сочетаний.
Слайд 31-я
команда
3-я
команда
5-я
команда
4-я
команда
2-я
команда
6-я
команда
7-я
команда
1-я
2-я
3-я
4-я
5-я
6-я
7-я
В чемпионате участвовали 7
один матч с каждой. Сколько всего было встреч?
Слайд 6Теорема 1. (о выборках двух элементов). Если
множество состоит из n
то у него имеется
подмножеств, состоящих из двух элементов.
Слайд 8 2. В классе 25 учеников, из которых нужно выбрать
если: а) первый ученик должен решить уравнение,
второй — сходить за мелом, третий — пойти
дежурить в столовую; б) им следует спеть хором?
Слайд 9Теорема 2. (о выборках трех элементов).
Если множество состоит из n
элементов, то у него имеется
подмножеств, состоящих из
трех элементов
Слайд 123. «Проказница Мартышка, Осел, Козел и косолапый
Мишка затеяли сыграть квартет».
принести со склада 9 каких-нибудь попавшихся под
лапы музыкальных инструментов из имеющихся
14 инструментов. Сколько способов выбора есть у
Мишки?
Слайд 134. Встретились 11 футболистов и 6 хоккеистов и каждый
стал по
а) Сколько встреч было между футболистами?
б) Сколько встреч было между хоккеистами?
в) Сколько встреч было между футболистами и
хоккеистами?
Слайд 145. В классе 27 учеников. К доске нужно вызвать двоих.
Сколькими
а) первый ученик должен решить задачу по алгебре,
а второй – по геометрии;
б) они должны быстро стереть с доски?
Решение: Для стирания с доски порядок вызова учеников не важен, а в первом случае существен. Тут применимо правило умножения. Учитель сначала вызывает решать алгебраическую задачу одного из 27 учеников, а затем независимым образом вызывает одного из оставшихся 26 учеников решать задачу по геометрии. Получается 27 • 26 = 702 способа вызова.
Если во втором случае начать считать, как и в первом, то любую пару учеников мы посчитаем дважды. Например, сначала Коля, потом Катя, или сначала Катя, потом Коля. Значит, количество вызовов без учета порядка будет ровно в два раза меньше, чем количество вызовов с учетом порядка. Ответ: а) 702; б) 351.