- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления и двоичное представление информации в памяти компьютера презентация
Содержание
- 1. Системы счисления и двоичное представление информации в памяти компьютера
- 2. Десятичная система счисления Обзор десятичной системы счисления
- 3. Система счисления – это способ записи чисел
- 4. Алфавит: 0, 1, 2, 3, 4, 5,
- 5. Все мы пользуемся десятичной системой счисления в
- 6. Двоичная система счисления Характеристика системы. Перевод чисел из двоичной системы счисления в десятичную и обратно.
- 7. Алфавит: 0, 1 Основание (количество цифр): 2
- 8. Перевод 2 → 10
- 9. Дано число: 11101012 Задача: перевести число
- 10. Обобщенный метод: 1. Деление числа в
- 11. Дано число: 1172 Задача: перевести число
- 12. 128 → X2 = Примеры
- 13. Предположим у нас есть число «пять».
- 14. 00110010 ? Сколько значащих нулей
Слайд 1Системы счисления и двоичное представление информации в памяти компьютера
Десятичная и двоичная
Слайд 3Система счисления – это способ записи чисел с помощью специальных знаков
Числа: 123, 45678, 1010011, CXL
Цифры: 0, 1, 2, … I, V, X, L, …
Алфавит – это набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Типы систем счисления:
непозиционные – значение цифры не зависит от ее места (позиции) в записи числа;
позиционные – значение цифры зависит от ее места (позиции) в записи числа;
Общие термины
Слайд 4Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание
Позиционная система: значение цифры определяется ее позицией в записи числа.
Характеристика десятичной системы счисления
4 1 2 9 =
0
1
2
3
= 4x103 +1x102 +2x101 +9x100
тысячи
сотни
десятки
единицы
Слайд 5Все мы пользуемся десятичной системой счисления в которой числа соответствуют следующим
Цифры в десятичной системе
Видно, что после числа «девять» в десятичной системе нет соответствующих знаков для обозначения чисел.
Для этого используется сочетание нескольких знаков (например, для «десяти» это «1» и «0»).
Слайд 6Двоичная система счисления
Характеристика системы. Перевод чисел из двоичной системы счисления в
Слайд 7Алфавит: 0, 1
Основание (количество цифр): 2
Позиционная система: значение цифры определяется ее
Характеристика двоичной системы счисления
1 1 0 12 =
0
1
2
3
= 1x23 + 1x22 + 0x21 + 1x20 =
= 8 + 4 + 0 + 1 = 1310
Слайд 9Дано число: 11101012
Задача: перевести число в десятичную систему.
Вычисление:
1110101=
Пример на перевод
0
1
2
3
4
5
6
=1*26+1*25+1*24+0*23+1*22+0*21+1*20 =
= 64 + 32 + 16 + 0 + 4 + 0 + 1 = 117
Слайд 10Обобщенный метод:
1. Деление числа в 10-ой системе на основание двоичной системы
2. Деление полученного частного на 2.
3. Повторять шаги 1-2 пока частное не будет меньше основания системы (меньше 2).
4. Записать последнее частное и все остатки от деления в обратном порядке.
Перевод 10 → 2
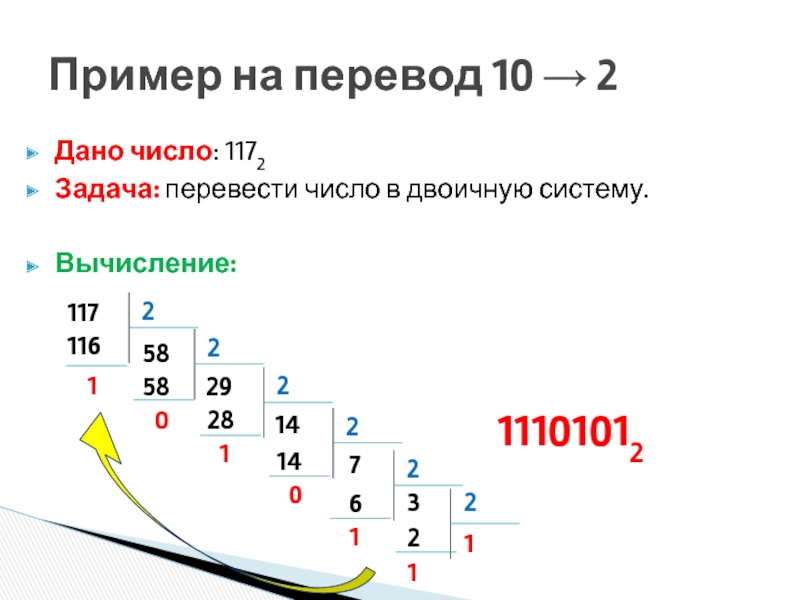
Слайд 11Дано число: 1172
Задача: перевести число в двоичную систему.
Вычисление:
Пример на перевод
117
2
116
1
58
2
58
29
0
2
28
1
14
2
14
0
7
2
6
1
3
2
2
1
1
11101012
Слайд 12128 → X2 =
Примеры для самостоятельного решения
10000000
1001111
93
102
79 → Y2 =
1011101
1100110 → B10 =
Слайд 13Предположим у нас есть число «пять».
В случае записи нуля(-ей) слева
005 = 05 = 5
В этом случае нули незначащие (т.к. не влияют на значение числа)
В случае записи нуля(-ей) справа от цифры 5, мы получаем другие числа, отличные от пяти:
500 = 50 = 5
В этом случае нули значащие (т.к. влияют на значение числа)
Значащие нули