оттуда
Таскают двое дураков.
Сия работа им приятна,
Они таскают t минут,
И, вынув шар, его обратно
Тотчас немедленно кладут.
Ввиду занятия такого,
Сколь вероятность велика,
Что первый был глупей второго,
Когда шаров он вынул k?
В. П. Скитович
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Схема Бернулли презентация
Содержание
- 1. Схема Бернулли
- 2. Введение Испытание, в результате которого ожидается наступление
- 3. Якоб Бернулли 27 декабря 1654, Базель, — 16
- 4. Схема Бернулли Рассматривают n независимых повторений одного
- 5. Примечание При n независимых повторений одного и
- 6. Теорема Бернулли Вероятность Pn(k) наступления ровно k
- 7. Пример использования теоремы Бернулли Каждый из 4
- 8. Решение: Если кому-то достался известный ему вопрос,
- 9. Доказательство теоремы Бернулли на примере Найти вероятность
- 10. Решение В данном примере формула Бернулли доказывается,
- 11. Продолжение решения Обозначим A279 событие, состоящее в
- 12. Распределение числа «успехов» Таблица распределения вероятностей числа
- 13. Биномиальное распределение Если сложить все числа второй
- 14. Пример использования таблицы распределения Вероятность того, что
- 15. Решение По условию, n=5; p=0,4; q=0,6; k=0,1,2,3,4,5:
- 16. Продолжение решения «Ни разу не промахнется» -
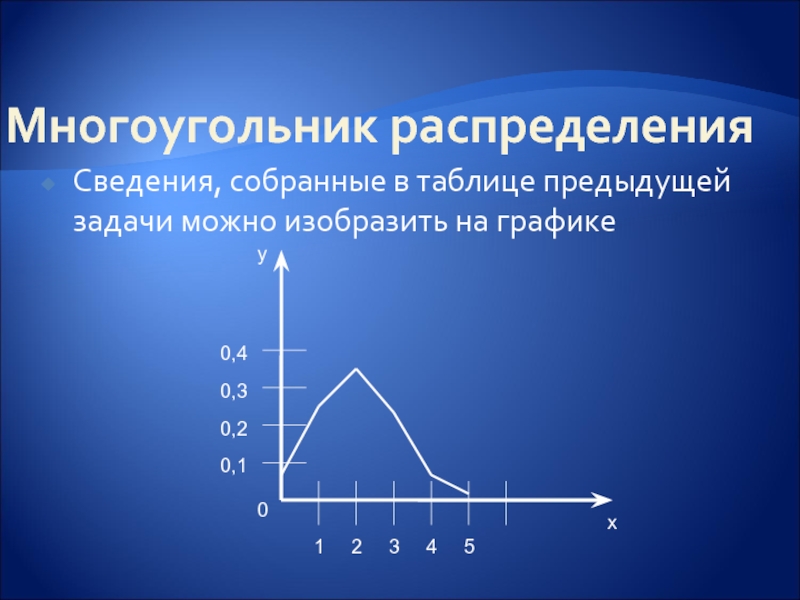
- 17. Многоугольник распределения Сведения, собранные в таблице предыдущей
- 18. Ломаную, соединяющую отмеченные на графике точки, называют многоугольником распределения.
- 19. Важное замечание Последовательность чисел Pn(0), Pn(1), Pn(2),…,
- 20. Использование данного замечания Найти наивероятнейшее число выпадений
- 21. Решение а) В данном случае n=100, p=q=0,5.
- 22. Теорема Наиболее вероятное число «успехов» в n
- 23. И напоследок одно правило… Для того, чтобы
- 24. Презентацию подготовил Кузнецов Игорь ученик 11 Б класса МОУ «Гимназия №11»
- 25. СПАСИБО ЗА ВНИМАНИЕ! Успехов в изучении теории вероятностей!
Слайд 2Введение
Испытание, в результате которого ожидается наступление интересующего нас события, можно многократно
повторять. Главный вопрос каждого повторения – произойдет или не произойдет это событие? А во всей серии повторений важно знать, сколько именно раз оно может произойти или не произойти. Например, какова вероятность, что при пяти бросаниях монеты «орел» выпадет ровно 4 раза? Швейцарский математик начала XVIII века Якоб Бернулли объединил подобные вопросы в единую вероятностную схему, которую принято называть схемой Бернулли.
Слайд 3Якоб Бернулли
27 декабря 1654, Базель, — 16 августа 1705, там же — швейцарский
математик, старший брат Иоганна Бернулли; профессор математики Базельского университета (с 1687 года).
Слайд 4Схема Бернулли
Рассматривают n независимых повторений одного и того же испытания с
двумя возможными исходами: «успехом» и «неудачей». Вероятность «успеха» равна p, а вероятность неудачи равна q. Известна формула – p+q=1. Требуется найти вероятность Pn(k) того, что в этих повторениях произойдет ровно k «успехов».
Слайд 5Примечание
При n независимых повторений одного и того же испытания с двумя
возможными исходами более кратко говорят как об n испытаниях Бернулли
Слайд 6Теорема Бернулли
Вероятность Pn(k) наступления ровно k «успехов» в n независимых повторениях
одного и того же испытания вычисляется по формуле
Pn (k)=Ckpkqn-k,
где p – вероятность «успеха», а q=1-p – вероятность неудачи в отдельном испытании.
Pn (k)=Ckpkqn-k,
где p – вероятность «успеха», а q=1-p – вероятность неудачи в отдельном испытании.
n
Слайд 7Пример использования теоремы Бернулли
Каждый из 4 приятелей выучил ровно 5 вопросов
из 20 заданных к зачету. На зачете они отвечали в разных аудиториях и получали вопросы независимо друг от друга. Найти вероятность того, что:
а) каждому достался тот вопрос, который он выучил;
б) никому не достался вопрос, который он выучил;
в) только одному достался вопрос, который он не выучил;
г) хотя бы одному достался вопрос, который он выучил.
а) каждому достался тот вопрос, который он выучил;
б) никому не достался вопрос, который он выучил;
в) только одному достался вопрос, который он не выучил;
г) хотя бы одному достался вопрос, который он выучил.
Слайд 8Решение:
Если кому-то достался известный ему вопрос, то это «успех». Вероятность «успеха»
у каждого из приятелей одинакова: она равна 5/20=0,25. Поэтому можно считать, что мы имеем дело с n = 4 испытаниями Бернулли с вероятностью «успеха» в отдельном испытании p=0,25.
а) В этом случае k=n=4 и поэтому P4(4)=C4p4q4-4=0,254≈0,004.
б) В этом случае k=0 и поэтому P4(0)=C0p0q4-0=0,754 ≈0,316.
в) Здесь k=3 и поэтому P4(3)=C3p3q4-3=4*0,253*0,75 ≈0,047.
г) Событие, противоположное заданному, состоит в том, что никому из приятелей не достался известный ему вопрос, т.е. что произошло k=0 «успехов». Вероятность такой общей неудачи уже посчитана в пункте б). Значит, нужная нам вероятность равна 1-P4(0)=1-0,754 ≈0,684
а) В этом случае k=n=4 и поэтому P4(4)=C4p4q4-4=0,254≈0,004.
б) В этом случае k=0 и поэтому P4(0)=C0p0q4-0=0,754 ≈0,316.
в) Здесь k=3 и поэтому P4(3)=C3p3q4-3=4*0,253*0,75 ≈0,047.
г) Событие, противоположное заданному, состоит в том, что никому из приятелей не достался известный ему вопрос, т.е. что произошло k=0 «успехов». Вероятность такой общей неудачи уже посчитана в пункте б). Значит, нужная нам вероятность равна 1-P4(0)=1-0,754 ≈0,684
4
4
4
Слайд 9Доказательство теоремы Бернулли на примере
Найти вероятность того, что при десяти бросаниях
игрального кубика «четверка» выпадет ровно три раза
Слайд 10Решение
В данном примере формула Бернулли доказывается, а не применяется для вычислений.
В данном примере n=10, k=3, а «успех» состоит в выпадении «четверки» при одном бросании, поэтому p=1/6, q=5/6. Обозначим А123 событие, состоящее в том, что «четверка» выпадет только при первом, втором и третьем бросаниях. Вероятность этого события: P(A123)=N(A123)/N. По правилу умножения при 10 независимых бросаниях кубика имеется N=610 равновозможных исходов. Найдем N(A123), т.е. количество тех исходов, в которых наступает событие A123. Для первых трех бросаний имеется по одному возможному исходу, а для всех остальных бросаний имеется ровно по 5 исходов: может выпасть 1, 2, 3, 5 или 6. По правилу умножения получаем, что N(A123)=1*1*1*5*5*…*5=57. Значит, P(A123)=N(A123)/N=57/610=(13*57)/(63*67)=(1/6)3*(5/6)7=p3q7.
Слайд 11Продолжение решения
Обозначим A279 событие, состоящее в том, что»четверка» выпала только при
втором, седьмом и девятом бросаниях кубика. Вероятность P(A279) находится точно так же, как и вероятность P(A123). Такой же ответ получается и для событий A134, A458, A567, …, и для любого события Axyz, состоящего в том, что «четверка» выпала именно при бросаниях с номерами x, y, z. Все события Axyz между собой попарно несовместны. Вероятность P(Axyz) каждого из событий Axyz равна p3q7. Количество этих событий равно количеству выборов трех номеров из 10 данных без учета порядка, т.е. равно С3. По теореме суммы для нахождения вероятности несовместных событий получаем:
P(A)=p3q7 + p3q7 + … + p3q7=C3p3q7.
C3 раз
P(A)=p3q7 + p3q7 + … + p3q7=C3p3q7.
C3 раз
10
10
10
Слайд 12Распределение числа «успехов»
Таблица распределения вероятностей числа «успехов» в n испытаниях Бернулли.
… …
n
n
Слайд 13Биномиальное распределение
Если сложить все числа второй строки предыдущей таблицы, то получится
1:
1=C0qn+C1pqn-1+…+Ckpkqn-k+…+Cn-1pn-1q+Cnpn.
Можно отметить, что данное равенство есть частный случай формулы бинома Ньютона:
(q+p)n= C0qn+C1pqn-1+…+Ckpkqn-k+…+Cn-1pn-1q+Cnpn
По этой причине распределение числа «успехов» в испытаниях Бернулли по вероятности их наступления, как правило, называют биномиальным распределением.
1=C0qn+C1pqn-1+…+Ckpkqn-k+…+Cn-1pn-1q+Cnpn.
Можно отметить, что данное равенство есть частный случай формулы бинома Ньютона:
(q+p)n= C0qn+C1pqn-1+…+Ckpkqn-k+…+Cn-1pn-1q+Cnpn
По этой причине распределение числа «успехов» в испытаниях Бернулли по вероятности их наступления, как правило, называют биномиальным распределением.
n
n
n
n
n
n
n
n
n
n
Слайд 14Пример использования таблицы распределения
Вероятность того, что стрелок поразит мишень при одном
выстреле, равна 0,4. Стрелок производит независимо 5 выстрелов. Составить таблицу распределения вероятностей числа попаданий. Найти вероятность того, что стрелок ни разу не промахнется.
Слайд 15Решение
По условию, n=5; p=0,4; q=0,6; k=0,1,2,3,4,5:
P5(0)=C0p0q5=0,65≈0,078;
P5(1)=C1pq4=5*0,4*0,64 ≈0,259;
P5(2)=C2p2q3=10*0,42*0,63 ≈0,346;
P5(3)=C3p3q2=10*0,43*0,62 ≈0,23;
P5(4)=C1p4q=5*0,44*0,6 ≈0,077;
P5(5)=C5p5q0=0,45≈0,01.
5
5
5
5
5
5
Слайд 16Продолжение решения
«Ни разу не промахнется» - это значит, что стрелок поразит
мишень все 5 раз, т.е. k=5. Из таблицы следует, что Вероятность примерно равна 0,01.
Слайд 17Многоугольник распределения
Сведения, собранные в таблице предыдущей задачи можно изобразить на графике
x
y
0
1
2
3
4
5
0,1
0,2
0,3
0,4
Слайд 19Важное замечание
Последовательность чисел Pn(0), Pn(1), Pn(2),…, Pn(k),…, Pn(n-1), Pn(n) сначала возрастает,
а затем, приняв наибольшее значение, убывает. Только в некоторых специальных случаях наибольшее значение достигается не для одного, а для двух соседних значений k. Можно доказать, что вероятность Pn(k) принимает наибольшее значение при значении k, равном ближайшему к np-q справа целому числу. Если же само число np-q целое, то наибольшее значение вероятность принимает для двух значений k: для k=np-q и для k=np+p.
Слайд 20Использование данного замечания
Найти наивероятнейшее число выпадений решки при: а) 100 бросаниях
монеты; б) 1001 бросании монеты.
Слайд 21Решение
а) В данном случае n=100, p=q=0,5. Тогда число np-q=100*0,5-0,5=49,5 – не
целое. Ближайшее к нему справа целое число равно 50. Оно равно половине числа всех бросаний и является наивероятнейшим числом выпадений решки.
б) в данном случае n=1001, p=q=0,5. Тогда число np-q=1001*0,5-0<5=500 – целое. Значит, вероятность Pn(k) числа «успехов» принимает свое наибольшее значение при k=500 и при k=501.
б) в данном случае n=1001, p=q=0,5. Тогда число np-q=1001*0,5-0<5=500 – целое. Значит, вероятность Pn(k) числа «успехов» принимает свое наибольшее значение при k=500 и при k=501.
Слайд 22Теорема
Наиболее вероятное число «успехов» в n испытаниях Бернулли приближенно равно np,
где p – вероятность «успеха» в отдельном испытании.
Например, если вероятность успеха в одном испытании равна 0,1, а вы провели 143 повторения этого испытания, то наивероятнейшее число «успехов» равно 143*0,1≈14. При таком грубом подсчете ошибка возможна, но она невелика.
Например, если вероятность успеха в одном испытании равна 0,1, а вы провели 143 повторения этого испытания, то наивероятнейшее число «успехов» равно 143*0,1≈14. При таком грубом подсчете ошибка возможна, но она невелика.
Слайд 23И напоследок одно правило…
Для того, чтобы найти наивероятнейшее число kнаивер. «успехов»
в n испытаниях Бернулли с вероятностью «успеха» равной p, следует:
1) вычислить число np;
2) от числа np на координатной прямой отложить q влево и p вправо;
3) целое число, лежащее на отрезке [np-q;np+p] единичной длины, и будет равно kнаивер.; если таких целых чисел 2, то kнаивер. может равняться любому из них.
1) вычислить число np;
2) от числа np на координатной прямой отложить q влево и p вправо;
3) целое число, лежащее на отрезке [np-q;np+p] единичной длины, и будет равно kнаивер.; если таких целых чисел 2, то kнаивер. может равняться любому из них.