- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Селекция2 презентация
Содержание
- 1. Селекция2
- 2. Анализ путей. Одним из современных методов моделирования
- 3. Путевые диаграммы Райта Кружки и квадраты соединяются
- 4. Связь регрессии, дисперсии и путевых диаграмм Райта
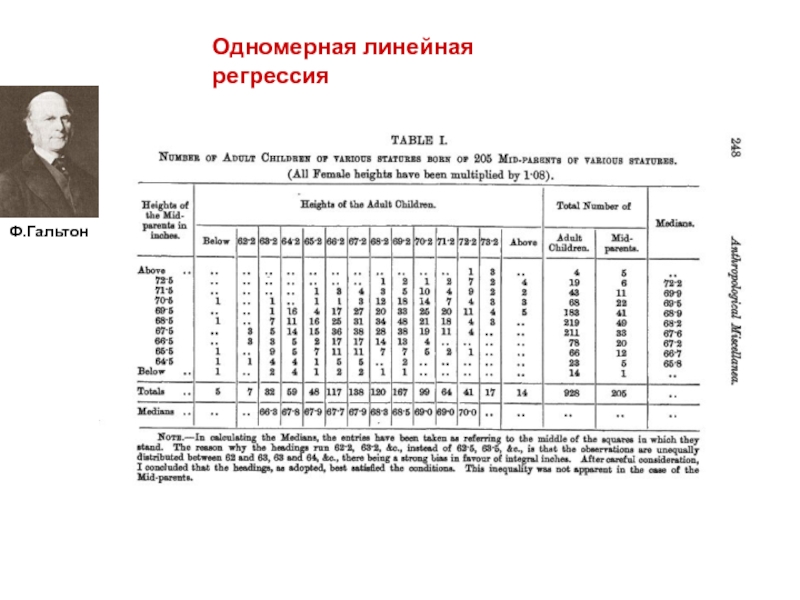
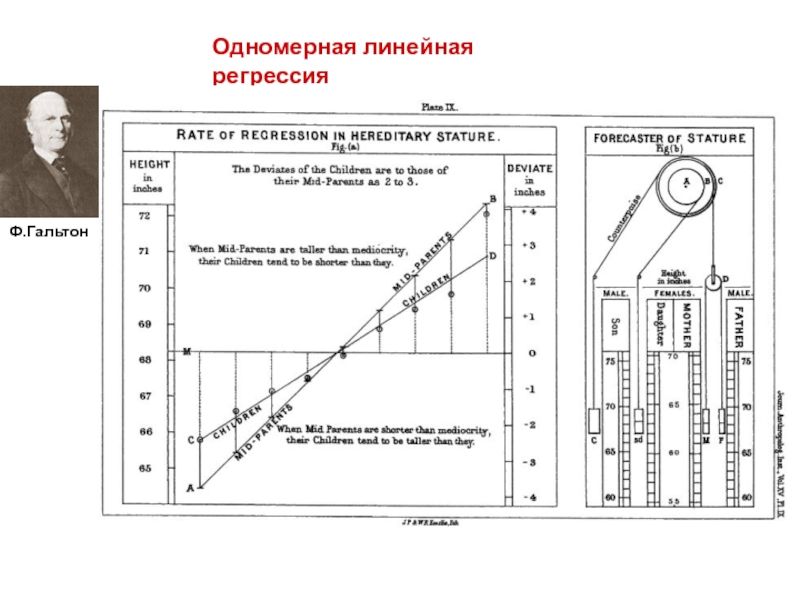
- 5. Одномерная линейная регрессия Ф.Гальтон
- 6. Одномерная линейная регрессия Ф.Гальтон
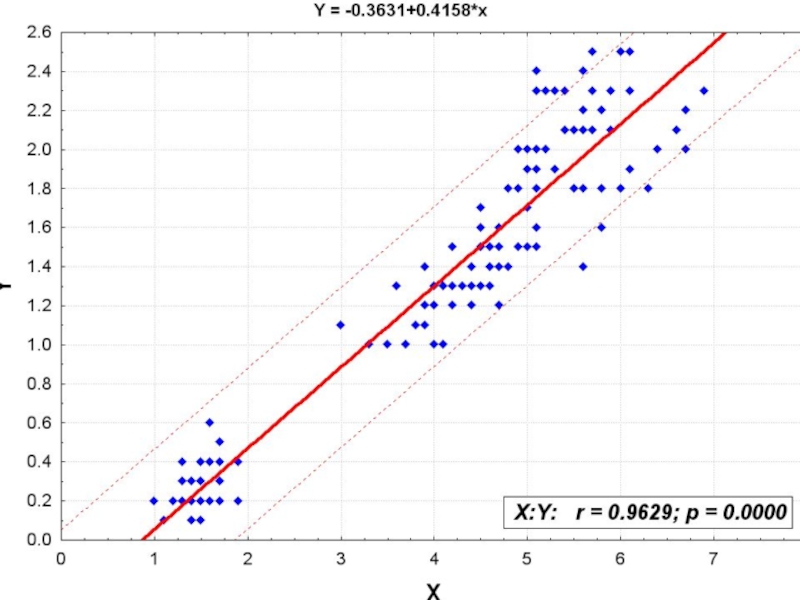
- 7. Уравнение линейной регресии. Метод наименьших квадратов
- 9. Будем считать, что обе переменные центрированы и
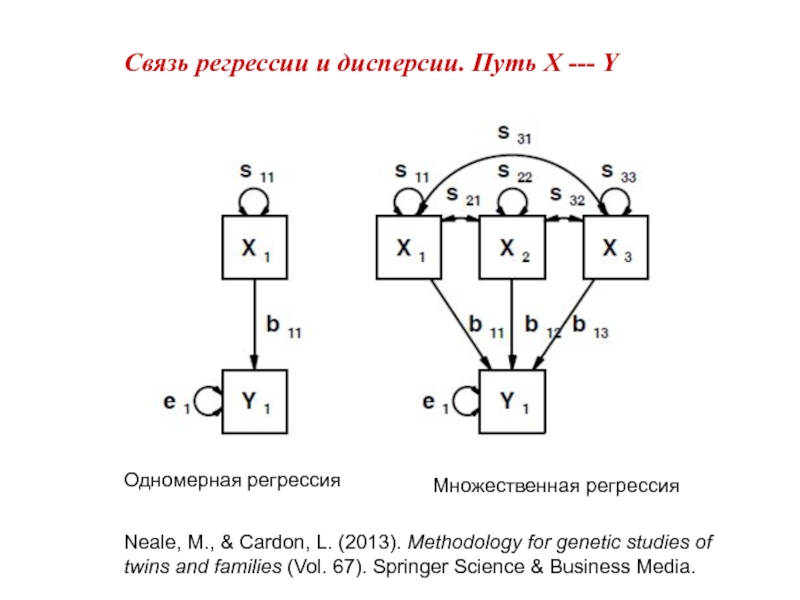
- 10. Связь регрессии и дисперсии. Путь X ---
- 11. Связь регрессии и дисперсии. Путь X ---
- 12. Связь регрессии и дисперсии. Путь X ---
- 13. Связь регрессии и дисперсии. Путь X ---
- 14. Связь регрессии и дисперсии. Путь X --- Y Главные компоненты r=0
- 15. Коэффициент наследуемости (гетерогенные
- 16. Нас интересует прежде всего аддитивный
- 17. Коэффициент наследуемости (гетерогенные
- 18. Коэффициент наследуемости (гетерогенные родители и потомки)
- 19. Коэффициент наследуемости (гетерогенные
- 20. Коэффициент наследуемости через корреляцию фенотипов мать—дочь
- 21. Коэффициент наследуемости отец-дочь через корреляцию фенотипов
- 22. Коэффициент наследуемости отец-дочь через корреляцию фенотипов
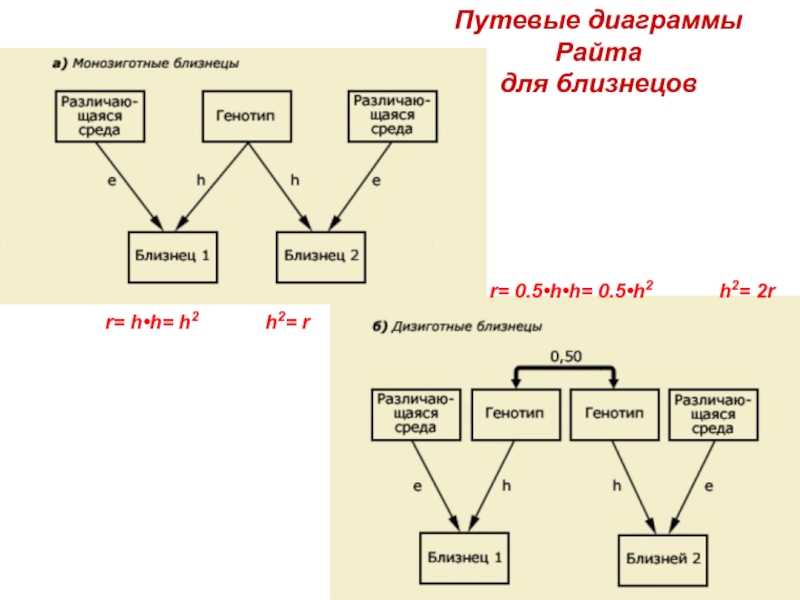
- 23. Путевые диаграммы Райта для близнецов r= 0.5•h•h=
- 24. Путевые диаграммы Райта для близнецов Диаграмма путей
- 25. Путевые диаграммы Райта для близнецов rMZ= 1•h•h+c•c=
- 26. Рх и Ру - коррелирующие фенотипические признаки;
- 27. Структурное моделирование применяется в эконометрике и представляет
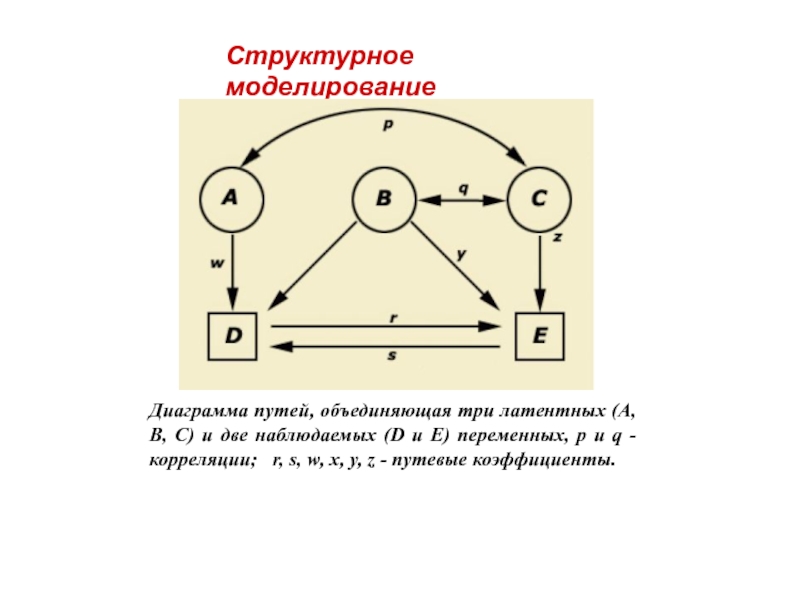
- 28. Диаграмма путей, объединяющая три латентных (А, В,
- 29. Спасибо за внимание!
- 30. H = GP-1 Многомерный аналог
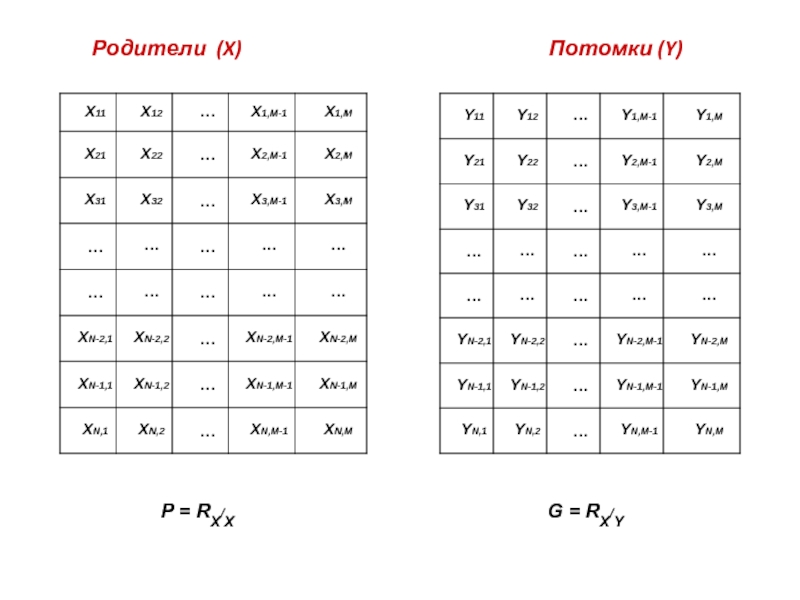
- 31. Родители (X)
- 32. Поиск осей с максимальной наследуемостью (в
- 34. Расположение центроидов родительских и гибридных выборок в
- 35. F1 - F# – ось гетерозиготности H
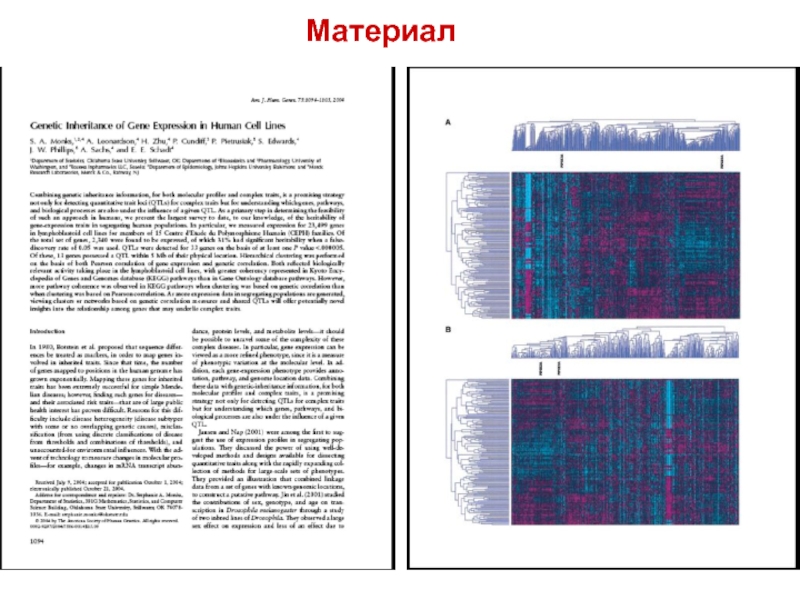
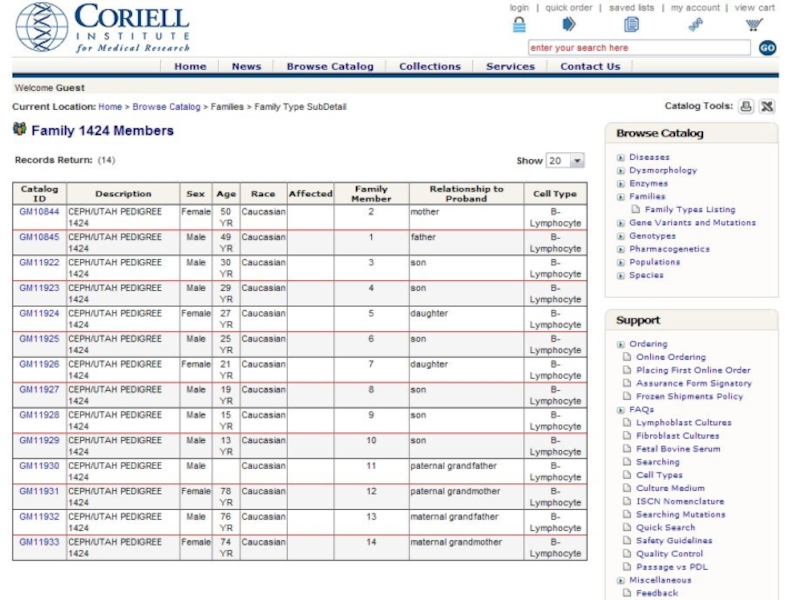
- 37. Материал
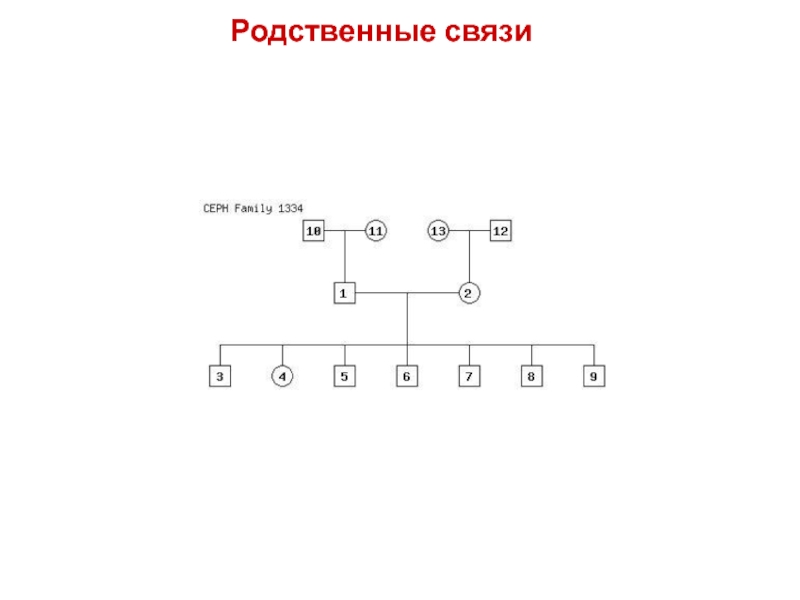
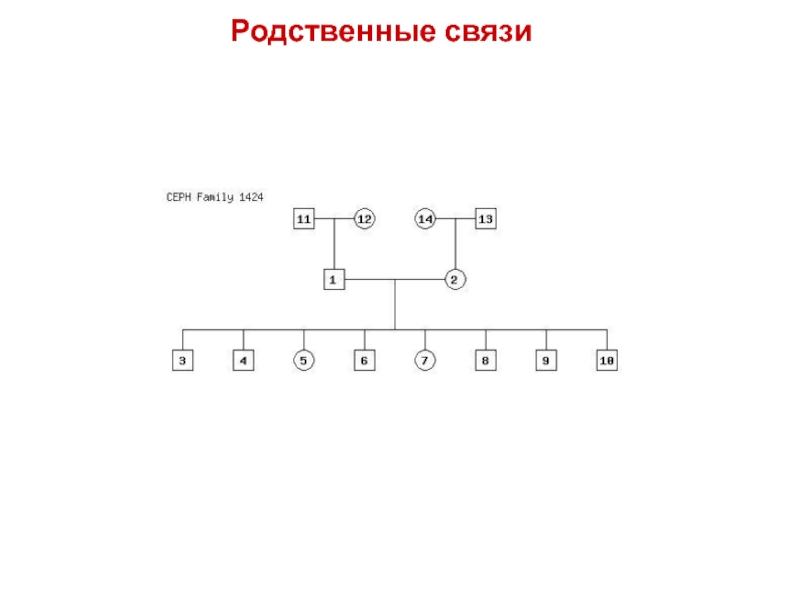
- 39. Родственные связи
- 40. Родственные связи
- 41. Коэффициенты корреляции родителей с потомками по первым
- 42. Коэффициент наследуемости
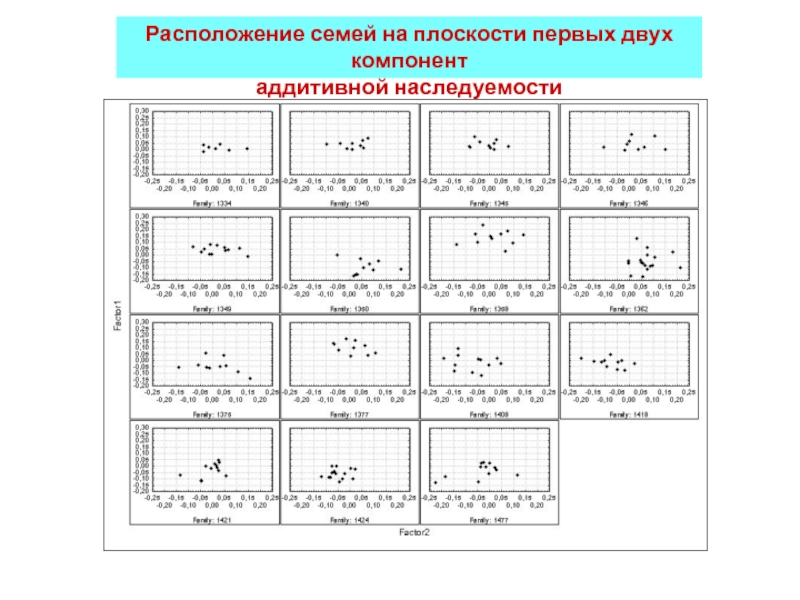
- 43. Расположение семей на плоскости первых двух компонент аддитивной наследуемости
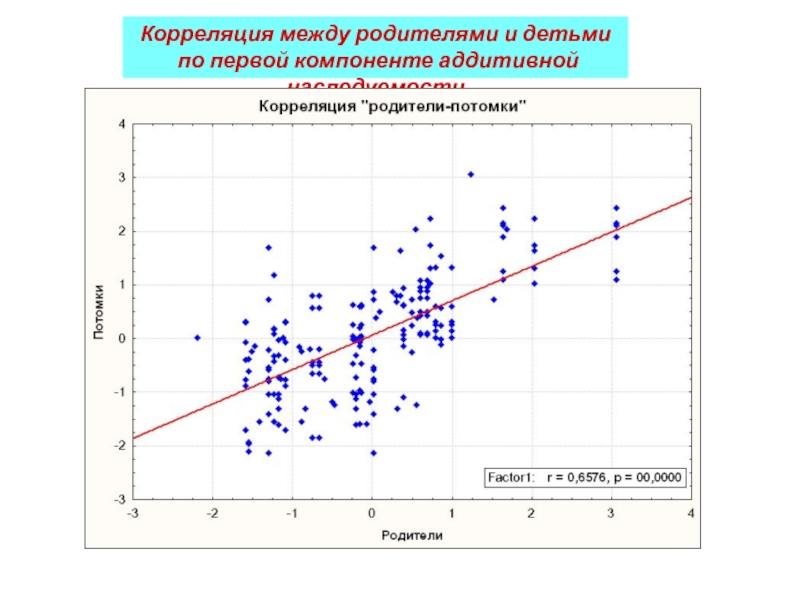
- 44. Корреляция между родителями и детьми по первой компоненте аддитивной наследуемости
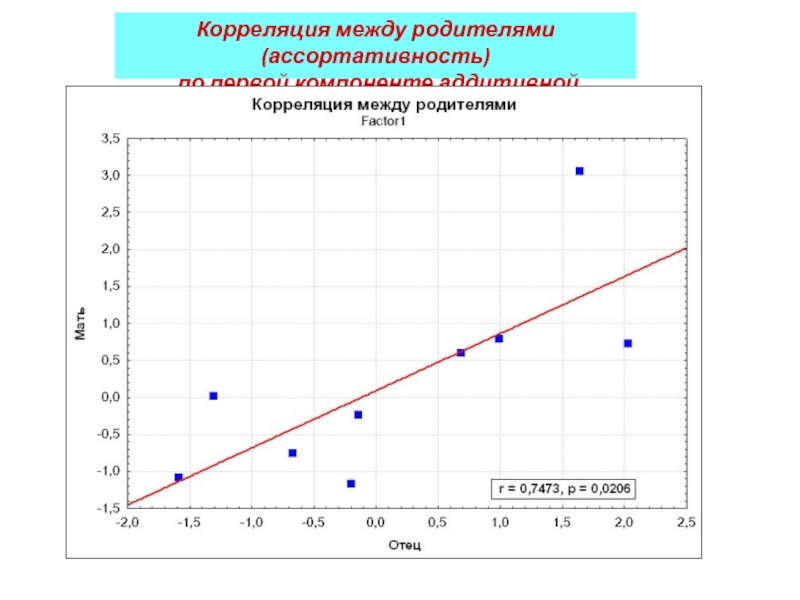
- 45. Корреляция между родителями (ассортативность) по первой компоненте аддитивной наследуемости
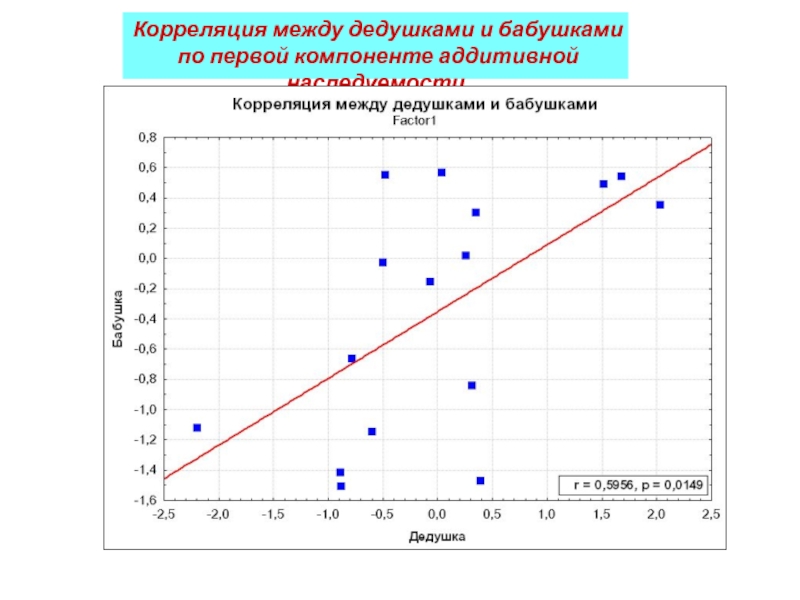
- 46. Корреляция между дедушками и бабушками по первой компоненте аддитивной наследуемости
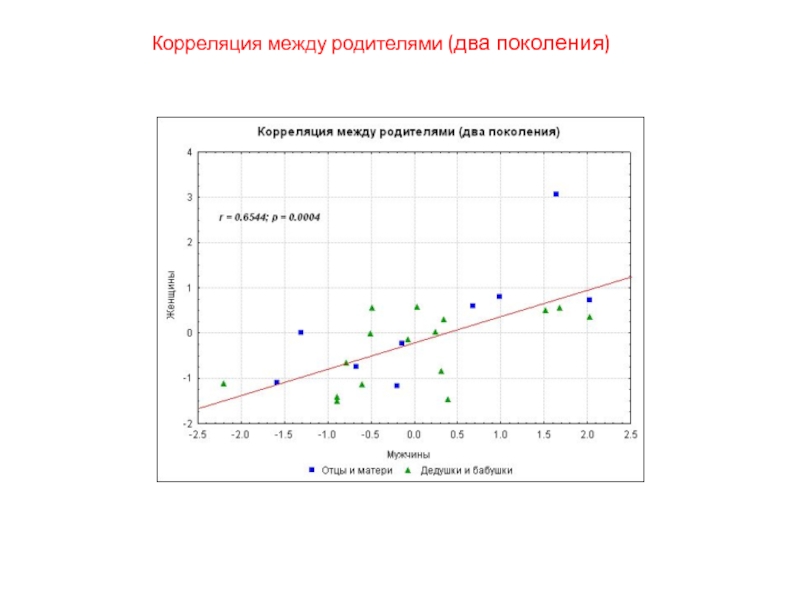
- 47. Корреляция между родителями (два поколения)
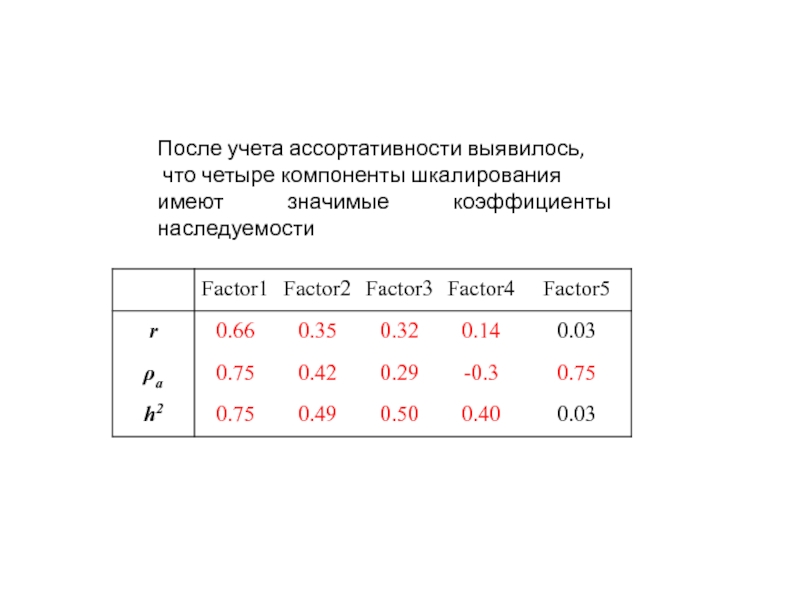
- 48. После учета ассортативности выявилось, что четыре компоненты шкалирования имеют значимые коэффициенты наследуемости
Слайд 1В.М.Ефимов, д.б.н.
Теория селекции
Лекция 2. Путевые диаграммы Райта.
Институт цитологии и генетики
Слайд 2Анализ путей. Одним из современных методов моделирования является анализ путей. Сам
Путевые диаграммы Райта
Слайд 3Путевые диаграммы Райта
Кружки и квадраты соединяются между собой стрелками, которые обозначают
Слайд 9Будем считать, что обе переменные центрированы и нормированы.
Уравнение ỹ=ax+b – это
Сколько дисперсии «снимает» такая зависимость? Сколько знания она приносит?
Слайд 10Связь регрессии и дисперсии. Путь X --- Y
∑ yi2/N= σy2= 1;
∑ yi xi /N= r;
ỹ= rx; ỹi= rxi ;
σỹ2= ∑ ỹi2/N= ∑(rxi)2/N= r2 ∑ xi2/N= r2σx2= r2
Таким образом, доля дисперсии Х в дисперсии Y равна r2.
В единицах стандартного отклонения σỹ= √(r2)= r.
Слайд 11Связь регрессии и дисперсии. Путь X --- Y
Но можно рассмотреть регрессию
Получим, что доля дисперсии Y в дисперсии X тоже равна r2.
Таким образом, ситуация симметрична.
Графически это изображается следующим образом:
X
Y
r
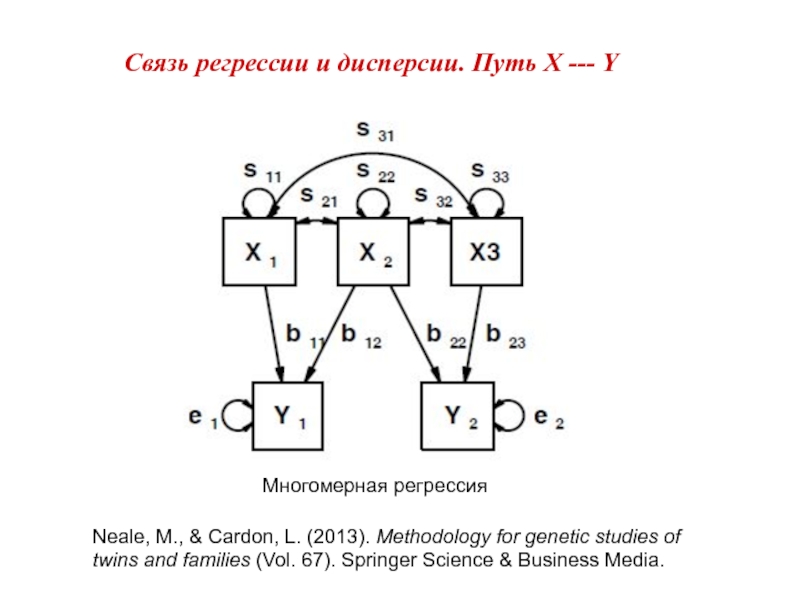
Слайд 12Связь регрессии и дисперсии. Путь X --- Y
Одномерная регрессия
Множественная регрессия
Neale, M.,
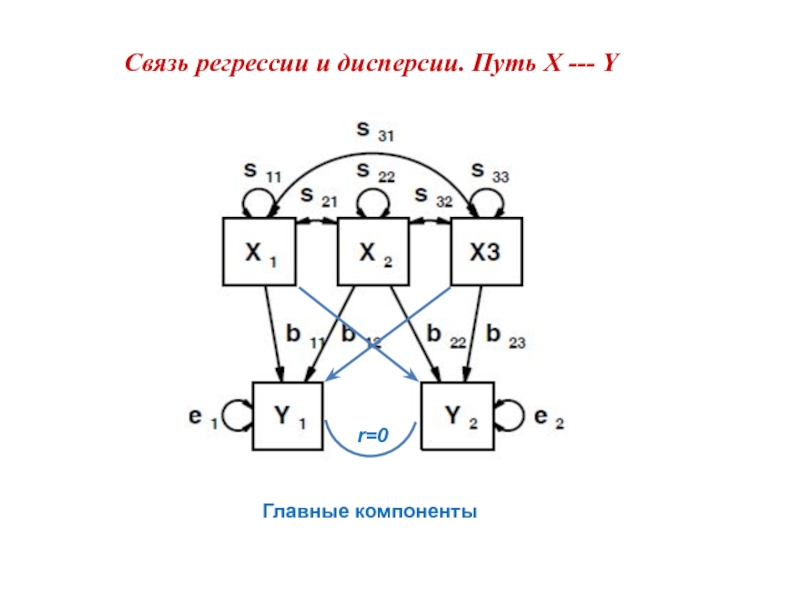
Слайд 13Связь регрессии и дисперсии. Путь X --- Y
Многомерная регрессия
Neale, M., &
Слайд 15
Коэффициент наследуемости
(гетерогенные родители и потомки)
Lush. I. L.
где σG2 – генотипическая дисперсия,
σP2 – фенотипическая дисперсия.
Слайд 16
Нас интересует прежде всего аддитивный эффект. Именно он отвечает за успешность
Коэффициент наследуемости
(гетерогенные родители и потомки)
Слайд 17
Коэффициент наследуемости
(гетерогенные родители и потомки)
в широком смысле:
в узком
То есть, коэффициент наследуемости – это доля дисперсии генотипа в дисперсии фенотипа
Слайд 18Коэффициент наследуемости
(гетерогенные родители и потомки)
G
P
h
В единицах стандартного отклонения:
Здесь ситуация
Графически это изображается следующим образом:
или : σG= hσP
Слайд 19
Коэффициент наследуемости
(гетерогенные родители и потомки)
Lush. I. L.
через корреляции “родитель-потомок”:
один родитель - потомок
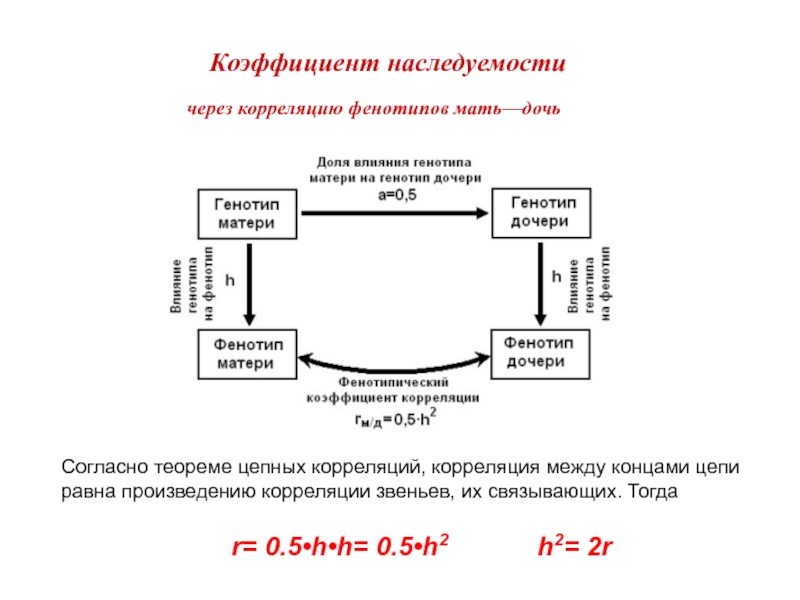
Слайд 20Коэффициент наследуемости
через корреляцию фенотипов мать—дочь
Согласно теореме цепных корреляций, корреляция между
r= 0.5•h•h= 0.5•h2 h2= 2r
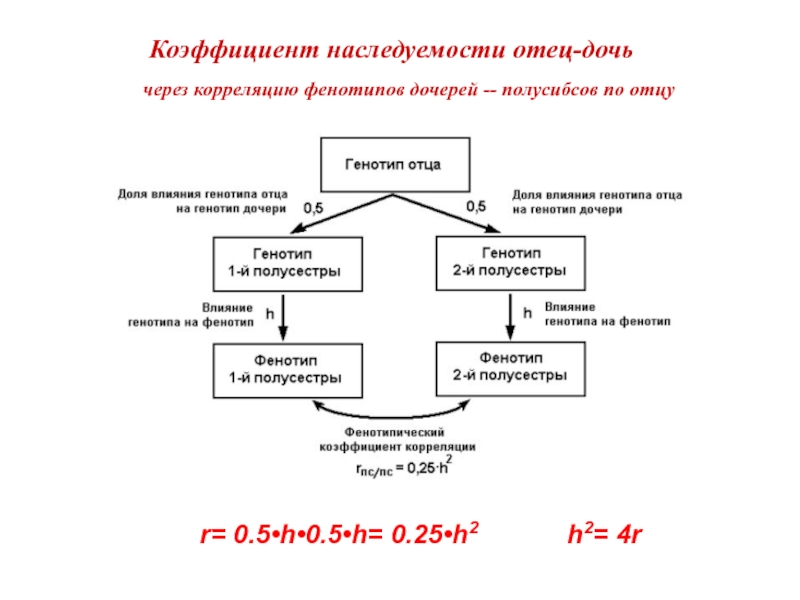
Слайд 21Коэффициент наследуемости отец-дочь
через корреляцию фенотипов дочерей -- полусибсов по отцу
Сходство
(предки — потомки), обычно оценивается коэффициентом корреляции Пирсона, который называют также межклассовым коэффициентом корреляции. В случае близнецов и сиблингов применяется коэффициент внутриклассовой корреляции, подсчитываемый на основе дисперсионного анализа:
где хi' и хi — значения одного и того же признака у членов одной пары.
Слайд 22Коэффициент наследуемости отец-дочь
через корреляцию фенотипов дочерей -- полусибсов по отцу
r=
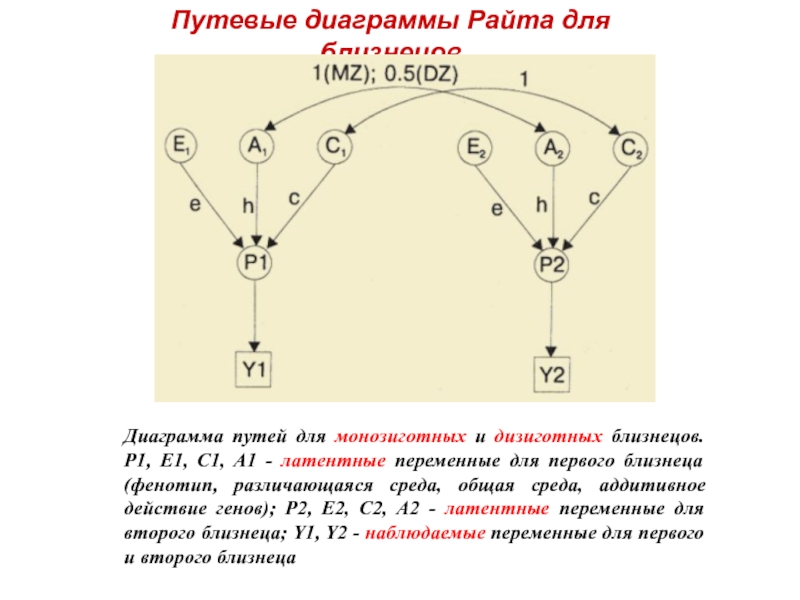
Слайд 24Путевые диаграммы Райта для близнецов
Диаграмма путей для монозиготных и дизиготных близнецов.
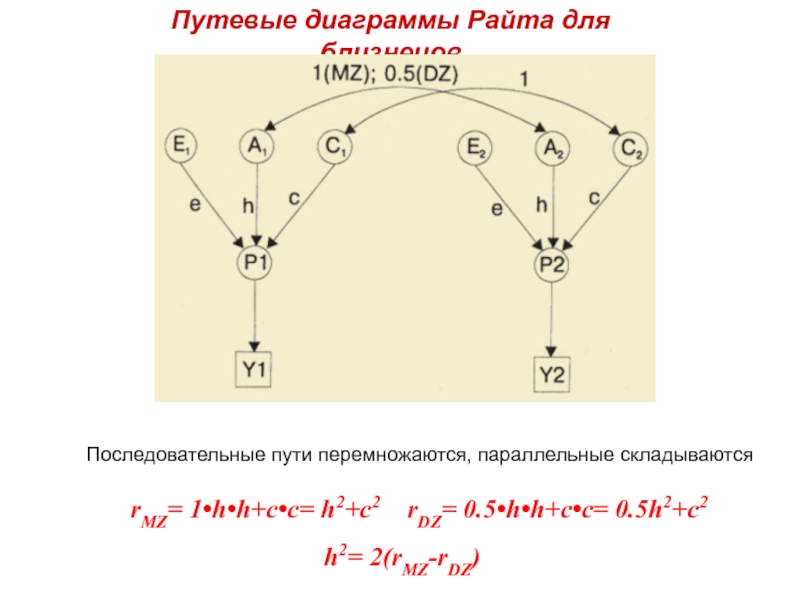
Слайд 25Путевые диаграммы Райта для близнецов
rMZ= 1•h•h+c•c= h2+c2 rDZ= 0.5•h•h+c•c=
h2= 2(rMZ-rDZ)
Последовательные пути перемножаются, параллельные складываются
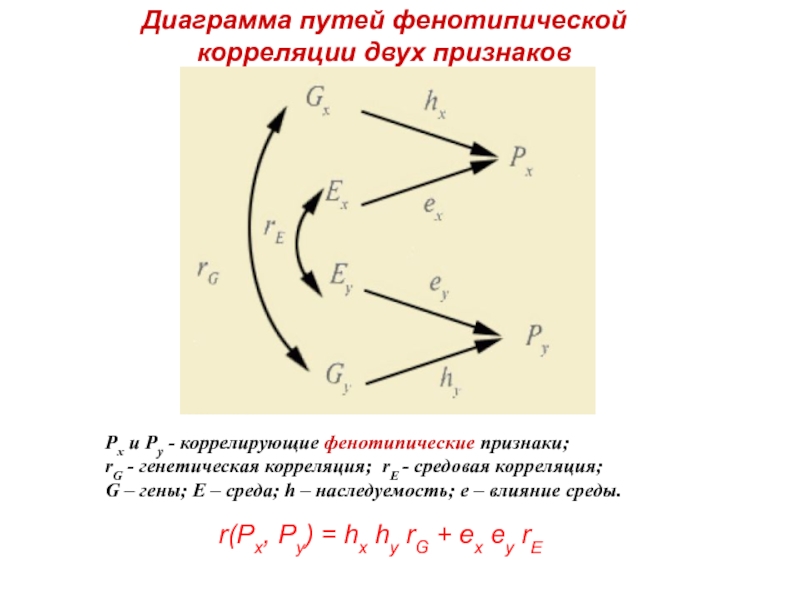
Слайд 26Рх и Ру - коррелирующие фенотипические признаки;
rG - генетическая корреляция;
G – гены; E – среда; h – наследуемость; e – влияние среды.
Диаграмма путей фенотипической корреляции двух признаков
r(Px, Py) = hx hy rG + ех еy rЕ
Слайд 27Структурное моделирование применяется в эконометрике и представляет собой один из наиболее
Структурное моделирование
Слайд 28Диаграмма путей, объединяющая три латентных (А, В, С) и две наблюдаемых
Структурное моделирование
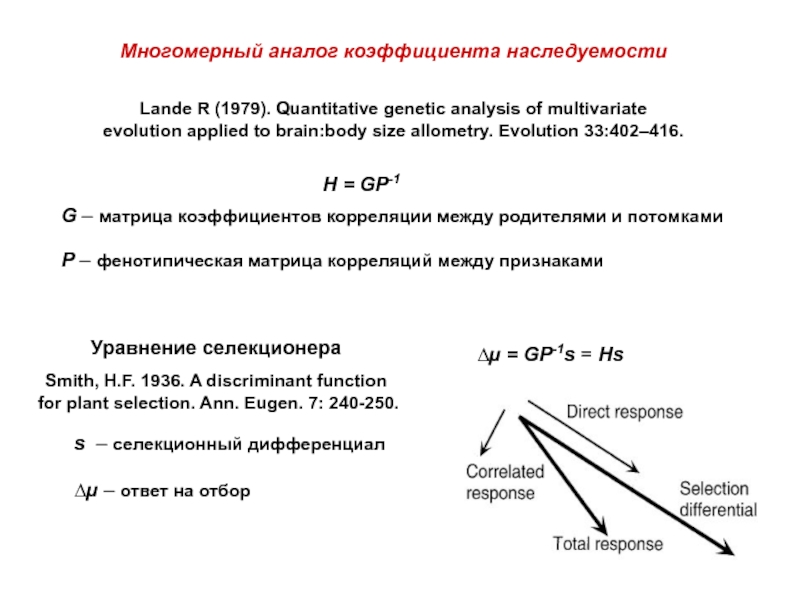
Слайд 30H = GP-1
Многомерный аналог коэффициента наследуемости
Lande R (1979). Quantitative genetic
evolution applied to brain:body size allometry. Evolution 33:402–416.
G – матрица коэффициентов корреляции между родителями и потомками
P – фенотипическая матрица корреляций между признаками
Уравнение селекционера
Smith, H.F. 1936. A discriminant function
for plant selection. Ann. Eugen. 7: 240-250.
∆µ = GP-1s = Hs
s – селекционный дифференциал
∆µ – ответ на отбор
Слайд 32
Поиск осей с максимальной наследуемостью
(в узком смысле)
Ott J, Rabinowitz D (1999).
based on heritability for combining phenotype information.
Hum Hered 49: 106–111.
Klingenberg CP, Leamy L. 2001. Quantitative genetics
of geometric shape in the mouse mandible.
Evolution 55(11): 2342–2352.
∆µ = GP-1s = Hs = λs
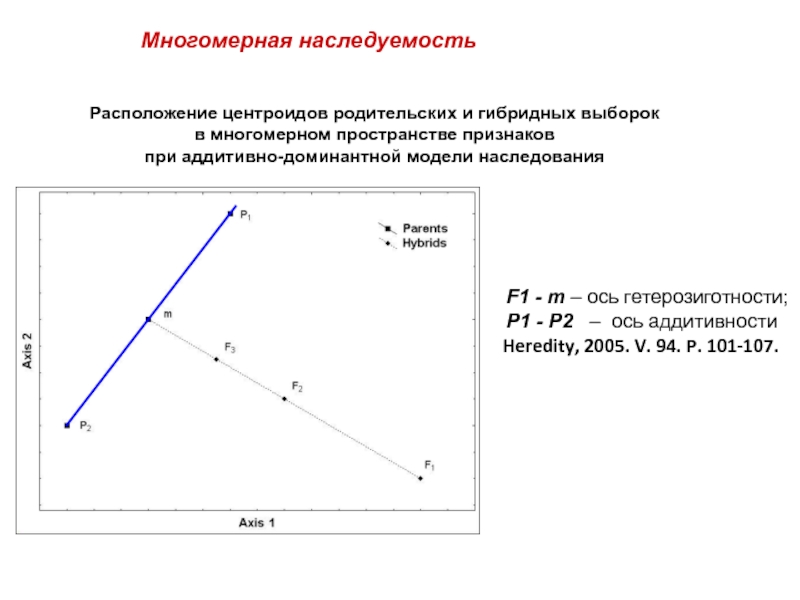
Слайд 34Расположение центроидов родительских и гибридных выборок
в многомерном пространстве признаков
при аддитивно-доминантной
F1 - m – ось гетерозиготности;
P1 - P2 – ось аддитивности
Heredity, 2005. V. 94. P. 101-107.
Многомерная наследуемость
Слайд 35F1 - F# – ось гетерозиготности H
P1 - P2 – ось
m - F# – ось эпистаза I
(F1 - m – ось гетерозиготности
в аддитивно-доминантной модели)
Расположение центроидов родительских и гибридных выборок в многомерном пространстве признаков в общем случае
(HIA-модель)
Многомерная наследуемость
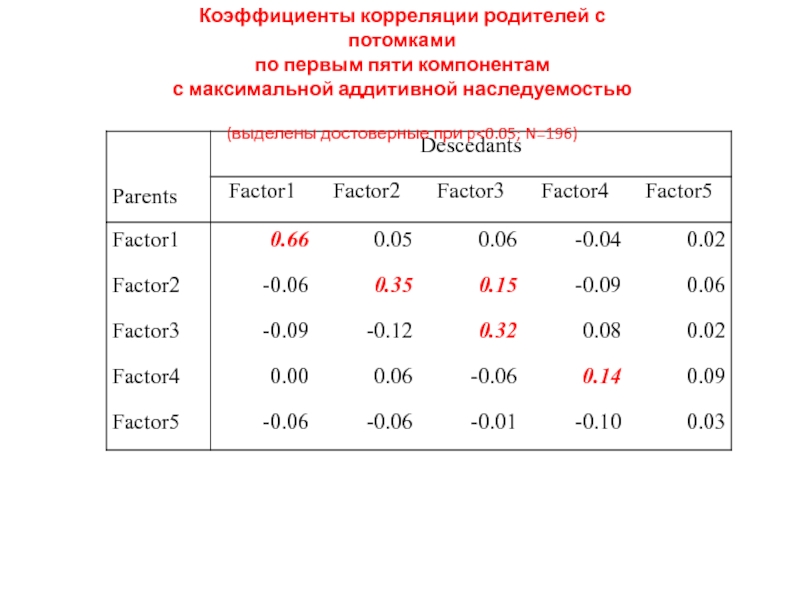
Слайд 41Коэффициенты корреляции родителей с потомками
по первым пяти компонентам
с максимальной аддитивной наследуемостью
(выделены
Слайд 42
Коэффициент наследуемости
через корреляции “родитель-потомок”:
один родитель - потомок
(в случае отсутствия
один родитель - потомок
(при ассортативности)