- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рыскин Н.М.Саратовский госуниверситетФакультет нелинейных процессов презентация
Содержание
- 1. Рыскин Н.М.Саратовский госуниверситетФакультет нелинейных процессов
- 2. Модуляционная неустойчивость
- 3. Переход к хаосу при МН магнитостатических волн
- 4. Переход к хаосу при МН магнитостатических волн в пленках ЖИГ удвоения периода разрушение квазипериодичности
- 5. Два типа неустойчивости
- 6. МН — абсолютная или конвективная?
- 7. МН — абсолютная или конвективная? Дисперсионная характеристика
- 8. Нелинейный эффект перехода от конвективной неустойчивости к абсолютной Конвективная МН
- 9. Переход к хаосу
- 10. Нелинейное уравнение Клейна–Гордона Без ограничения общности можно положить
- 11. Нелинейное уравнение Клейна–Гордона С ростом амплитуды вначале
- 12. Нелинейное уравнение Клейна–Гордона 1 — область непропускания;
- 13. Нелинейное туннелирование Newell A.C. // J. Math.
- 14. Нелинейное туннелирование а
- 15. Нелинейное туннелирование Картины пространственно-временной динамики
- 16. Нелинейная динамика МН в периодической брэгговской структуре
- 17. Численное моделирование методом FDTD Параметры структуры: толщина
- 18. Численное моделирование методом FDTD
- 19. Численное моделирование методом FDTD
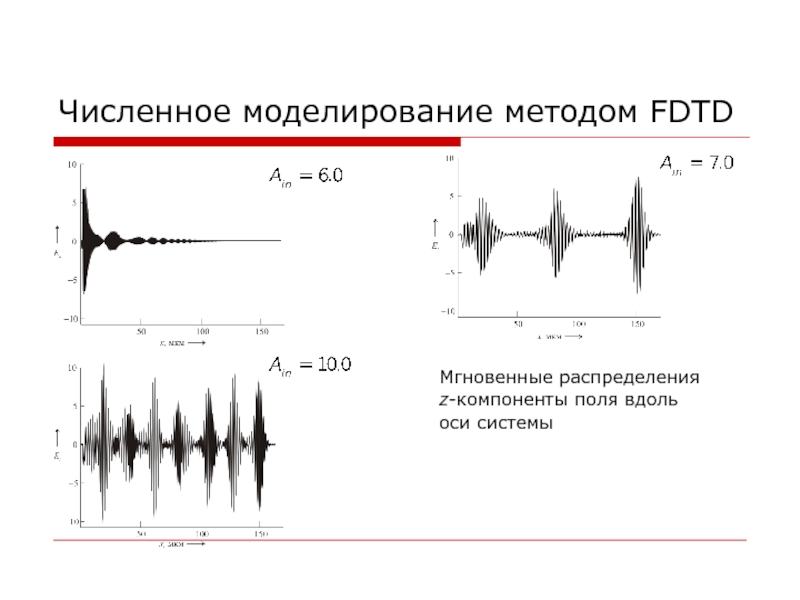
- 20. Численное моделирование методом FDTD Мгновенные распределения z-компоненты поля вдоль оси системы
Слайд 1
НЕЛИНЕЙНАЯ ДИНАМИКА
МОДУЛЯЦИОННОЙ НЕУСТОЙЧИВОСТИ
Рыскин Н.М.
Саратовский госуниверситет
Факультет нелинейных процессов
Слайд 3Переход к хаосу при МН магнитостатических волн в пленках ЖИГ
Дудко
Г.М., Казаков Г.Т., Кожевников А.В., Филимонов Ю.А. //
Письма в ЖТФ 13, 736 (1987).
Дудко Г.М., Филимонов Ю.А. // Письма в ЖТФ 15(2), 55 (1989).
Дудко Г.М., Славин А.В. // ЖТФ 31 (6), 114 (1989).
Демидов В.Е., Ковшиков Н.Г. // Письма в ЖЭТФ 66, 243 (1997).
Дудко Г.М., Филимонов Ю.А. // Письма в ЖТФ 15(2), 55 (1989).
Дудко Г.М., Славин А.В. // ЖТФ 31 (6), 114 (1989).
Демидов В.Е., Ковшиков Н.Г. // Письма в ЖЭТФ 66, 243 (1997).
Слайд 4Переход к хаосу при МН магнитостатических волн в пленках ЖИГ
удвоения периода
разрушение
квазипериодичности
Слайд 7МН — абсолютная или конвективная?
Дисперсионная характеристика для нелинейного уравнения Шредингера в
случае конвективной (1) и абсолютной (2) МН. Заштрихован диапазон волновых чисел, в котором имеет место неустойчивость
Слайд 9Переход к хаосу
б
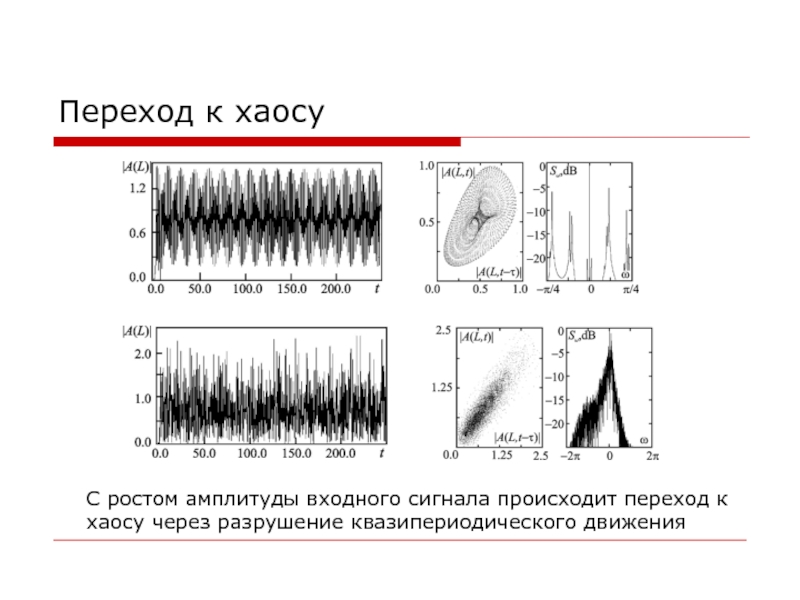
С ростом амплитуды входного сигнала происходит
переход к хаосу через разрушение квазипериодического движения
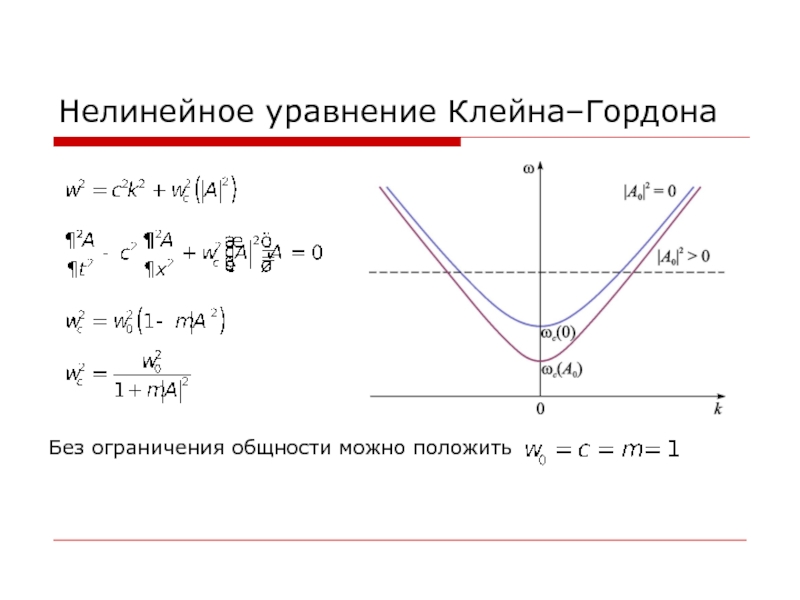
Слайд 11Нелинейное уравнение Клейна–Гордона
С ростом амплитуды вначале происходит переход от конвективной неустойчивости
к абсолютной.
Затем из-за уменьшения дисперсии происходит обратный переход к конвективной неустойчивости.
Затем из-за уменьшения дисперсии происходит обратный переход к конвективной неустойчивости.
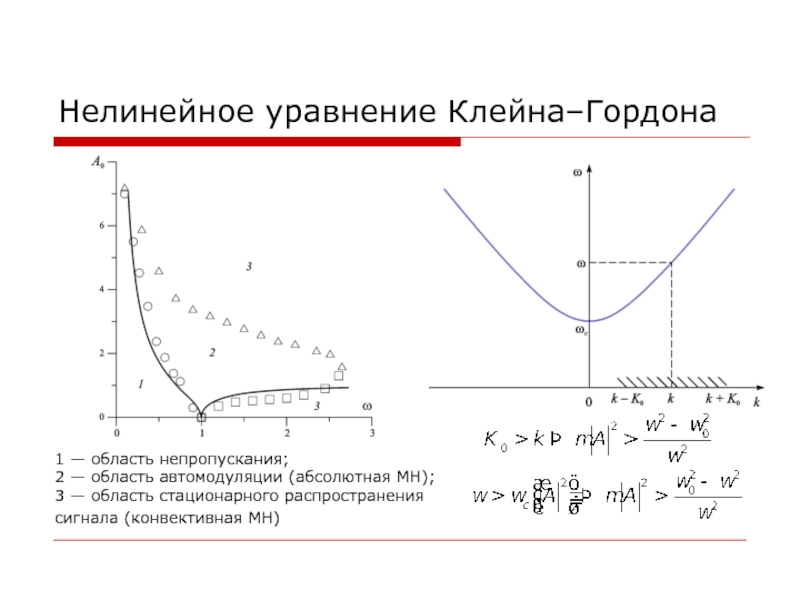
Слайд 12Нелинейное уравнение Клейна–Гордона
1 — область непропускания;
2 — область автомодуляции (абсолютная
МН);
3 — область стационарного распространения сигнала (конвективная МН)
3 — область стационарного распространения сигнала (конвективная МН)
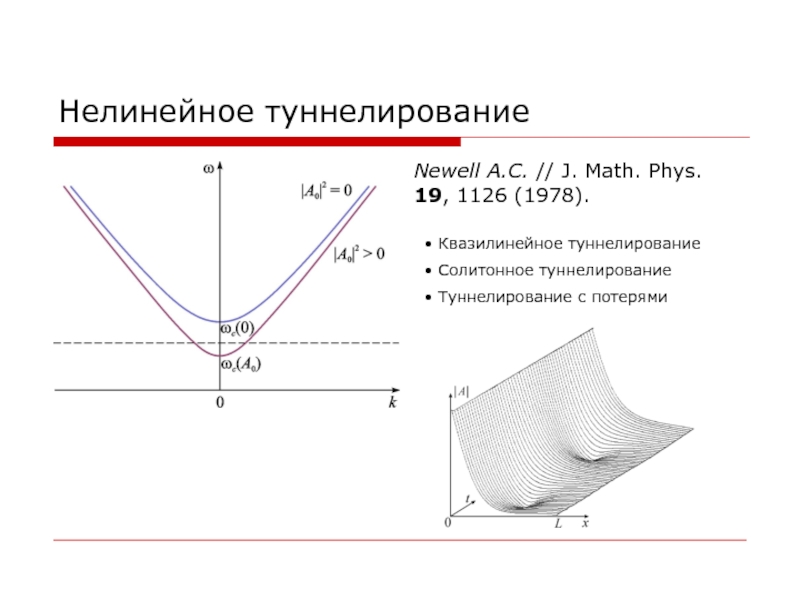
Слайд 13Нелинейное туннелирование
Newell A.C. // J. Math. Phys. 19, 1126 (1978).
Квазилинейное туннелирование
Солитонное туннелирование
Туннелирование с потерями
Солитонное туннелирование
Туннелирование с потерями
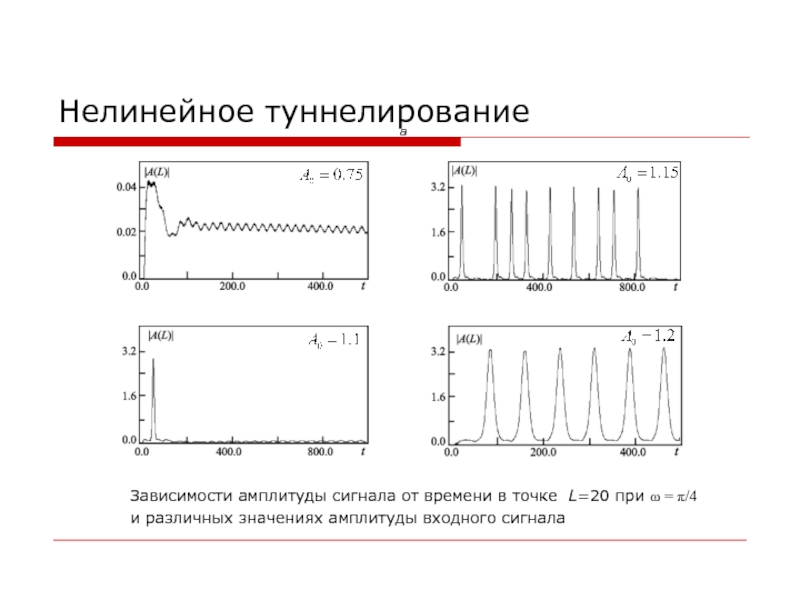
Слайд 14Нелинейное туннелирование
а
Зависимости амплитуды сигнала от времени в точке L=20
при ω = π/4 и различных значениях амплитуды входного сигнала
Слайд 17Численное моделирование методом FDTD
Параметры структуры: толщина одного слоя 0.5 мкм, число слоев
100, период структуры 1 мкм, поперечный размер слоев 1 мкм, линейная часть показателей преломления слоев n1=1.45, n2=2.0.
ПВ – подводящий волновод
Дисперсионные характеристики структуры для различных значений амплитуды входного сигнала:
1 – A=1.0, 2 – A=3.0, 3 – A=3.5