Различают два вида резонанса:
1.Резонанс в последовательной цепи или резонанс напряжений. Условия резонанса :
а) φu – φi = 0 или φ =0.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Резонанс в линейных электрических цепях презентация
Содержание
- 1. Резонанс в линейных электрических цепях
- 2. 2003г. Переменный ток 1.Резонанс в параллельной цепи
- 3. 2003г. Переменный ток XL-Xc=0, или ХL=Xc Условие
- 4. 2003г. Переменный ток Векторная диаграмма резонанса напряжений
- 5. 2003г. Переменный ток Если
- 6. 2003г. Переменный ток Частотные характеристики электрической цепи при резонансе напряжений. Фазочастотная характеристика. Частотные характеристики сопротивлений
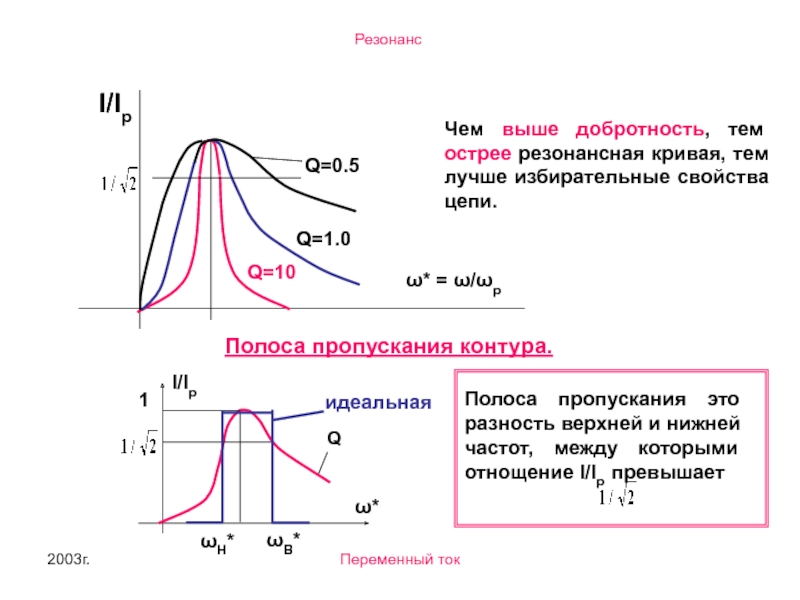
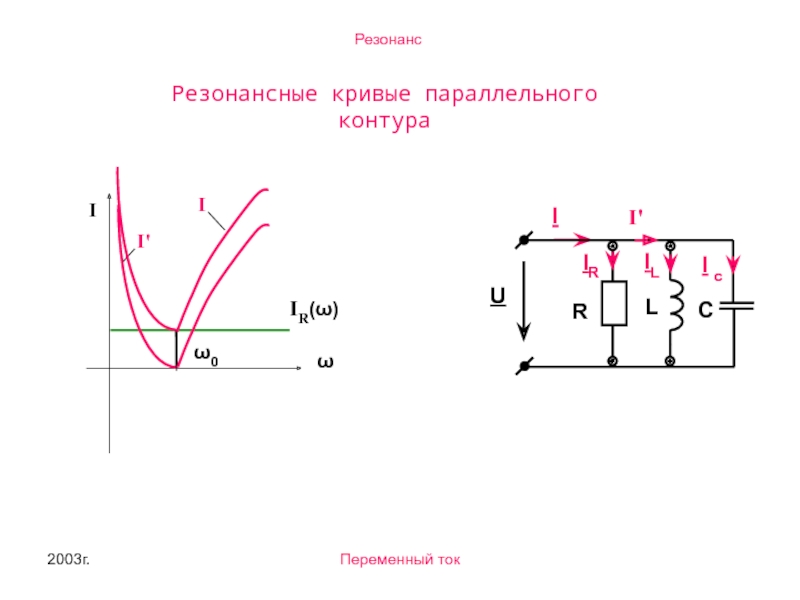
- 7. 2003г. Переменный ток Резонансные кривые последовательного контура. Q - коэффициент резонанса или добротность контура.
- 8. 2003г. Переменный ток ω* = ω/ωp Чем
- 9. 2003г. Переменный ток U L С I
- 10. 2003г.
- 11. 2003г. Переменный ток волновая проводимость
- 12. 2003г. Переменный ток IR = Ug В
- 13. 2003г. Переменный ток Векторная диаграмма цепи в
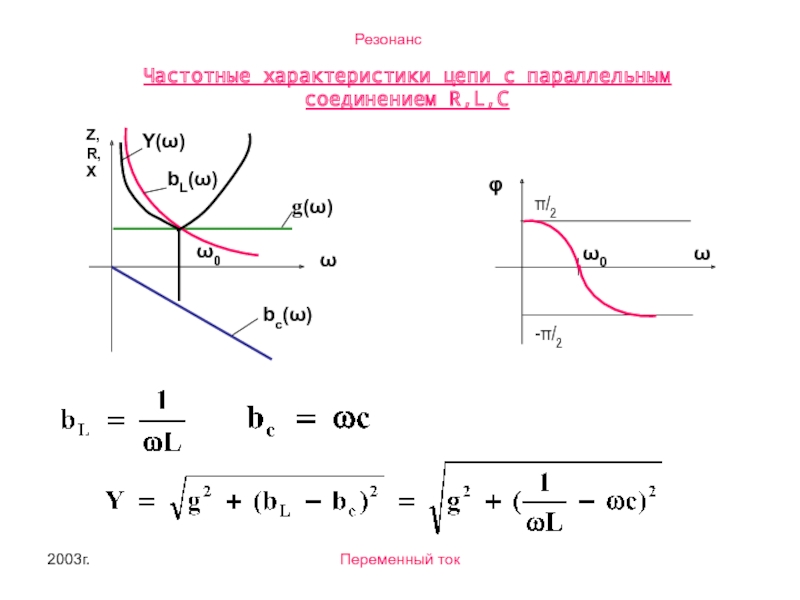
- 14. 2003г. Переменный ток Частотные характеристики цепи с параллельным соединением R,L,C
- 15. 2003г. Переменный ток U L С I
- 16. 2003г. Переменный ток Замечания к резонансным
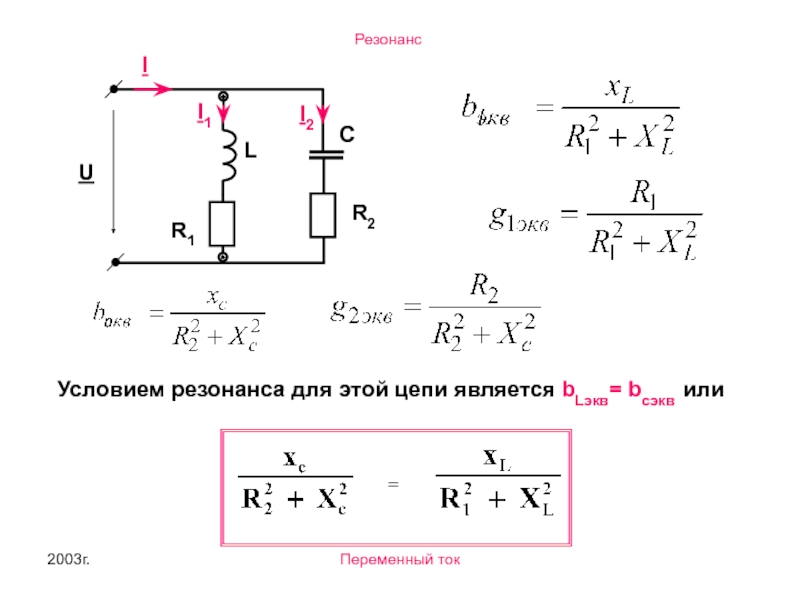
- 17. 2003г. Переменный ток 2. Резонанс токов В
- 18. 2003г. Переменный ток I R2 U L
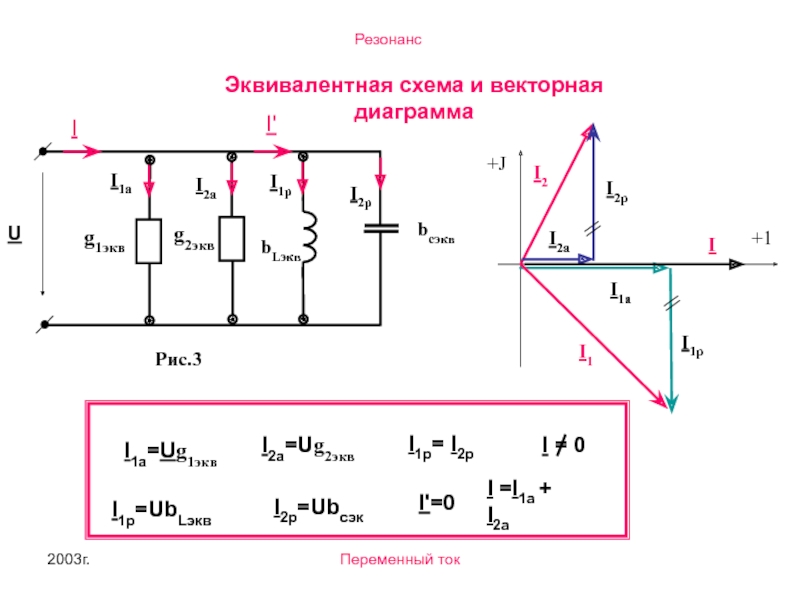
- 19. 2003г. Переменный ток Эквивалентная схема и векторная
- 20. 2003г. Переменный ток Резонанс в сложных электрических
Слайд 12003г.
Переменный ток
Резонанс в линейных электрических цепях.
В электрических цепях иногда несмотря на
Слайд 22003г.
Переменный ток
1.Резонанс в параллельной цепи или резонанс токов. Условия резонанса :
а)
в) Jm ( Y ) = 0
Резонанс в последовательной цепи или резонанс напряжений.
i(t)
L
С
u(t)
R
Z вх=R + jxL- jxc= R +j(xL- xc)=R + jx
х
По условию резоанса Jm(Z)=0
Слайд 32003г.
Переменный ток
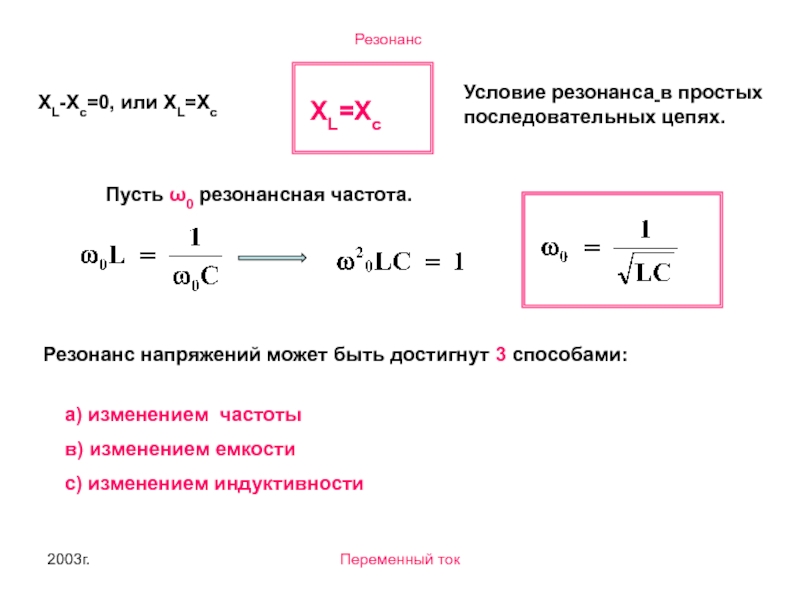
XL-Xc=0, или ХL=Xc
Условие резонанса в простых последовательных цепях.
ХL=Xc
Пусть ω0 резонансная
Резонанс напряжений может быть достигнут 3 способами:
а) изменением частоты
в) изменением емкости
с) изменением индуктивности
Слайд 42003г.
Переменный ток
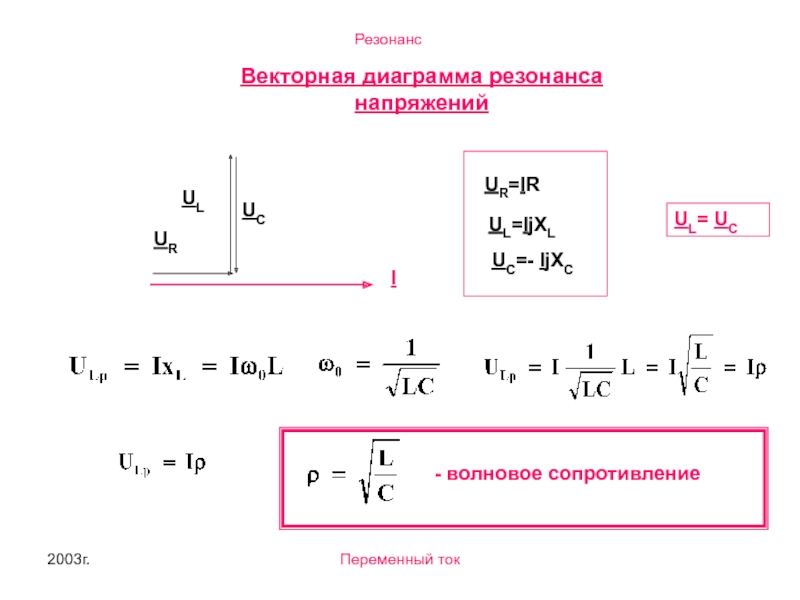
Векторная диаграмма резонанса напряжений
UR=IR
UL=IjXL
UC=- IjXC
UL= UC
- волновое сопротивление
Слайд 52003г.
Переменный ток
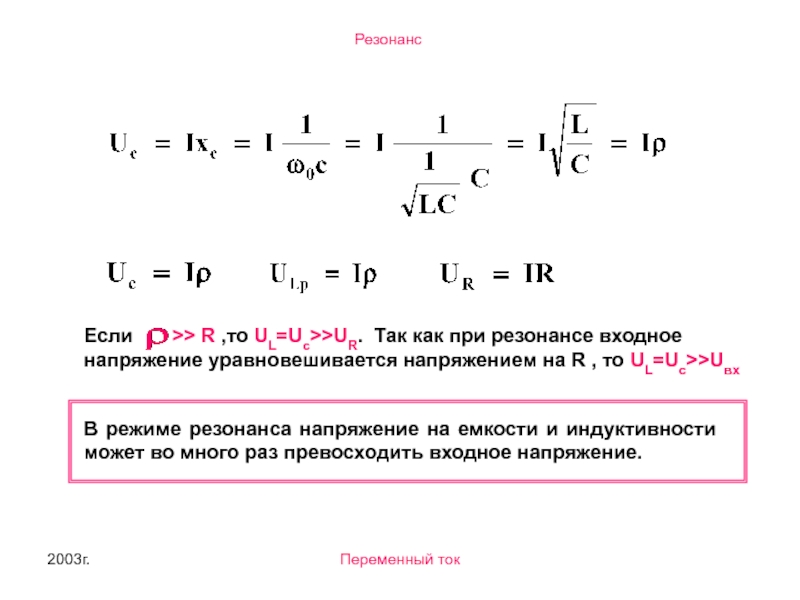
Если >> R ,то UL=Uc>>UR. Так как
В режиме резонанса напряжение на емкости и индуктивности может во много раз превосходить входное напряжение.
Слайд 62003г.
Переменный ток
Частотные характеристики электрической цепи при резонансе напряжений.
Фазочастотная характеристика.
Частотные характеристики сопротивлений
Слайд 72003г.
Переменный ток
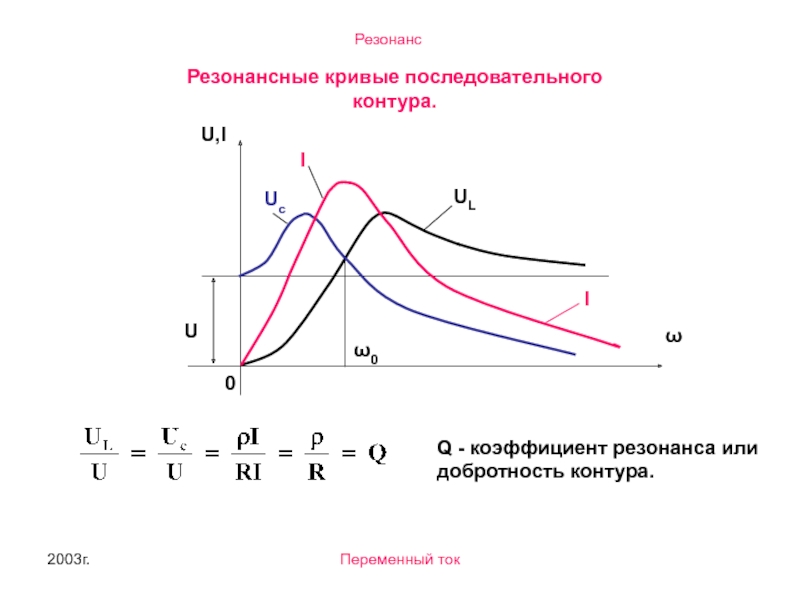
Резонансные кривые последовательного контура.
Q - коэффициент резонанса или добротность контура.
Слайд 82003г.
Переменный ток
ω* = ω/ωp
Чем выше добротность, тем острее резонансная кривая, тем
Полоса пропускания контура.
1
I/Iр
ωH*
ω*
идеальная
Q
Полоса пропускания это разность верхней и нижней частот, между которыми отнощение I/Ip превышает
Слайд 92003г.
Переменный ток
U
L
С
I
R
I R
I L
I c
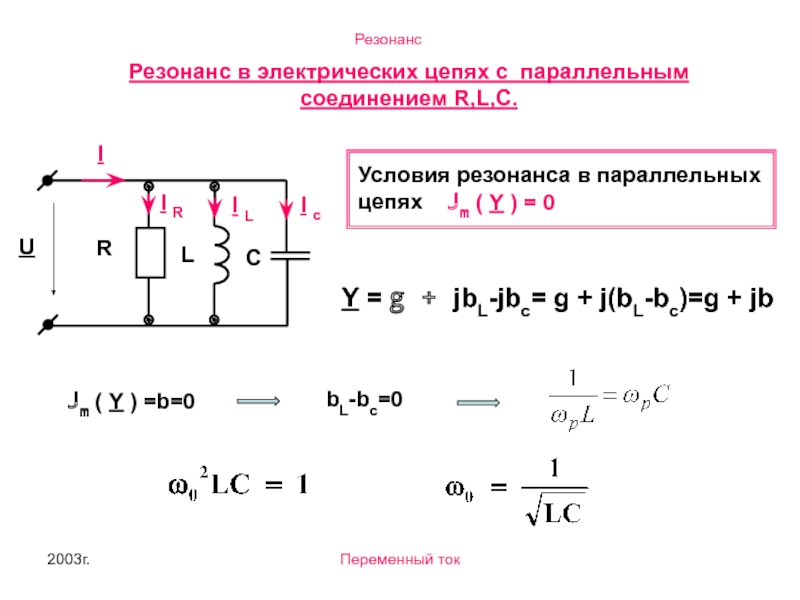
Резонанс в электрических цепях с параллельным соединением
Условия резонанса в параллельных цепях
Jm ( Y ) = 0
Y = g + jbL-jbc= g + j(bL-bc)=g + jb
Jm ( Y ) =b=0
bL-bc=0
Слайд 122003г.
Переменный ток
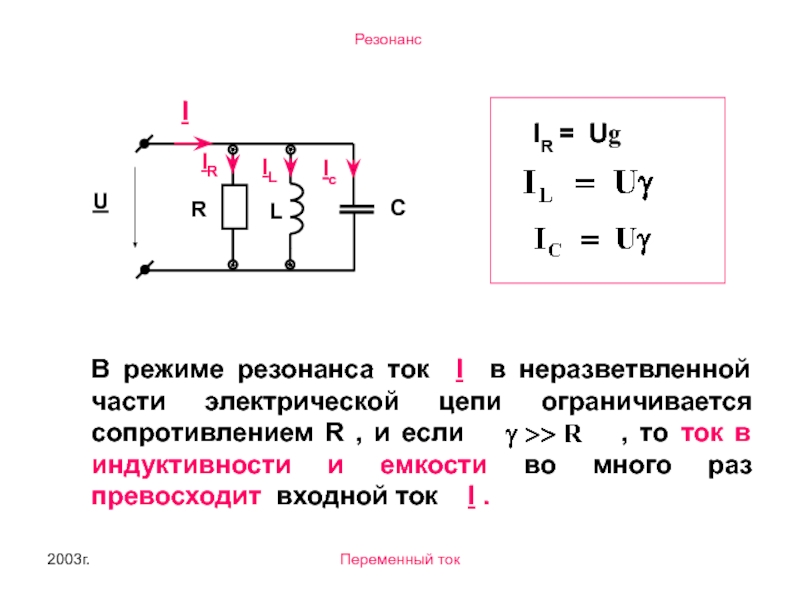
IR = Ug
В режиме резонанса ток I в неразветвленной части
Слайд 132003г.
Переменный ток
Векторная диаграмма цепи в режиме резонанаса токов
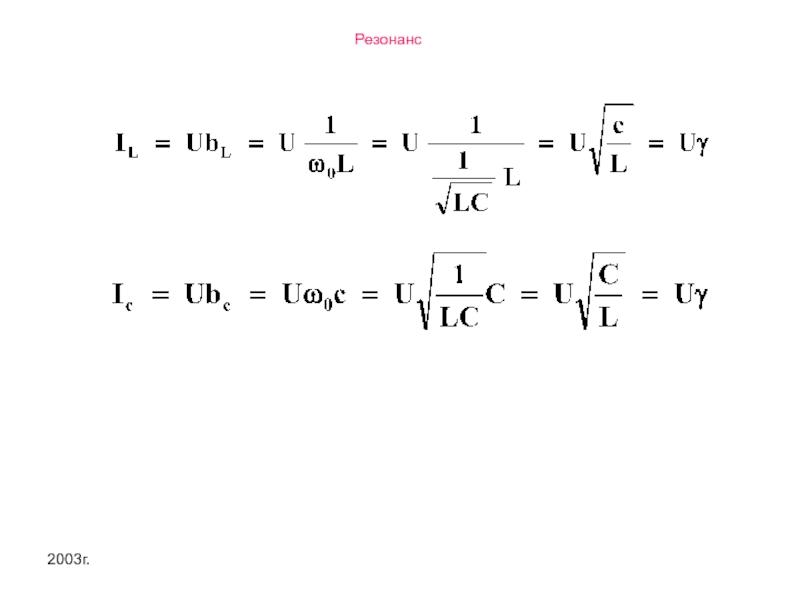
Токи в индуктивности и
Слайд 162003г.
Переменный ток
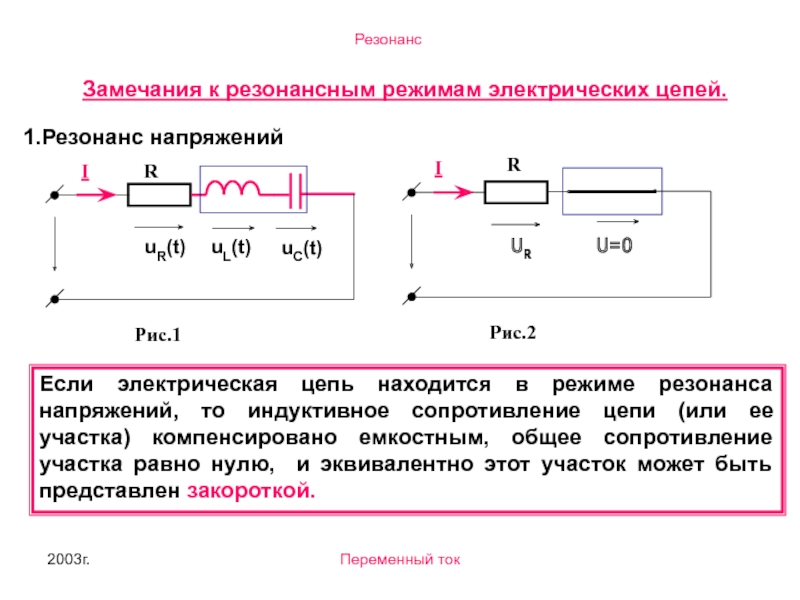
Замечания к резонансным режимам электрических цепей.
Если электрическая цепь находится в
1.Резонанс напряжений
UR
U=0
I
Рис.2
R
uR(t)
uL(t)
uC(t)
I
Рис.1
R
Слайд 172003г.
Переменный ток
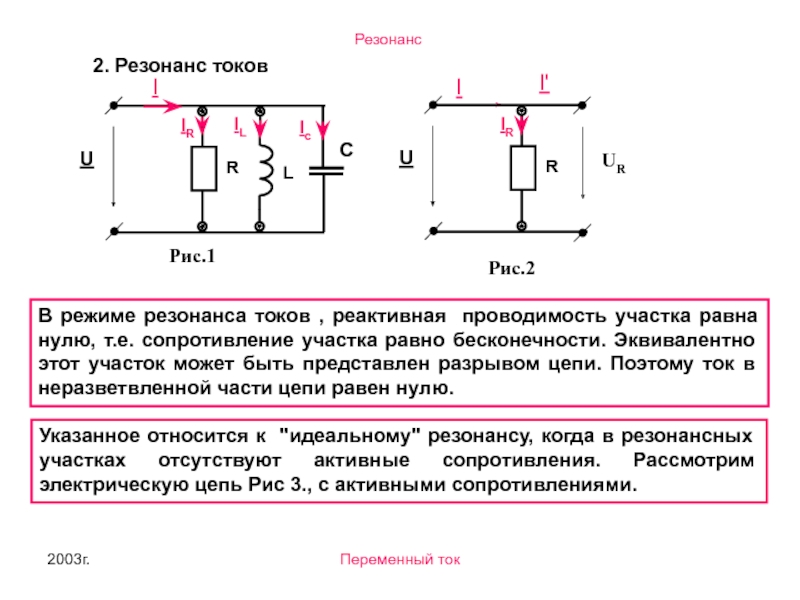
2. Резонанс токов
В режиме резонанса токов , реактивная проводимость участка
Указанное относится к "идеальному" резонансу, когда в резонансных участках отсутствуют активные сопротивления. Рассмотрим электрическую цепь Рис 3., с активными сопротивлениями.
U
I
R
IR
UR
I'
Рис.2