- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение неравенств второй степени. презентация
Содержание
- 1. Решение неравенств второй степени.
- 2. Решение неравенств второй степени. Цели:
- 3. Решение неравенств второй степени. Задачи: Повторить: -способы
- 4. Решение неравенств второй
- 5. Решение неравенств второй степени. Графическим способом
- 6. Решение неравенств второй степени. Определение: а*х²
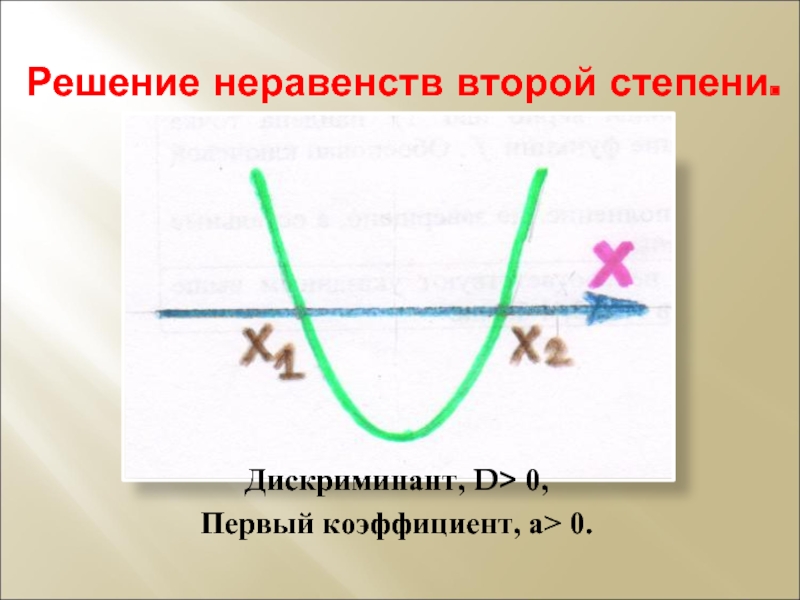
- 7. Решение неравенств второй степени. Дискриминант, D> 0, Первый коэффициент, а> 0.
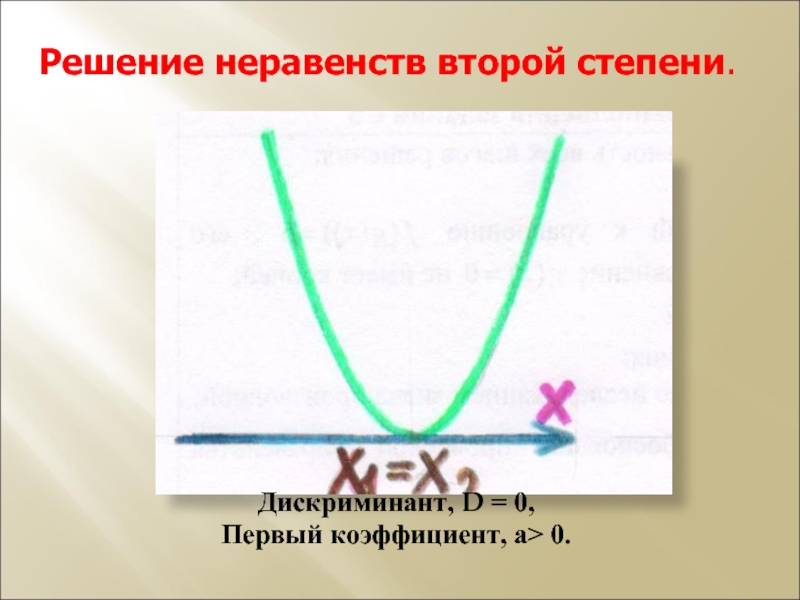
- 8. Дискриминант, D = 0, Первый коэффициент, а> 0. Решение неравенств второй степени.
- 9. Решение неравенств второй
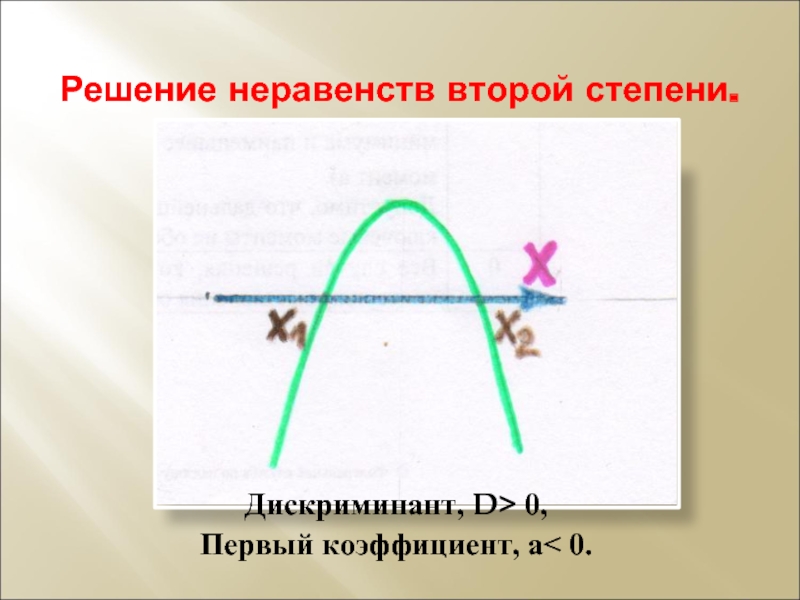
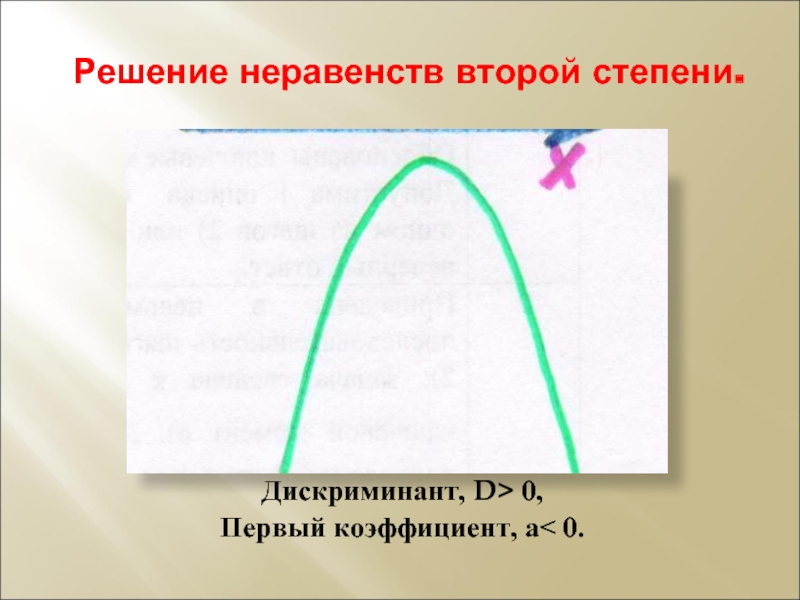
- 10. Решение неравенств второй степени. Дискриминант, D> 0, Первый коэффициент, а< 0.
- 11. Решение неравенств второй степени. Дискриминант, D = 0, Первый коэффициент, а < 0.
- 12. Решение неравенств второй степени. Дискриминант, D> 0, Первый коэффициент, а< 0.
- 13. Решение неравенств второй степени. Постановка задачи.
- 14. Решение неравенств второй степени. Смоделируем задачу.
- 15. Решение неравенств второй степени. Определить промежутки
- 16. Алгоритм решения неравенства второй степени с одной
- 17. Решение неравенств второй степени. Решите неравенство: -х²+2х+15≥0.
- 18. Решение неравенств второй степени. Решите неравенство
- 19. Решение неравенств второй степени. Домашнее задание:
Решение неравенств второй степени.
Цели: Формирование навыков решения неравенств второй степени Развитие мыслительной деятельности у учащихся. Повышение познавательной активности у учащихся. Актуализация имеющихся знаний.
Слайд 2
Решение неравенств второй степени.
Цели:
Формирование навыков решения неравенств второй степени
Развитие мыслительной деятельности
у учащихся.
Повышение познавательной активности у учащихся.
Актуализация имеющихся знаний.
Повышение познавательной активности у учащихся.
Актуализация имеющихся знаний.
Слайд 3Решение неравенств второй степени.
Задачи:
Повторить:
-способы решение квадратных уравнений различными способами, в том
числе с использованием ИКТ.
Сформулировать определение неравенства второй степени с одной переменной.
Разрешить задачу, возникшую при строительстве магазина частным предпринимателем ( с использованием ИКТ)
Перевести суть графического способа решения неравенств на аналитический.
Сформулировать алгоритм решения неравенств второй степени аналитическим способом.
Закрепить навыки решения неравенства второй степени аналитическим способом
Сформулировать определение неравенства второй степени с одной переменной.
Разрешить задачу, возникшую при строительстве магазина частным предпринимателем ( с использованием ИКТ)
Перевести суть графического способа решения неравенств на аналитический.
Сформулировать алгоритм решения неравенств второй степени аналитическим способом.
Закрепить навыки решения неравенства второй степени аналитическим способом
Слайд 4
Решение неравенств второй степени.
Решите квадратное уравнение х2-
2∙х - 8=0
( четыре способа решения квадратных уравнений 4 ученика показывают у доски)
а) разложением на множители;
б) выделением квадрата двучлена;
в) по формулам;
г) по теореме Виета;
д) графическим способом –
с использованием ИКТ.
( четыре способа решения квадратных уравнений 4 ученика показывают у доски)
а) разложением на множители;
б) выделением квадрата двучлена;
в) по формулам;
г) по теореме Виета;
д) графическим способом –
с использованием ИКТ.
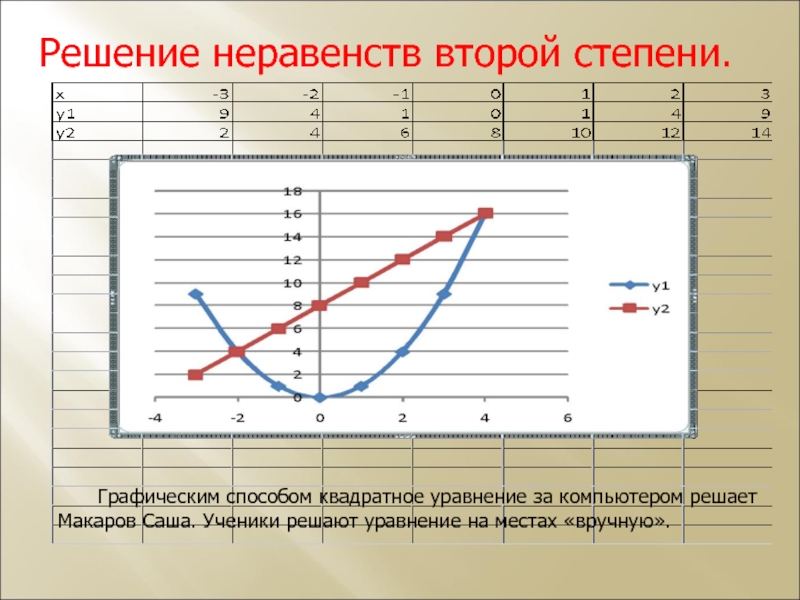
Слайд 5Решение неравенств второй степени.
Графическим способом квадратное уравнение за компьютером решает Макаров
Саша. Ученики решают уравнение на местах «вручную».
Слайд 6Решение неравенств второй степени.
Определение:
а*х² +в*х +с≥0
а*х² +в*х +с>0
а*х² +в*х +с≤0
а*х² + в*х+с<0
Слайд 13Решение неравенств второй степени.
Постановка задачи.
Некий мистер Х, решив заняться предпринимательской деятельностью, оформил в банке кредит, чтобы купить участок земли и построить на нем магазин. Оказалось, что соблюдая правила пожарной безопасности и санитарно - гигиенических нормы, он имеет право построить на своём участке магазин площадью не более 60 м 2. Какой может быть меньшая сторона здания прямоугольной формы, если по проекту архитектора большая сторона здания должна быть на 7 м больше другой?
Слайд 14Решение неравенств второй степени.
Смоделируем задачу.
Пусть х –длина меньшей стороны прямоугольника,
поэтому значение переменной х>0, тогда большая сторона – (х+7) . Площадь такого прямоугольника будет равна х ∙ (х + 7) 2 , что по условию составляет не более 60 м2.
Получим неравенство х ∙ (х + 7) ≤60,
х2+7∙х- 60≤0.
Решим неравенство с помощью графика квадратичной функции у = х²+7*х+60 .
Получим неравенство х ∙ (х + 7) ≤60,
х2+7∙х- 60≤0.
Решим неравенство с помощью графика квадратичной функции у = х²+7*х+60 .
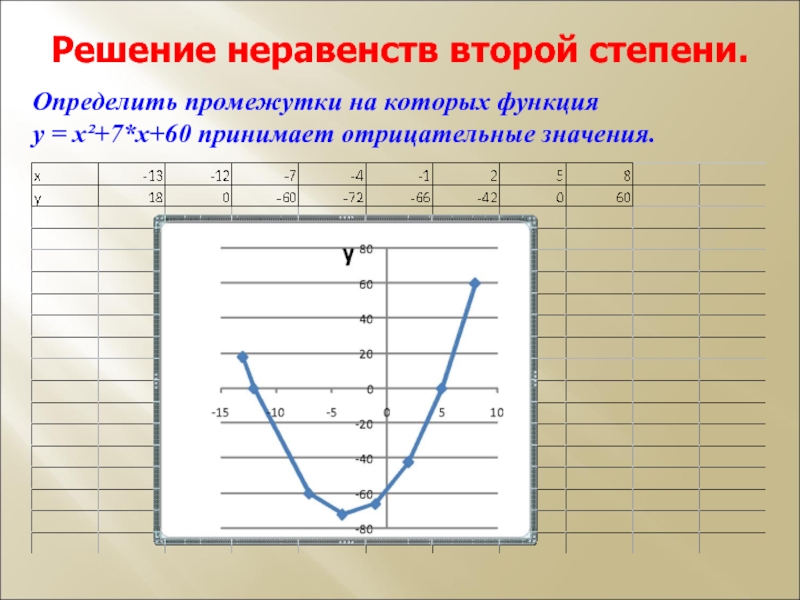
Слайд 15Решение неравенств второй степени.
Определить промежутки на которых функция
у = х²+7*х+60 принимает отрицательные значения.
Слайд 16Алгоритм решения неравенства второй степени с одной переменной.
Найти корни квадратного трехчлена;
Отметить
их на координатной прямой;
Схематично изобразить параболу, с учетом направления ветвей.
Спроектировать нужные фрагменты графика на прямую.
Записать ответ.
Схематично изобразить параболу, с учетом направления ветвей.
Спроектировать нужные фрагменты графика на прямую.
Записать ответ.
Решение неравенств второй степени.
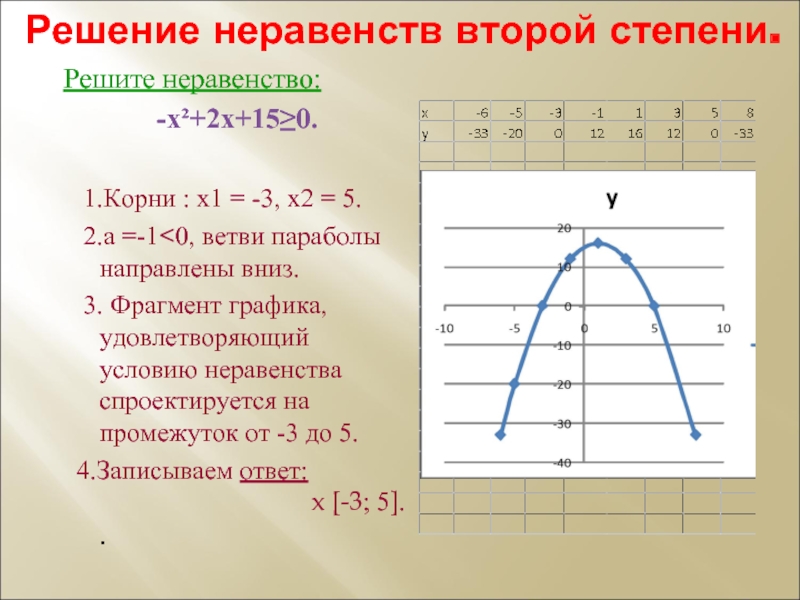
Слайд 17Решение неравенств второй степени.
Решите неравенство:
-х²+2х+15≥0.
1.Корни : х1 =
-3, х2 = 5.
2.а =-1<0, ветви параболы направлены вниз.
3. Фрагмент графика, удовлетворяющий условию неравенства спроектируется на промежуток от -3 до 5.
4.Записываем ответ: x [-3; 5]. .
2.а =-1<0, ветви параболы направлены вниз.
3. Фрагмент графика, удовлетворяющий условию неравенства спроектируется на промежуток от -3 до 5.
4.Записываем ответ: x [-3; 5]. .
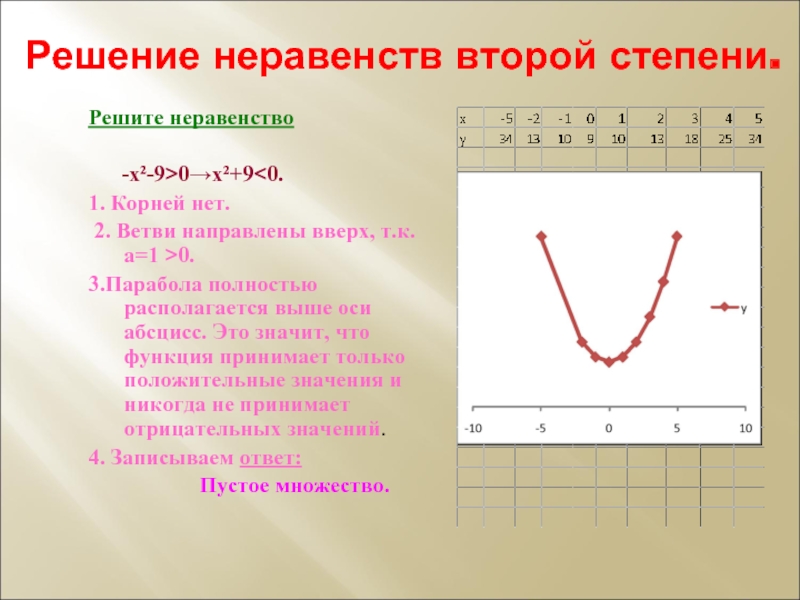
Слайд 18Решение неравенств второй степени.
Решите неравенство
-х²-9>0→х²+9
нет.
2. Ветви направлены вверх, т.к. а=1 >0.
3.Парабола полностью располагается выше оси абсцисс. Это значит, что функция принимает только положительные значения и никогда не принимает отрицательных значений.
4. Записываем ответ:
Пустое множество.
2. Ветви направлены вверх, т.к. а=1 >0.
3.Парабола полностью располагается выше оси абсцисс. Это значит, что функция принимает только положительные значения и никогда не принимает отрицательных значений.
4. Записываем ответ:
Пустое множество.
Слайд 19Решение неравенств второй степени.
Домашнее задание:
1) п.13 (прочитать примеры, выучить алгоритм решения
неравенства второй степени).
2)№№305, 324
2)№№305, 324
