отношениями действия.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реляционная алгебра презентация
Содержание
- 1. Реляционная алгебра
- 2. Операции реляционной алгебры Кодда Операции реляционной
- 3. Унарные и бинарные операции Операция реляционной алгебры
- 4. Совместимость структур отношений Совместимость структур отношений
- 5. Объединение Объединение (A UNION B)
- 6. Пример объединения R1 R2
- 7. R1 UNION R2
- 8. Пересечение А INTERSECT В Результат пересечения включает
- 9. Результат пересечения R1 INTERSECT R2
- 10. Вычитание А MINUS B В
- 11. Результат вычитания R1 MINUS R2
- 12. Произведение R1 TIMES R2
- 13. Произведение
- 14. Выборка Результатом выборки является отношение
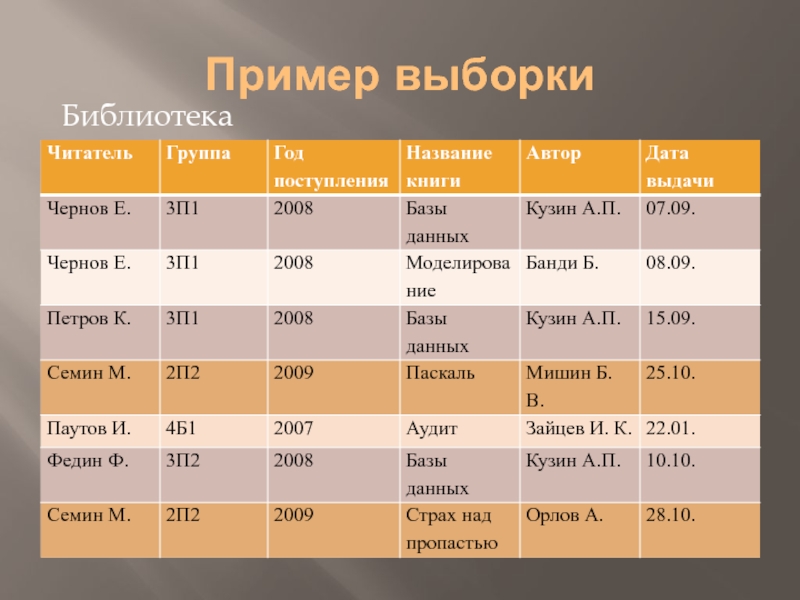
- 15. Пример выборки Библиотека
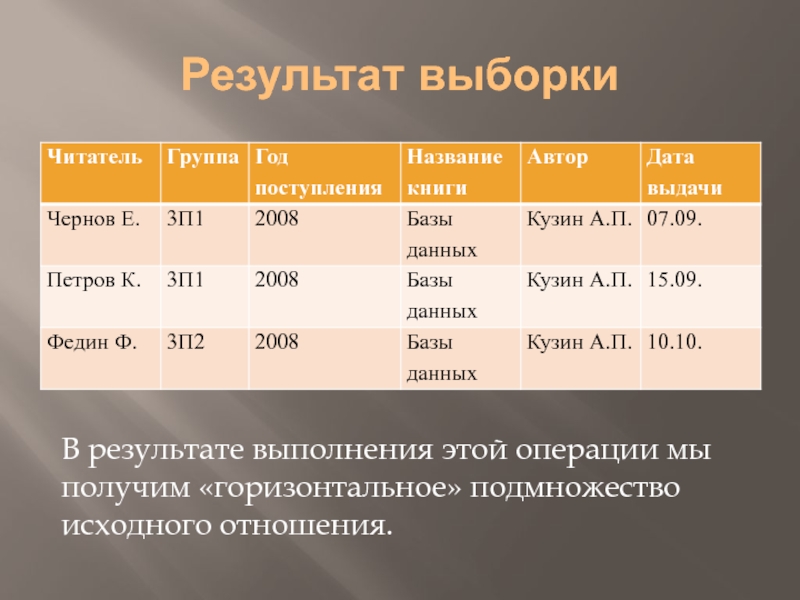
- 16. Результат выборки В результате выполнения этой операции мы получим «горизонтальное» подмножество исходного отношения.
- 17. Проекция Результатом проекции является отношение
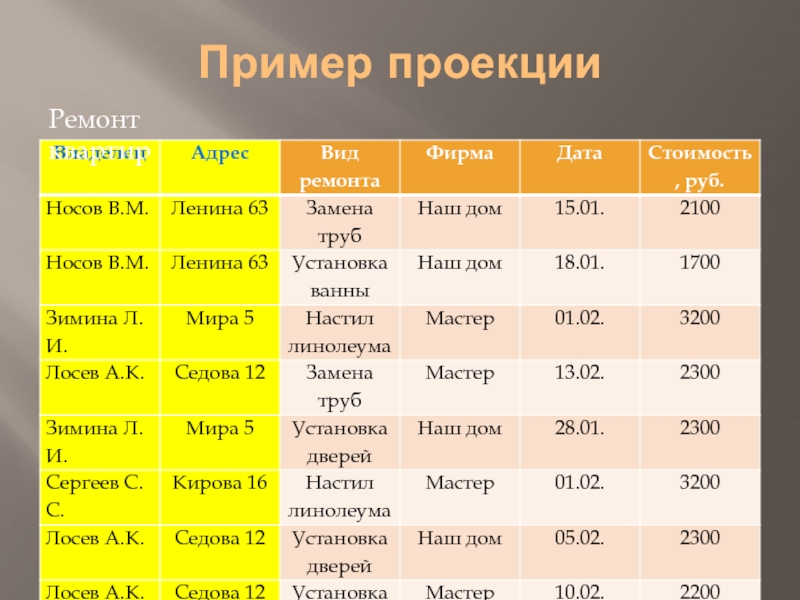
- 18. Пример проекции Ремонт квартир
- 19. Результат проекции Результатом операции ПРОЕКЦИЯ будет «вертикальное»
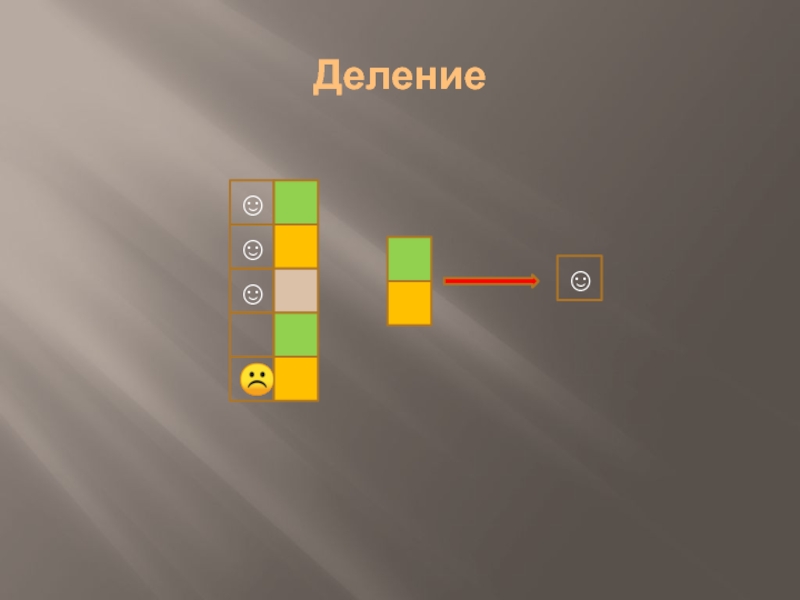
- 20. Деление R1 DIVIDEBY R2 У операции
- 21. Деление
- 22. Пример операции деления Ведомость Результат Критерий
- 23. Соединение (естественное) R1 JOIN R2 Операция
- 24. Соединение (естественное) Схема
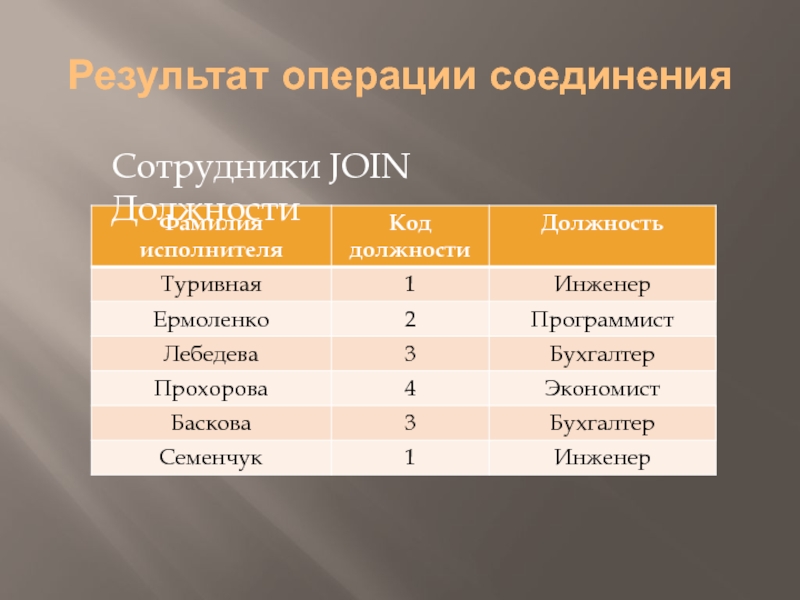
- 25. Пример соединения Сотрудники Должности
- 26. Результат операции соединения Сотрудники JOIN Должности
- 27. Задание №1 Даны исходные отношения А В
- 28. Найти результаты выполнения операций реляционной алгебры а)
- 29. A INSERSECT B A MINUS B
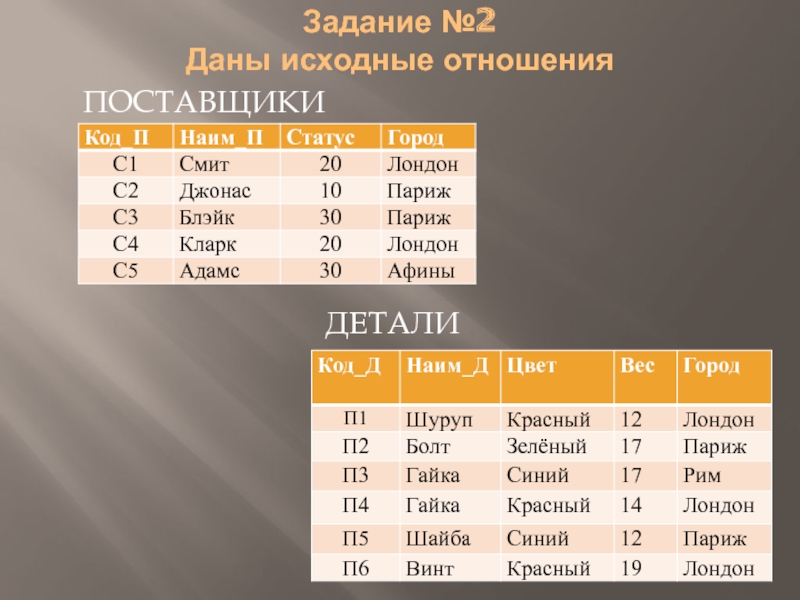
- 30. Задание №2 Даны исходные отношения ПОСТАВЩИКИ ДЕТАЛИ
- 31. Найти результаты выполнения операций Выборка всех
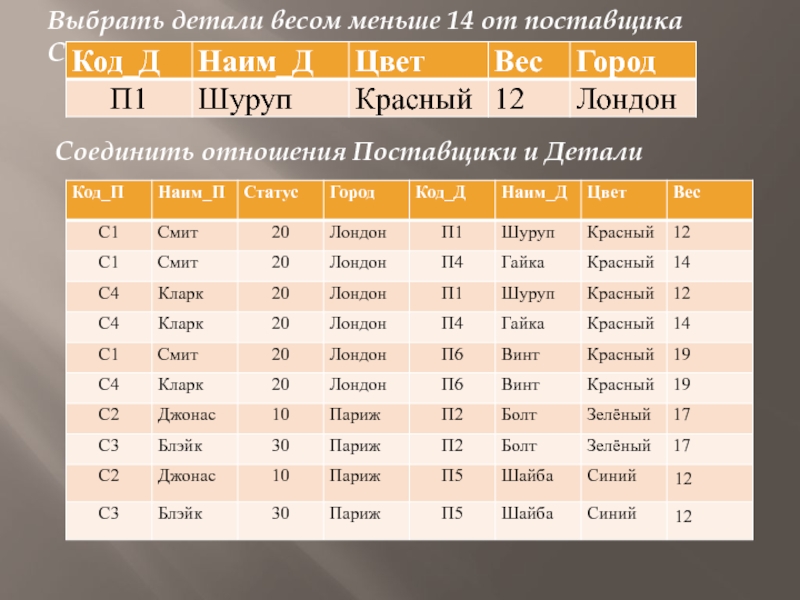
- 32. Выбрать детали весом меньше 14 от поставщика
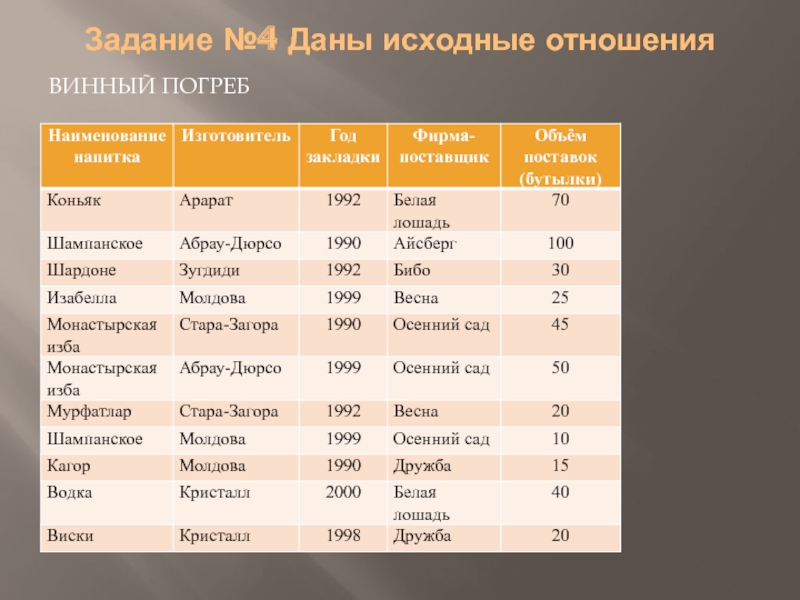
- 33. Задание №4 Даны исходные отношения ВИННЫЙ ПОГРЕБ
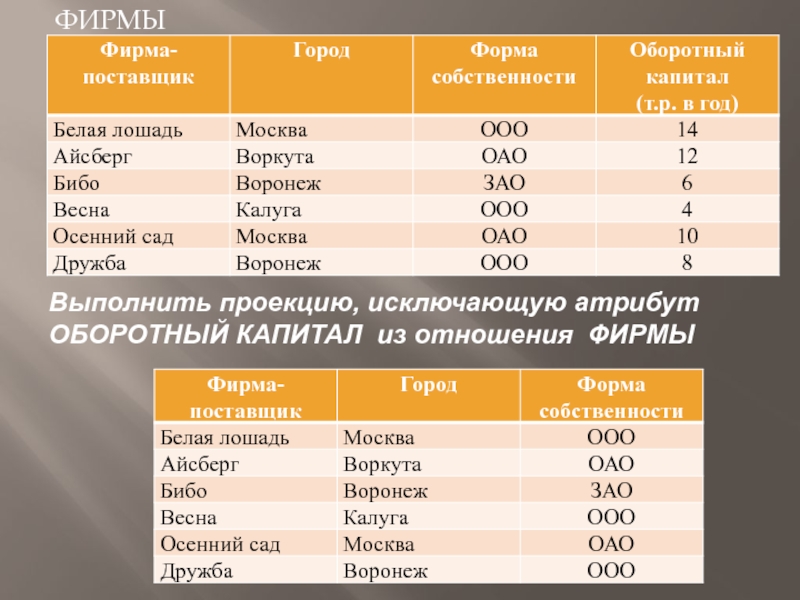
- 34. ФИРМЫ Выполнить проекцию, исключающую атрибут ОБОРОТНЫЙ КАПИТАЛ из отношения ФИРМЫ
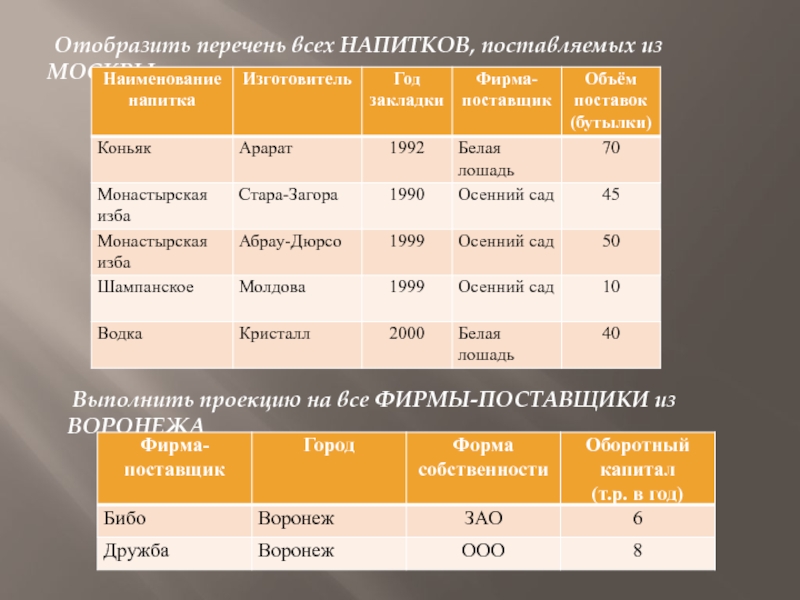
- 35. Отобразить перечень всех НАПИТКОВ, поставляемых из
- 36. САМОСТОЯТЕЛЬНО: Отобразить все напитки изготовителя АБРАУ-ДЮРСО,
Операции реляционной алгебры Кодда Операции реляционной алгебры Кодда можно разделить на две группы: базовые теоретико-множественные и специальные реляционные. Первая группа операций включает в себя классические операции теории множеств: объединение, разность,
Слайд 1РЕЛЯЦИОННАЯ АЛГЕБРА
Реляционная алгебра - теоретический язык запросов, наглядно описывающий выполняемые над
Слайд 2Операции реляционной алгебры Кодда
Операции реляционной алгебры Кодда можно разделить на
две группы: базовые теоретико-множественные и специальные реляционные. Первая группа операций включает в себя классические операции теории множеств: объединение, разность, пересечение и произведение.
Вторая группа представляет собой развитие обычных теоретико-множественных операций в направлении к реальным задачам манипулирования данными, в ее состав входят следующие операции: проекция, селекция, деление и соединение.
Вторая группа представляет собой развитие обычных теоретико-множественных операций в направлении к реальным задачам манипулирования данными, в ее состав входят следующие операции: проекция, селекция, деление и соединение.
Слайд 3Унарные и бинарные операции
Операция реляционной алгебры может выполняться
над одним отношением
(например, проекция), унарной
над двумя отношениями (например, объединение) такая операция называется бинарной.
При выполнении бинарной операции участвующие в операциях отношения должны быть совместимы по структуре.
над двумя отношениями (например, объединение) такая операция называется бинарной.
При выполнении бинарной операции участвующие в операциях отношения должны быть совместимы по структуре.
Слайд 4Совместимость структур отношений
Совместимость структур отношений означает совместимость имен атрибутов и
типов соответствующих доменов. Частным случаем совместимости является идентичность (совпадение).
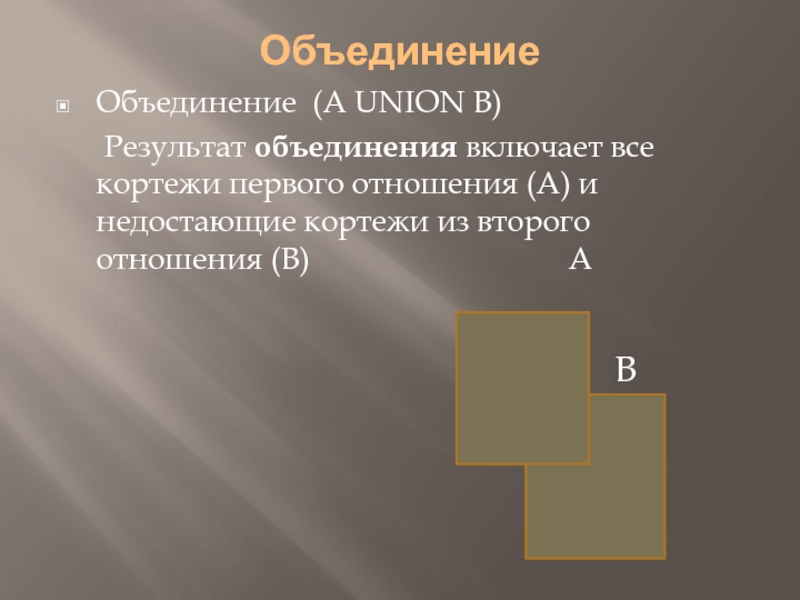
Слайд 5Объединение
Объединение (A UNION B)
Результат объединения включает все кортежи первого
отношения (А) и недостающие кортежи из второго отношения (В) А
В
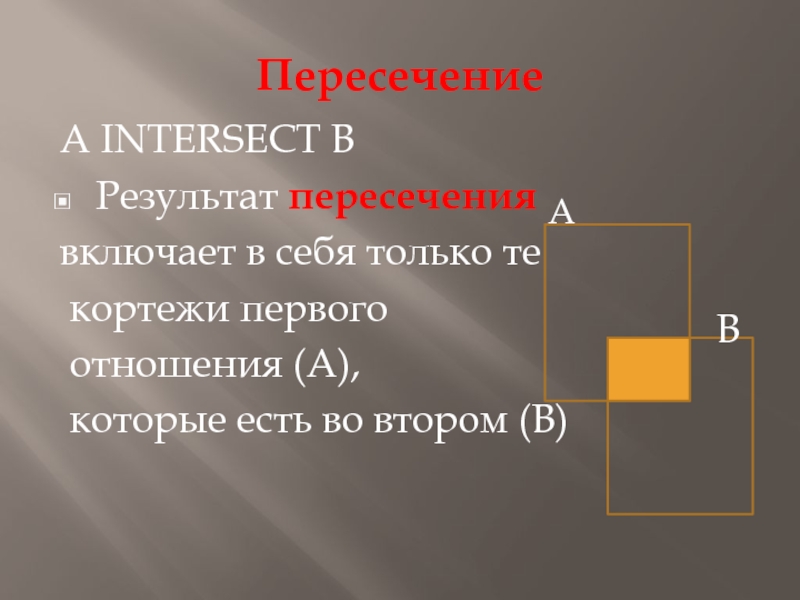
Слайд 8Пересечение
А INTERSECT В
Результат пересечения
включает в себя только те
кортежи первого
отношения
(А),
которые есть во втором (В)
которые есть во втором (В)
А
В
Слайд 10
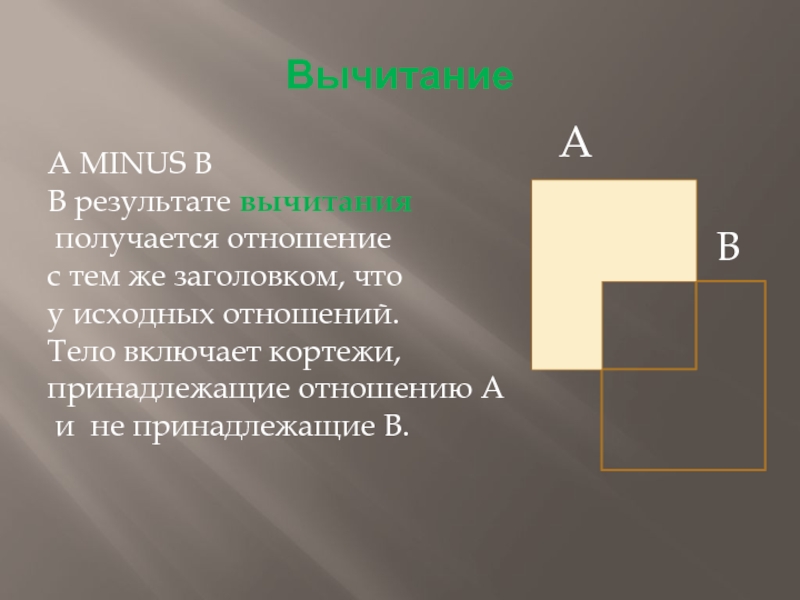
Вычитание
А MINUS B
В результате вычитания
получается отношение
с тем же
заголовком, что
у исходных отношений.
Тело включает кортежи,
принадлежащие отношению А
и не принадлежащие В.
у исходных отношений.
Тело включает кортежи,
принадлежащие отношению А
и не принадлежащие В.
А
В
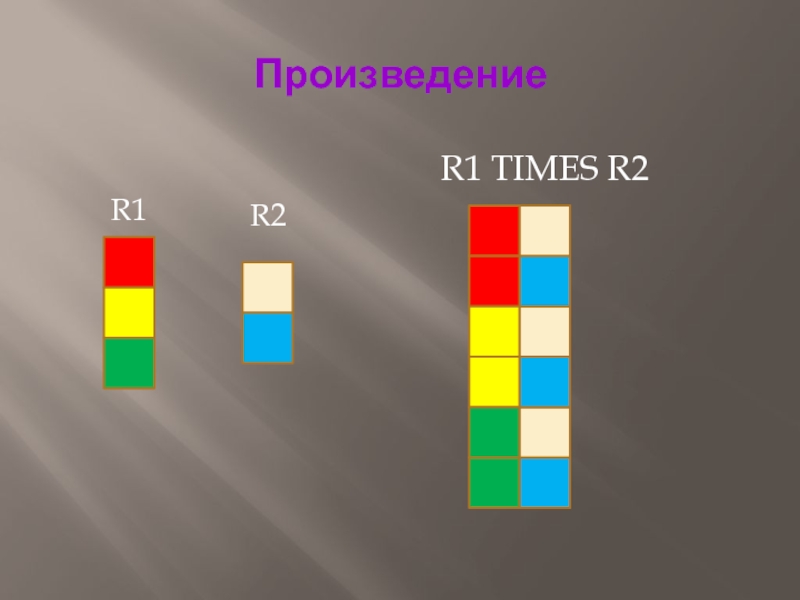
Слайд 12Произведение
R1 TIMES R2
При выполнении прямого произведения двух отношений
производится отношение, кортежи которого являются конкатенацией (сцеплением) кортежей первого и второго операндов
Слайд 14
Выборка
Результатом выборки является отношение с тем же заголовком, что и исходное
отношение (А);
тело содержит множество
кортежей исходного
отношения (А),
для которых проверка
условия дает результат
истина. (A WHERE f)
тело содержит множество
кортежей исходного
отношения (А),
для которых проверка
условия дает результат
истина. (A WHERE f)
А
Слайд 16Результат выборки
В результате выполнения этой операции мы получим «горизонтальное» подмножество исходного
отношения.
Слайд 17
Проекция
Результатом проекции является отношение с заголовком, содержащим
атрибуты, на которые
выполняется
проекция;
тело содержит множество
кортежей исходного
отношения (А), исключая
дубликаты (А [X, Y,..., Z])
A
Слайд 19Результат проекции
Результатом операции ПРОЕКЦИЯ будет «вертикальное» подмножество данного отношения, т.е. подмножество,
получаемое исключением всех атрибутов, не указанных в списке атрибутов, и последующим исключением дублирующих кортежей.( Ремонт квартир [Владелец, Адрес])
Слайд 20Деление
R1 DIVIDEBY R2
У операции реляционного деления два операнда - бинарное
и унарное отношения. Результирующее отношение состоит из одноатрибутных кортежей, включающих значения первого атрибута кортежей первого операнда таких, что множество значений второго атрибута (при фиксированном значении первого атрибута) совпадает со множеством значений второго операнда.
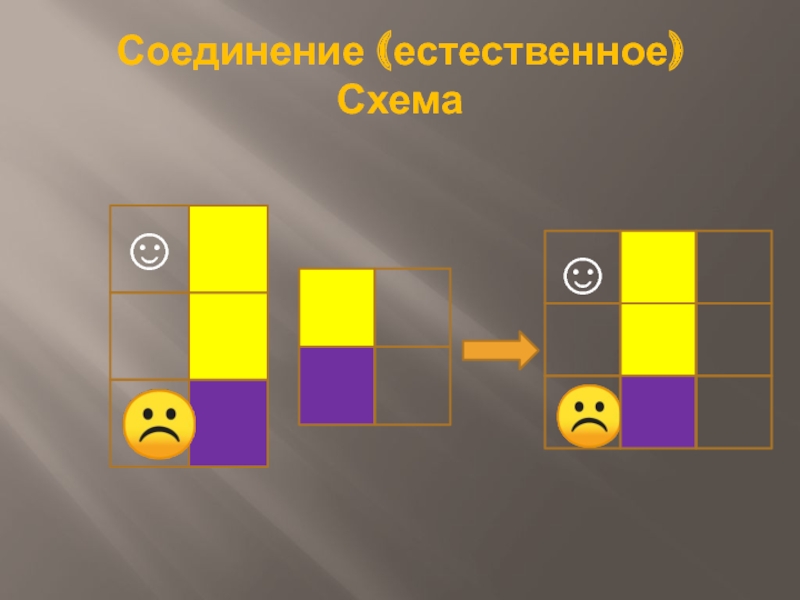
Слайд 23Соединение (естественное)
R1 JOIN R2
Операция естественного соединения применяется к двум отношениям, имеющим
общий атрибут (простой или составной). Этот атрибут в отношениях имеет одно и то же имя (совокупность имен) и определен на одном и том же домене (доменах).
Результатом операции естественного соединения является отношение R, которое представляет собой проекцию соединения отношений R1 и R2 по общему атрибуту на объединенную совокупность атрибутов обоих отношений.
Результатом операции естественного соединения является отношение R, которое представляет собой проекцию соединения отношений R1 и R2 по общему атрибуту на объединенную совокупность атрибутов обоих отношений.
Слайд 28Найти результаты выполнения операций реляционной алгебры
а) Объединение (A UNION B)
б) Пересечение
(A INSERSECT B)
в) Вычитание (A MINUS B)
A UNION B
в) Вычитание (A MINUS B)
A UNION B
Слайд 31Найти результаты выполнения операций
Выборка всех поставщиков, поставляющих детали красного цвета
Проекция,
исключающая атрибут ВЕС из отношения ДЕТАЛИ
Слайд 35 Отобразить перечень всех НАПИТКОВ, поставляемых из МОСКВЫ
Выполнить проекцию на
все ФИРМЫ-ПОСТАВЩИКИ из ВОРОНЕЖА
Слайд 36САМОСТОЯТЕЛЬНО:
Отобразить все напитки изготовителя АБРАУ-ДЮРСО, поставляемые фирмами,
ОБОРОТНЫЙ КАПИТАЛ которых >
10 т.р.
Выполнить проекцию на все НАПИТКИ, изготовленные раньше 1992 года и наименование которых начинается с буквы «К»
Отобразить все напитки, поставляемые фирмами с ФОРМОЙ СОБСТВЕННОСТИ «ОАО»
Выполнить проекцию на все НАПИТКИ, изготовленные раньше 1992 года и наименование которых начинается с буквы «К»
Отобразить все напитки, поставляемые фирмами с ФОРМОЙ СОБСТВЕННОСТИ «ОАО»
