- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольник, ромб, квадрат презентация
Содержание
- 1. Прямоугольник, ромб, квадрат
- 2. I. Устная работа 1) Существует ли
- 3. II. Новый материал Изобразим параллелограмм ABCD,
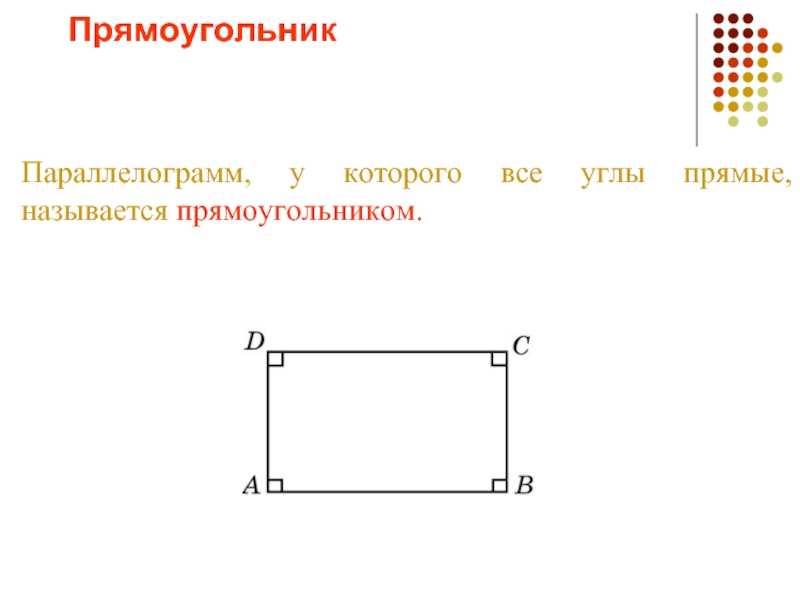
- 4. Прямоугольник Параллелограмм, у которого все углы прямые, называется прямоугольником.
- 5. - Обладает ли прямоугольник всеми свойствами
- 6. Свойство прямоугольника. Диагонали прямоугольника равны. Дано:
- 7. Задания - В четырехугольнике ABCD диагонали
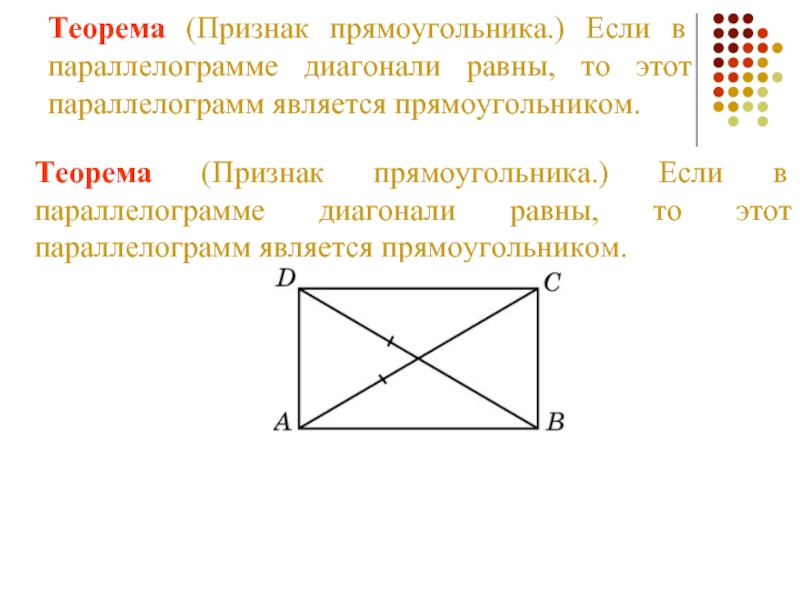
- 8. Теорема (Признак прямоугольника.) Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
- 9. ДАНО:
- 10. Задание Изобразите параллелограмм ABCD, у которого смежные стороны равны, AB=AD. Как называется такой четырехугольник?
- 11. Ромб Параллелограмм, у которого все стороны равны,
- 12. Дано: ABCD- ромб AC∏BD= т.
- 13. III. Закрепление нового материала 1. Меньшая
- 14. Построение. Обозначим сумму двух диагоналей через
- 15. 1. Выучить теорию (п. 31 учебника): определения
Слайд 2I. Устная работа
1) Существует ли параллелограмм, у которого сторона и диагонали
2) Даны два равных и параллельных отрезка. Их концы соединены непересекающимися отрезками. Верно ли, что получившийся четырехугольник является параллелограммом? Почему?
3) Является ли равенство двух противоположных углов четырехугольника признаком параллелограмма?
4) Две стороны четырехугольника параллельны, а две другие равны. Верно ли утверждение о том, что этот четырехугольник является параллелограммом?
5) В параллелограмме один угол прямой. Найдите остальные его углы.
6) Всегда ли параллелограмм является выпуклой фигурой?
Слайд 3II. Новый материал
Изобразим параллелограмм ABCD, у которого все углы прямые.
Вопрос
-
Слайд 5
- Обладает ли прямоугольник всеми свойствами параллелограмма? Почему?
- Перечислите свойства параллелограмма?
-
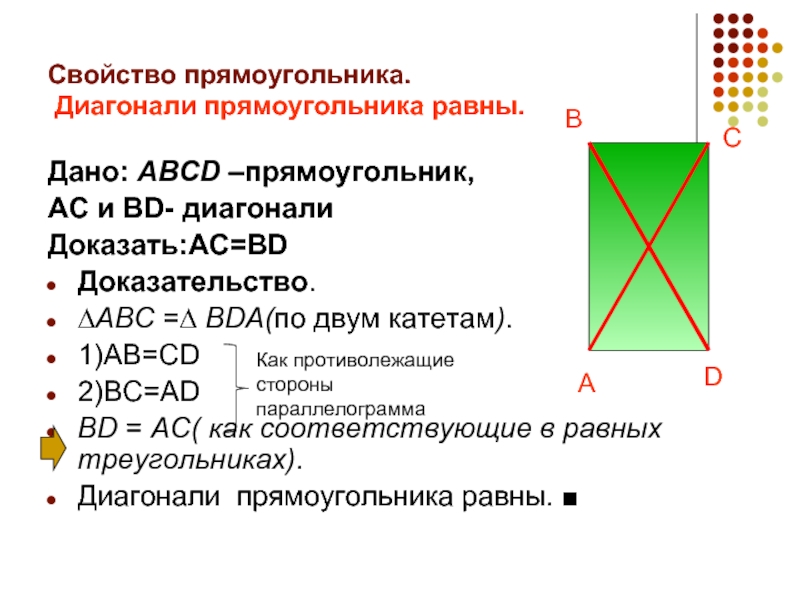
Слайд 6Свойство прямоугольника.
Диагонали прямоугольника равны.
Дано: ABCD –прямоугольник,
AC и BD- диагонали
Доказать:AC=BD
Доказательство.
∆ABC
1)AB=CD
2)BC=AD
BD = AC( как соответствующие в равных треугольниках).
Диагонали прямоугольника равны. ■
Как противолежащие стороны параллелограмма
A
B
C
D
Слайд 7
Задания
- В четырехугольнике ABCD диагонали AC и BD равны. Будет ли
б) прямоугольником?
- В прямоугольнике ABCD диагонали AC и BD равны. Будет ли он прямоугольником?
Слайд 8Теорема (Признак прямоугольника.) Если в параллелограмме диагонали равны, то этот параллелограмм
Слайд 9
ДАНО:
ABCD – параллелограмм
AC=BD
Доказать : ABCD - прямоугольник
Доказательство:
∆ABC =∆
1)AB – общая,
2)AC=BD(по условию),
3)BC=AD
A
B
C
D
(Как противолежащие стороны параллелограмма)
Слайд 10
Задание
Изобразите параллелограмм ABCD, у которого смежные стороны равны, AB=AD. Как называется
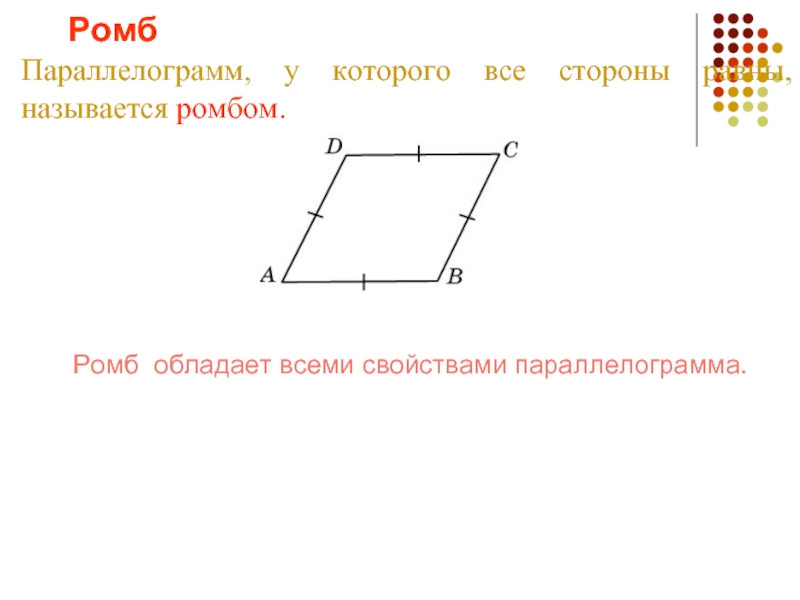
Слайд 11Ромб
Параллелограмм, у которого все стороны равны, называется ромбом.
Ромб обладает
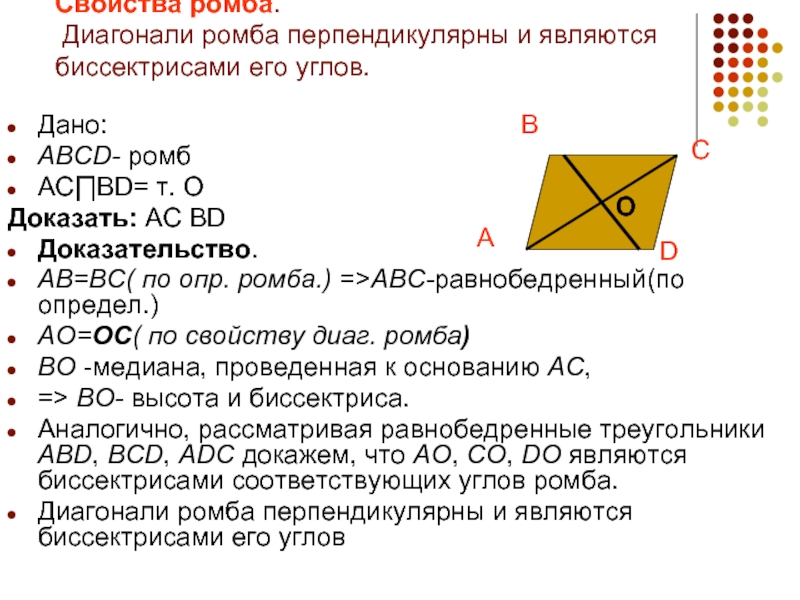
Слайд 12Дано:
ABCD- ромб
AC∏BD= т. О
Доказать: AC BD
Доказательство.
AB=BC( по опр. ромба.)
AO=OC( по свойству диаг. ромба)
BO -медиана, проведенная к основанию AC,
=> BO- высота и биссектриса.
Аналогично, рассматривая равнобедренные треугольники ABD, BCD, ADC докажем, что AO, CO, DO являются биссектрисами соответствующих углов ромба.
Диагонали ромба перпендикулярны и являются биссектрисами его углов
Свойства ромба.
Диагонали ромба перпендикулярны и являются биссектрисами его углов.
A
B
C
D
О
Слайд 13III. Закрепление нового материала
1. Меньшая сторона прямоугольника равна 5 см, диагонали
2. Верно ли утверждение о том, что если в четырехугольнике один угол прямой, а диагонали равны, то он является прямоугольником?
3. Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба.
4*. Постройте прямоугольник по стороне a и сумме диагоналей.
Слайд 14
Построение. Обозначим сумму двух диагоналей через 2d и построим равнобедренный треугольник
Затем продолжим отрезки AO и BO и отложим соответственно равные отрезки OC=AO и OD=BO. ABCD – искомый прямоугольник.
Слайд 151. Выучить теорию (п. 31 учебника): определения прямоугольника и ромба, формулировку
2. Решить задачи.
1)№11
2) №12
3)№17
4*) Постройте прямоугольник по стороне a и сумме другой стороны с диагональю b+d.
IV. Задание на дом