- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проект.Окружность в декартовой системе координат презентация
Содержание
- 1. Проект.Окружность в декартовой системе координат
- 2. Немного о себе. Привет всем! Меня зовут
- 3. Мотивация. Я очень люблю делать презентации. А
- 4. Цель проекта. Рассказать об окружности в Декартовой
- 5. Уравнение окружности Выведем уравнение окружности радиуса
- 6. Пусть точка С имеет координаты
- 7. продолжение Если же точка М (x;y) не
- 8. Задача.№1 Найти уравнение окружности с центром в точке (-3; 4), проходящей через начало координат.
- 9. Задач.№2 Напишите уравнение окружности, проходящей через точки
- 10. Задача.№3 Окружность задана уравнением (x+5) +(y-1) =16.Не
- 11. Интересно и важно Окружностью называется геометрическая фигура,
- 12. продолжение На рисунке 2 отрезки АВ и
- 13. продолжение Центр окружности является серединой любого диаметра.
- 14. продолжение Для изображения окружности на чертеже пользуются
- 16. Пусть Тогда решение последнего уравнения
- 17. Это значит, что прямые не пересекаются, т. е.
- 19. Центр окружности находится в точке с координатами
- 20. Исторический материал Древние египтяне считали площадь круга
- 21. продолжение Хорда разбивает круг на две части,
- 22. Справедливы следующие утверждения: 1. Равные хорды
- 23. Взаимное расположение двух окружностей На рисунке 9,
- 24. продолжение Представьте теперь, что первая окружность передвигается
- 25. Оси симметрии окружности На рисунке 10 изображены
- 26. Теорема Теорема. Окружность симметрична относительно любой прямой,
- 27. Рене Декарт
- 28. Декартова система координат прямолинейная система координат
- 29. продолжение Для задания декартовой прямоугольной системы координат
- 30. Благодарю за внимание!
Слайд 1Проект.
«Окружность в декартовой системе координат»
Над проектом работала Воробьёва
Города Искитима Новосибирской области ,Россия
Руководитель: Кудоспаева Надежда Николаевна.
Слайд 2Немного о себе.
Привет всем!
Меня зовут Алеся
мне 16лет.Живу в Искитиме .Люблю
Слайд 3Мотивация.
Я очень люблю делать презентации. А когда услышала о всероссийском конкурсе,
И ещё я хочу получить хорошую оценку за годовой зачет.
Слайд 4Цель проекта.
Рассказать об окружности в Декартовой системе координат .
Рассказать об окружности.
Рассмотреть
Слайд 5Уравнение окружности
Выведем уравнение окружности радиуса r с центром С в
Слайд 6Пусть точка С имеет
координаты
от произвольной точки М (x;y)
до точки С вычисляется по
формуле МС=
Если точка М лежит на данной окружности, то МС=r ,т.е. координаты точки М удовлетворяют уравнению
Слайд 7продолжение
Если же точка М (x;y) не лежит на данной окружности, то
2
2
2
2
2
2
2
2
Слайд 8Задача.№1
Найти уравнение окружности с центром в точке (-3; 4), проходящей через
Слайд 9Задач.№2
Напишите уравнение окружности, проходящей через точки А(-3;0) и В (0;9), если
Слайд 10Задача.№3
Окружность задана уравнением (x+5) +(y-1) =16.Не пользуясь чертежом, укажите, какие из
А)внутри круга, ограниченного данной окружностью;
Б)на окружности;
В)вне круга, ограниченного данной окружностью.
2
2
Слайд 11Интересно и важно
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных
Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности (рис. 1). Из определения окружности следует, что все радиусы имеют одну и ту же длину. Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.
Слайд 12продолжение
На рисунке 2 отрезки АВ и ЕF — хорды окружности, отрезок
Слайд 13продолжение
Центр окружности является серединой любого диаметра.
Слайд 14продолжение
Для изображения окружности на чертеже пользуются циркулем (рис. 4). Чтобы провести
Слайд 15 Задача
1. Проанализировать взаимное расположение прямых a1x + b1y + c1 = 0, a2x + b2y + c2 = 0.
Решение
Ввиду замечания к доказательству теоремы 11.5 эти уравнения определяют прямые, если a12 + b12 > 0, a22 + b22 > 0.
Пусть для определенности выразим y
из первого уравнения и подставим во
второе: и
или
Слайд 16Пусть Тогда решение последнего уравнения
единственно, и
Таким образом, при условии, что a2b1 – a1b2 ≠ 0, существует единственная точка A(x0; y0), координаты которой удовлетворяют обоим уравнениям, и, следовательно, эти прямые пересекаются в точке А. Пусть теперь
Это значит, если т. е.
то никакое число x не является решением уравнения (*), и, следовательно, исходные уравнения не имеют общих решений.
Слайд 17Это значит, что прямые не пересекаются, т. е. они параллельны. Таким образом,
отношению соответствующих коэффициентов, то уравнения определяют
параллельные прямые. Пусть теперь Тогда любая точка
x – является решением уравнения (*) и в силу произвольности x связь между x и y определяется одним из исходных уравнений, потому что другое уравнение пропорционально первому. В этом случае каждое уравнение совокупности исходных уравнений задает одну и ту же прямую.
Слайд 18
В окружность радиуса R вписан равносторонний треугольник. Доказать, что сумма квадратов расстояний от любой точки окружности до вершин треугольника постоянна, и найти эту сумму.
Решение Шаг 1
Установим координаты вершин треугольника ABC:
B(0; R), Окружность имеет уравнение: x2 + y2 = R2.
Шаг 2
Пусть T – произвольная точка на окружности.
Шаг 3
Согласно формуле расстояния между двумя точками TB2 = x2 + (y- Поэтому Учитывая, что точка T лежит на окружности, имеем: x2 + y2 = R2. Значит, TA2 + TB2 + TC2 = 3R2 + 3R2 = 6R2.
Ответ: 6R2.
2
R)
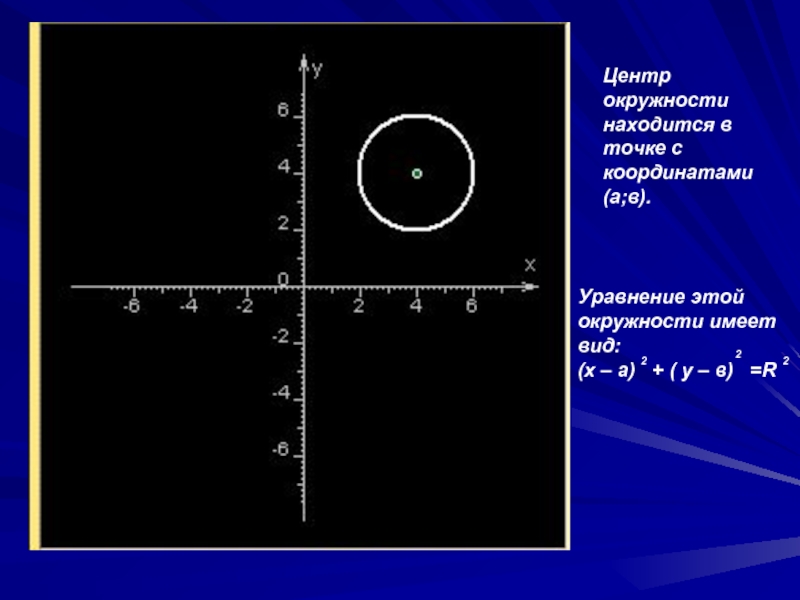
Слайд 19Центр окружности находится в точке с координатами (а;в).
Уравнение этой окружности имеет
2
2
2
Слайд 20Исторический материал
Древние египтяне считали площадь круга равной площади квадрата со стороной
Слайд 21продолжение
Хорда разбивает круг на две части, называемые сегментами (на рис. 7
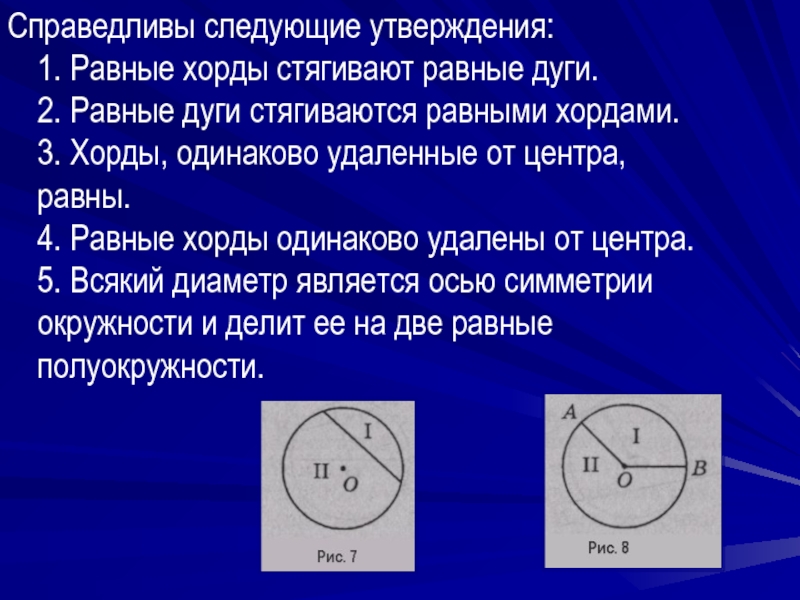
Слайд 22Справедливы следующие утверждения: 1. Равные хорды стягивают равные дуги. 2. Равные
Слайд 23Взаимное расположение двух окружностей
На рисунке 9, а изображены две окружности (О1,r1)
Слайд 24продолжение
Представьте теперь, что первая окружность передвигается так, что расстояние h между
Слайд 25Оси симметрии окружности
На рисунке 10 изображены фигуры (отрезок, окружность, треугольник, квадрат),
Слайд 26Теорема
Теорема. Окружность симметрична относительно любой прямой,
проходящей через ее центр.
Доказательство.
Слайд 28Декартова система координат
прямолинейная система координат на плоскости или в пространстве
Декарт впервые ввел координатную систему, которая существенно отличалась от общепринятой в наши дни. Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета. Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта