Автор:
ученица 9 Б
МОУ СОШ № 7
Струпан Ольга.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проект по теме: Теорема Чевы презентация
Содержание
Слайд 2
Биография ученого
Формулировка теоремы
Доказательство теоремы
Решение задач
Применение теоремы к решение задач
Слайд 3 Биография ученого
Чева
математик. Умер в 1734 г. Главными предметами его занятий были геометрия и механика. Он написал много сочинений. Самым замечательным из них было первое "De lineis rectis se invicem secantibus statica constructio" (Милан, 1678); . В первой его части автор доказывает теорему Менелая и ряд сходных с нею теорем при помощи статического метода, основанного на свойствах центра тяжести системы точек.
Биография подробно.
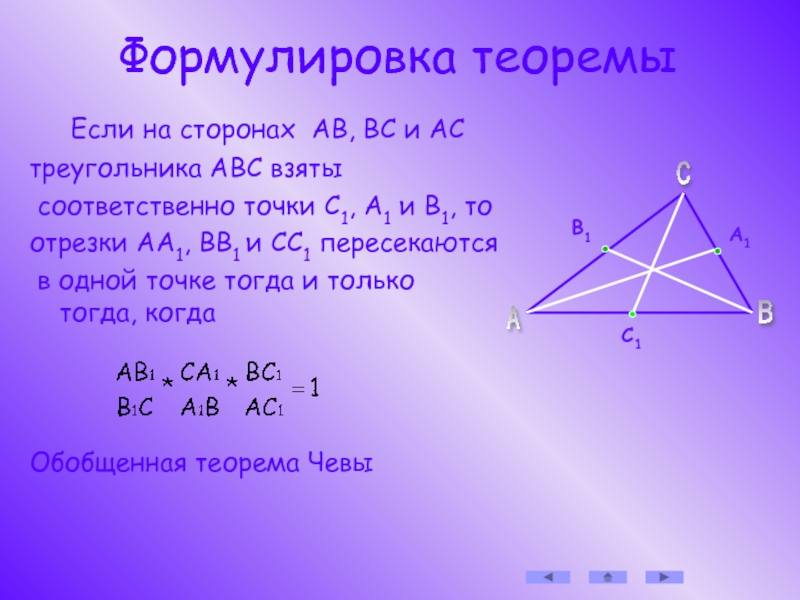
Слайд 4 Формулировка теоремы
Если на сторонах АВ,
треугольника АВС взяты
соответственно точки С1, А1 и В1, то
отрезки АА1, ВВ1 и СС1 пересекаются
в одной точке тогда и только тогда, когда
Обобщенная теорема Чевы
В
С
А
С1
А1
В1
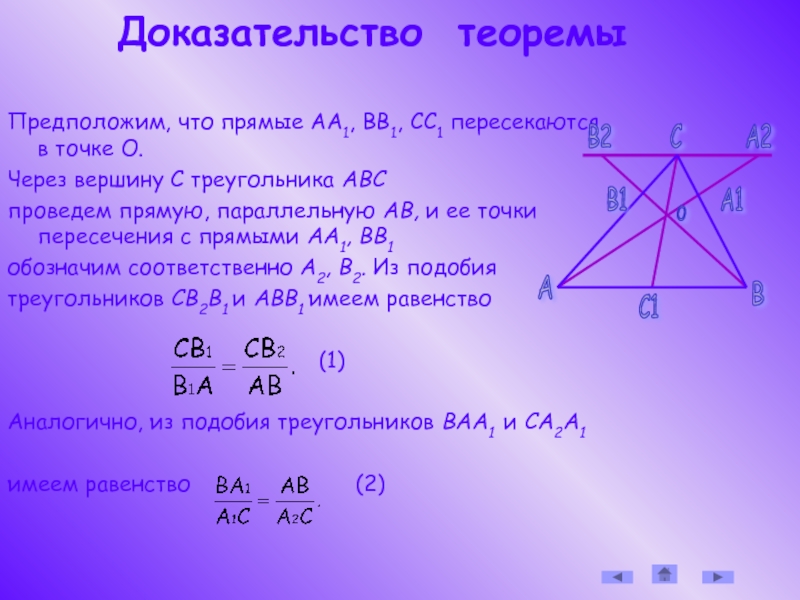
Слайд 5 Доказательство теоремы
Предположим, что прямые АА1, ВВ1, СС1 пересекаются в
Через вершину С треугольника ABC
проведем прямую, параллельную АВ, и ее точки пересечения с прямыми AA1, BB1
обозначим соответственно А2, В2. Из подобия
треугольников СВ2В1 и АВВ1 имеем равенство
(1)
Аналогично, из подобия треугольников ВАА1 и СА2А1
имеем равенство (2)
А
С1
В
А1
А2
С
В2
В1
О
Слайд 6
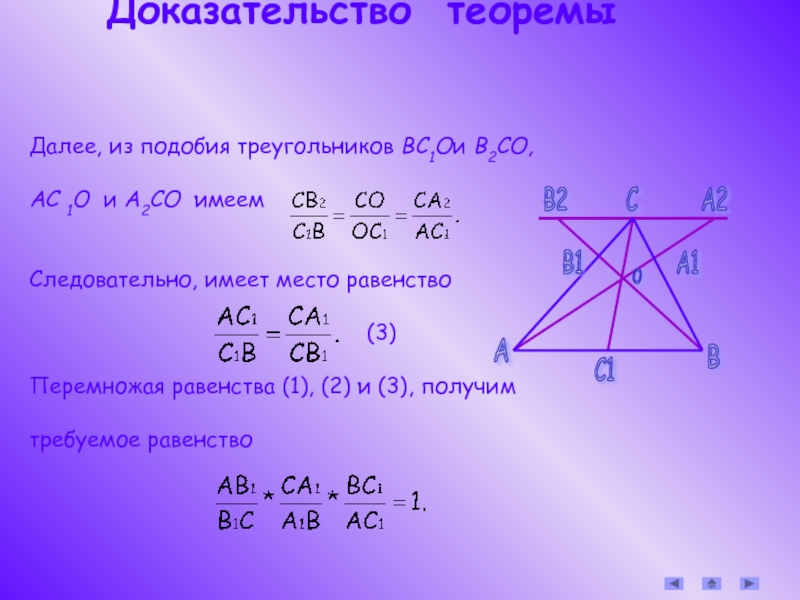
Доказательство теоремы
Далее, из подобия треугольников
AC 1O и А2СО имеем
Следовательно, имеет место равенство
(3)
Перемножая равенства (1), (2) и (3), получим
требуемое равенство
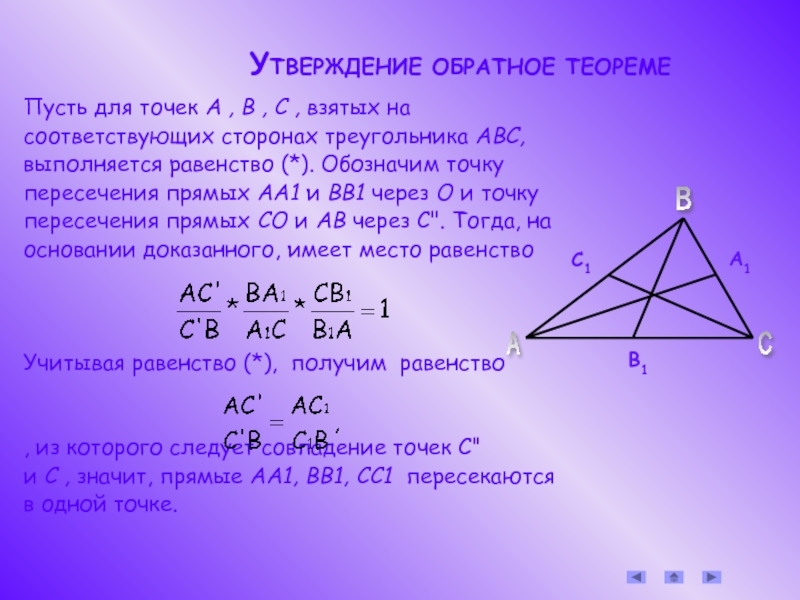
Слайд 7 УТВЕРЖДЕНИЕ ОБРАТНОЕ ТЕОРЕМЕ
Пусть
соответствующих сторонах треугольника ABC,
выполняется равенство (*). Обозначим точку
пересечения прямых АА1 и ВВ1 через О и точку
пересечения прямых СО и АВ через С". Тогда, на
основании доказанного, имеет место равенство
Учитывая равенство (*), получим равенство
, из которого следует совпадение точек С"
и С , значит, прямые АА1, BB1, СС1 пересекаются
в одной точке.
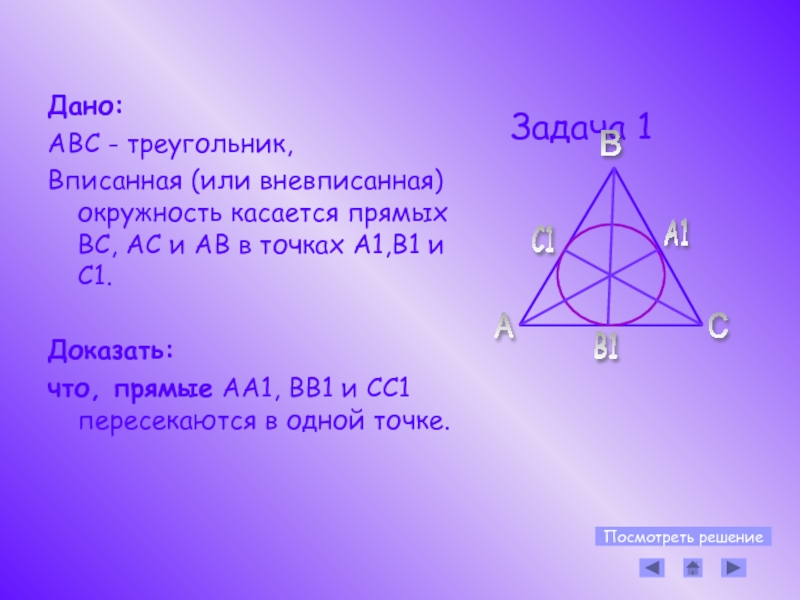
Слайд 9
Дано:
АВС - треугольник,
Вписанная (или вневписанная) окружность касается прямых ВС, АС и АВ в точках А1,В1 и С1.
Доказать:
что, прямые AA1, BB1 и CC1 пересекаются в одной точке.
Посмотреть решение
Слайд 10
Ясно, что АВ1=АС1, ВС1 =ВА1,
и СА1 = СВ1, причем в случае
вписанной окружности на
сторонах треугольника АВС
лежат три точки, а в случае
вневписанной – одна точка.
Воспользовавшись теоремой Чевы, получим что прямые AA1, BB1 и CC1 пересекаются в одной точке.
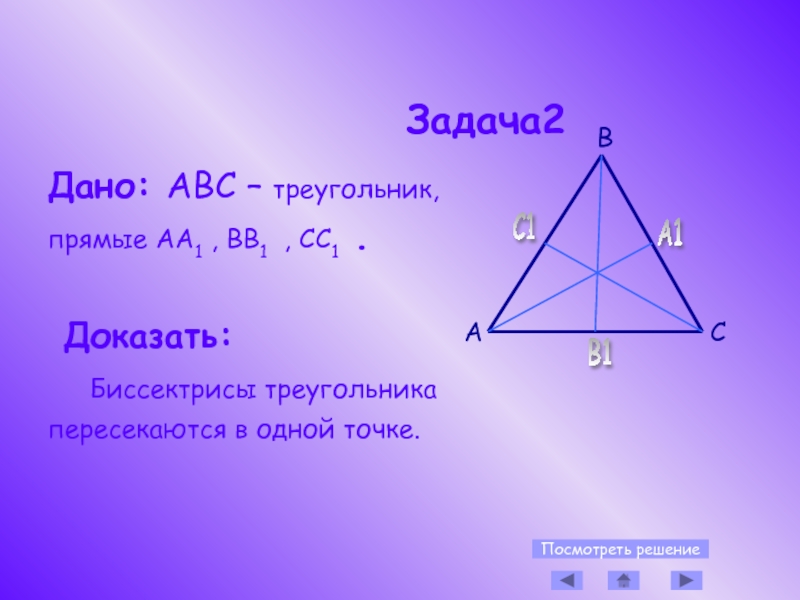
Слайд 11
Дано: АВС – треугольник,
прямые АА1 , ВВ1 , СС1 .
Доказать:
Биссектрисы треугольника
пересекаются в одной точке.
С
В
А
А1
В1
С1
Посмотреть решение
Слайд 12 Доказательство:
пусть АА1 ,ВВ1
треугольника АВС. Тогда
Следовательно
значит, АА1,ВВ1, СС1 пересекаются в одной точке.
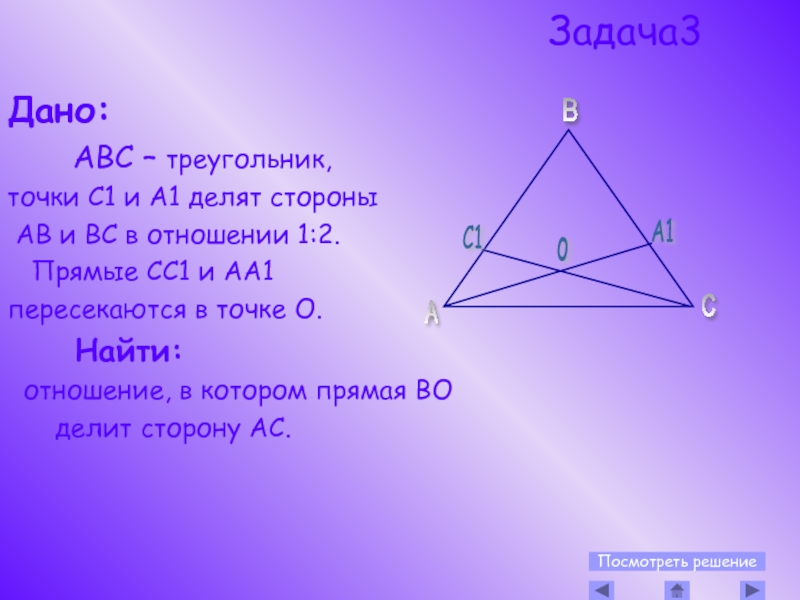
Слайд 13
Дано:
АВС – треугольник,
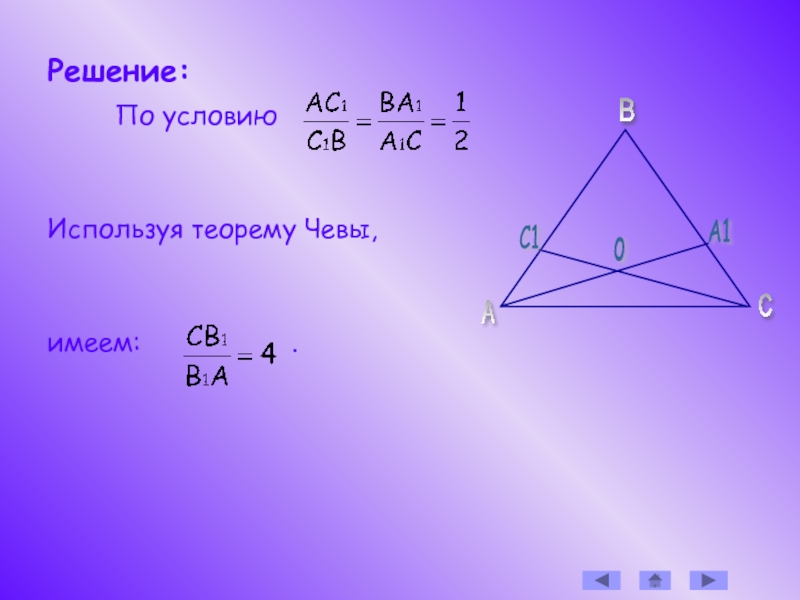
точки С1 и А1 делят стороны
АВ и ВС в отношении 1:2.
Прямые СС1 и АА1
пересекаются в точке О.
Найти:
отношение, в котором прямая ВО
делит сторону АС.
Посмотреть решение
Слайд 15
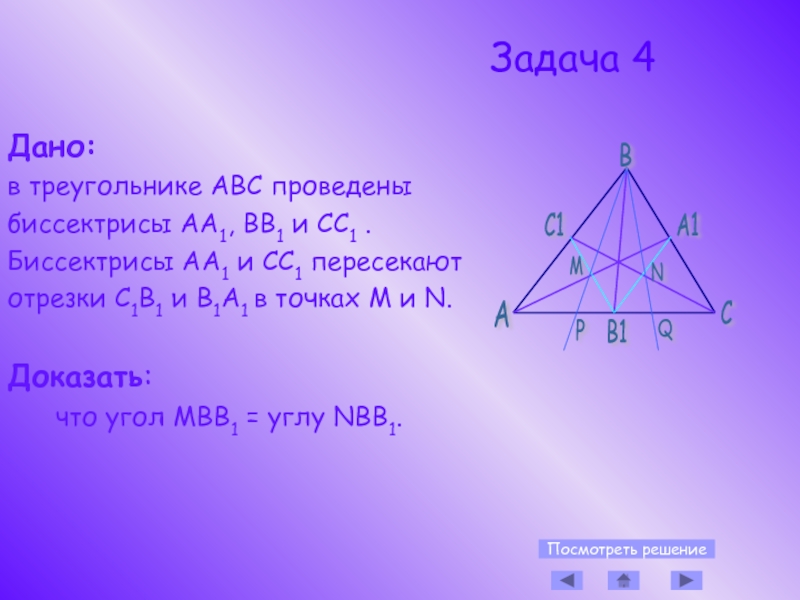
Дано:
в треугольнике АВС проведены
биссектрисы АА1, ВВ1 и СС1 .
Биссектрисы АА1 и СС1 пересекают
отрезки С1В1 и В1А1 в точках M и N.
Доказать:
что угол MBB1 = углу NBB1.
Посмотреть решение
Слайд 16
Пусть отрезки ВМ и ВН пересекают сторону АС в точках Р и Q. тогда(1)
если О- точка пересечения биссектрис треугольника АВС, то (2)
,а значит,(3).
Заметив, что ВС1:С1А=ВС:СА , и
проведя аналогичные вычисления для sin QBB1:sin QBC,получим
sinPBB1:sinPBA=sinQBB1:sin QBC.
так как угол авв1=угол свв1,
то угол рвв1=угол qbb1.
Слайд 17Применение теоремы
Полезна она вот почему: те задачи, которые
традиционно решаются довольно сложно с помощью
аппарата векторной алгебры, решаются буквально в
одну строчку с помощью теоремы Чевы. Это касается
и обратной теоремы. Доказательство того, что три
прямые пересекаются в одной точке, так же легко
решается с помощью теоремы, обратной теореме
Чевы. Я считаю, что это одно из наиболее важных
событий в истории геометрии (открытие этой
теоремы), оказавшее влияние как на процесс развития
математики, так и на развитие техники и смежных
областей науки!