ЛЕНЬШИНА АЛИНА 9 «А»
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРЕЗЕНТАЦИЯ НА ТЕМУ РАВЕНСТВО ТРЕУГОЛЬНИКОВ презентация
Содержание
- 1. ПРЕЗЕНТАЦИЯ НА ТЕМУ РАВЕНСТВО ТРЕУГОЛЬНИКОВ
- 3. - геометрическая фигура, состоит из 3х точек
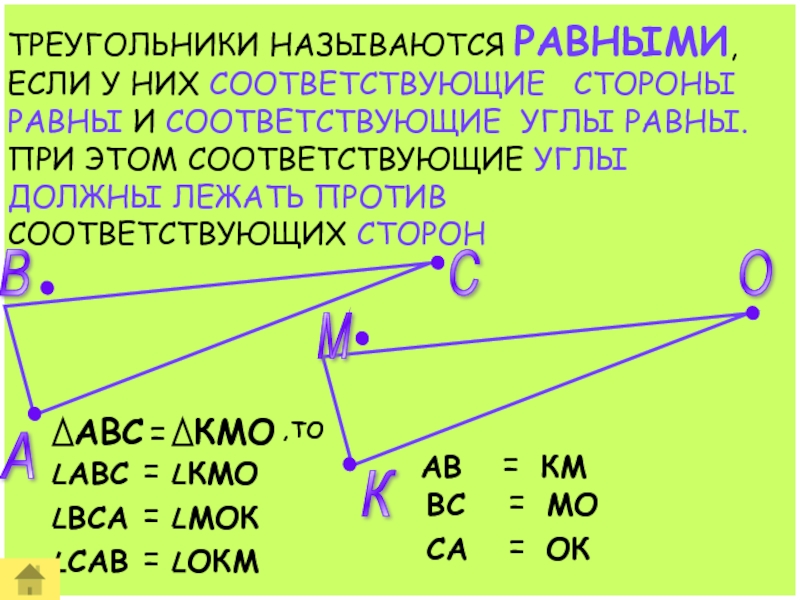
- 4. ТРЕУГОЛЬНИКИ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ У НИХ
- 7. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (ПРИЗНАК ПО СТОРОНАМ
- 8. С А В ДОКАЗАТЕЛЬСТВО: ДАНО:
- 10. ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (ПРИЗНАК ПО СТОРОНЕ
- 11. ДАНО: АВС и А1В1С1 АB=А1B1 LА=LА1 L
- 13. ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (ПРИЗНАК ПО
- 14. ДАНО: АВС и А1В1С1 АB=А1B1 BC=B1C1 CА=C1А1
- 17. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ 1*.
- 18. 4. В треугольниках МРК и АОВ сторона
- 19. 6. Закончите предложение: «Первый признак равенства треугольников
- 20. 7. У треугольников АВС и А1В1С1 равны
- 21. 8. Докажите равенство треугольников АВС и СМК [ ВМК ].
- 23. ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ 1*. В
- 24. 3. В треугольниках KNM и PQT [ABC
- 25. 5. В треугольниках BCD и MPQ [MPQ
- 26. 7. У треугольников АВС и А1В1С1 равны
- 27. 9. Докажите равенство треугольников АВС и СМК [ ВМК ].
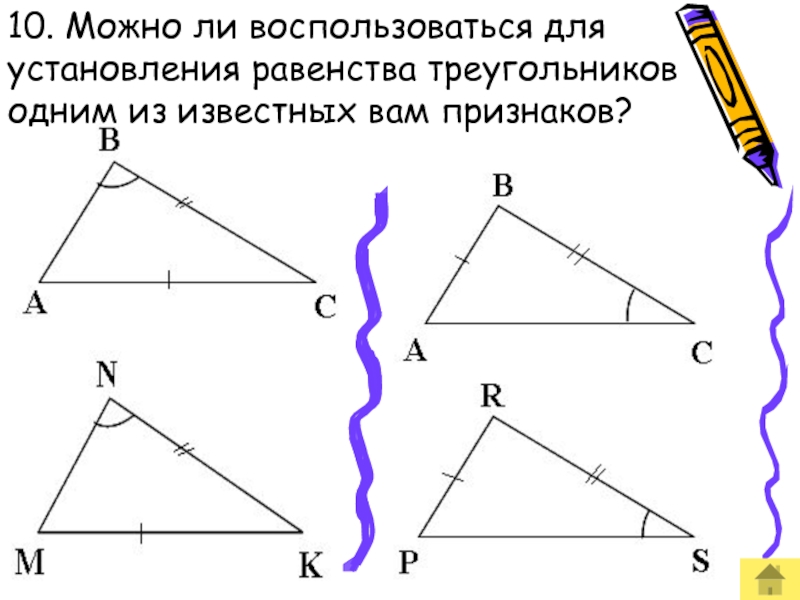
- 28. 10. Можно ли воспользоваться для установления равенства треугольников одним из известных вам признаков?
- 30. ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ 1.
- 31. 3. Сколько равных пар сторон надо найти,
- 32. 5. Закончите предложение: «Третий признак равенства
- 33. 7. Докажите равенство треугольников АВС и АСМ [ АМК и АВК ].
- 34. 8. Докажите равенство треугольников АВС и АМК [ ЕСМ и КСМ ].
- 35. 9. Докажите равенство треугольников СОВ и СМО [ОМА и ОРС].
- 37. Равенство треугольников. Медиана, высота и биссектриса треугольника. Вариант 1 Вариант 2
- 38. Равенство треугольников. Медиана, высота и биссектриса
- 39. Какое из высказываний верное? 3. Дано:
- 40. 5. В треугольник МРК и BDE проведены
- 41. 7. Сколько пар равных треугольников на рисунке?
- 42. Равенство треугольников. Медиана, высота и биссектриса треугольника. Вариант 1 Вариант 2
- 43. Вариант 2 1. Известно ,что AO
- 44. 2. OH и ON – высоты углов
- 45. 3. Дано: ABC = DEF,
- 46. 5. В треугольник ABC и KPM проведены
- 47. 7. Сколько пар равных треугольников на рисунке?
- 48. ПРОВЕРЬ СЕБЯ!
- 50. КОНТРОЛЬНЫЕ РАБОТЫ
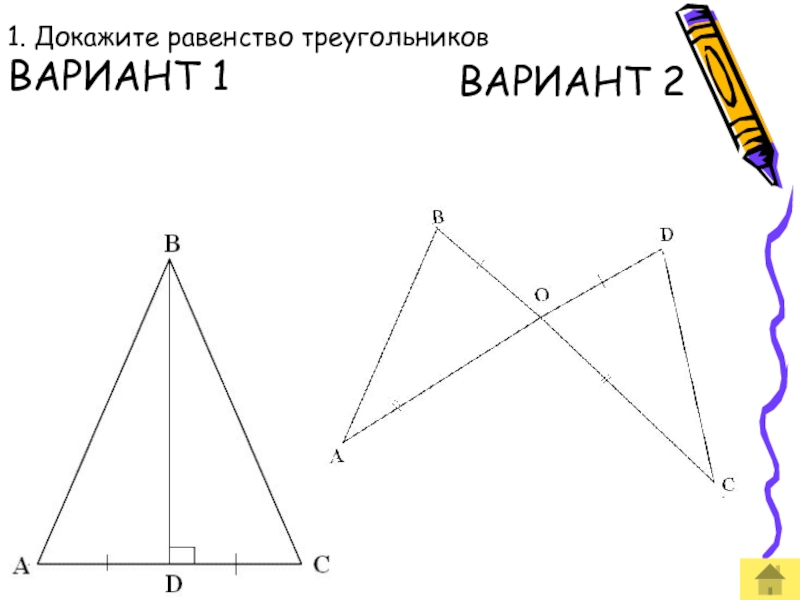
- 51. 1. Докажите равенство треугольников ВАРИАНТ 1 ВАРИАНТ 2
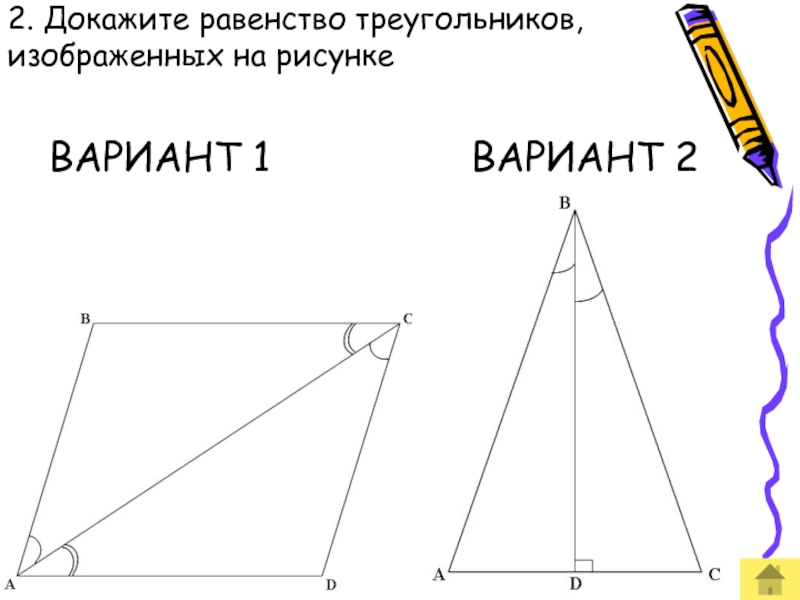
- 52. 2. Докажите равенство треугольников, изображенных на рисунке ВАРИАНТ 1 ВАРИАНТ 2
- 53. КОНТРОЛЬНЫЕ РАБОТЫ
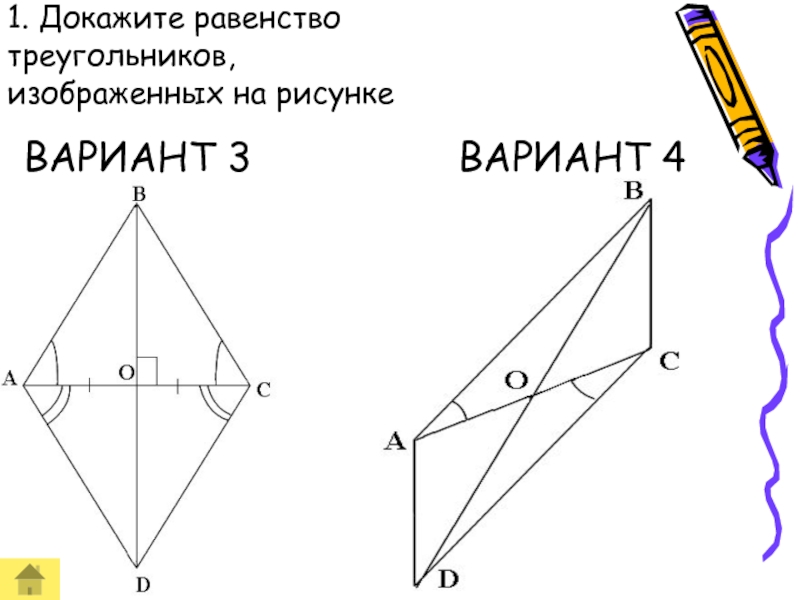
- 54. ВАРИАНТ 3 1. Докажите равенство треугольников, изображенных на рисунке ВАРИАНТ 4
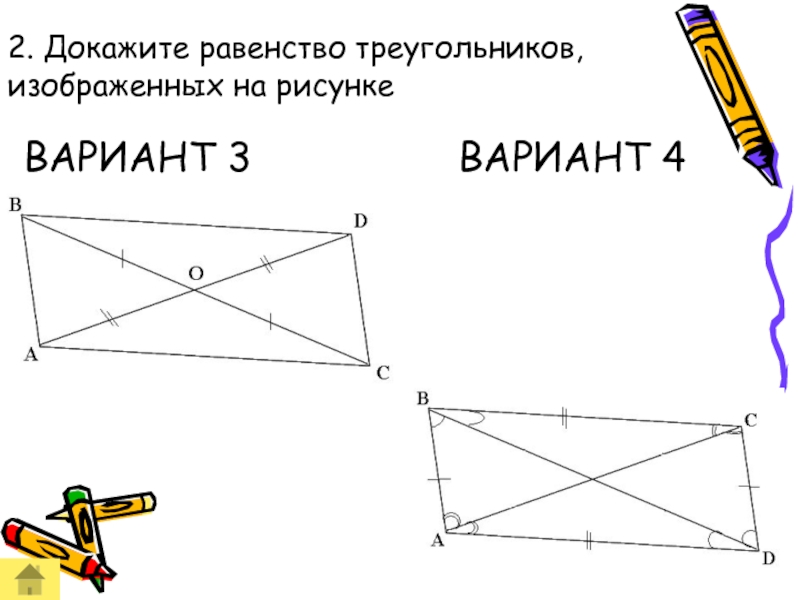
- 55. 2. Докажите равенство треугольников, изображенных на рисунке ВАРИАНТ 3 ВАРИАНТ 4
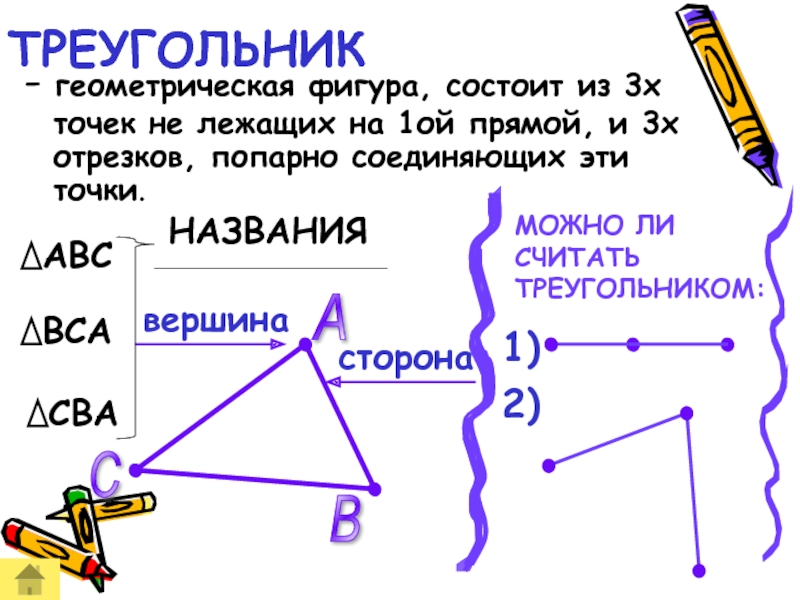
Слайд 3- геометрическая фигура, состоит из 3х точек не лежащих на 1ой
прямой, и 3х отрезков, попарно соединяющих эти точки.
вершина
сторона
А
В
С
НАЗВАНИЯ
МОЖНО ЛИ СЧИТАТЬ ТРЕУГОЛЬНИКОМ:
ТРЕУГОЛЬНИК
Слайд 4
ТРЕУГОЛЬНИКИ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ У НИХ СООТВЕТСТВУЮЩИЕ СТОРОНЫ РАВНЫ И
СООТВЕТСТВУЮЩИЕ УГЛЫ РАВНЫ. ПРИ ЭТОМ СООТВЕТСТВУЮЩИЕ УГЛЫ ДОЛЖНЫ ЛЕЖАТЬ ПРОТИВ СООТВЕТСТВУЮЩИХ СТОРОН
А
В
С
М
К
О
Слайд 7ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
(ПРИЗНАК ПО СТОРОНАМ
И УГЛУ МЕЖДУ НИМИ)
ЕСЛИ ДВЕ
СТОРОНЫ И УГОЛ МЕЖДУ НИМИ ОДНОГО ТРЕУГОЛЬНИКА РАВНЫ СООТВЕТСТВЕННО ДВУМ СТОРОНАМ И УГЛУ МЕЖДУ НИМИ ДРУГОГО ТРЕУГОЛЬНИКА, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ
Слайд 8
С
А
В
ДОКАЗАТЕЛЬСТВО:
ДАНО:
АВС и
А1В1С1
АВ=А1В1
АС=А1С1
LА=LА1
ДОКАЗАТЬ:
АВС=
А1В1С1
С1
А1
В1
1.
ДОКАЖЕМ,ЧТО ТРЕУГОЛЬНИКИ РАВНЫ
2.
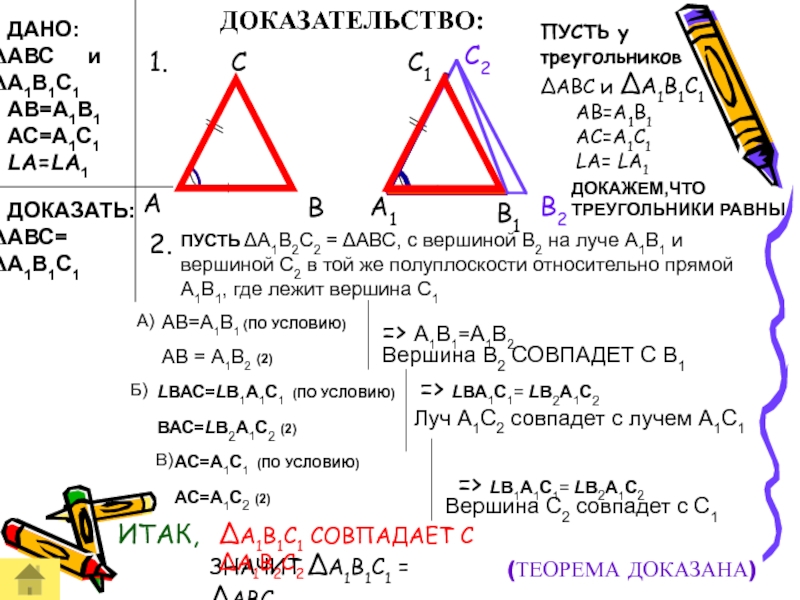
ПУСТЬ у треугольников ΔАВС и ΔА1В1С1
АВ=А1В1
АС=А1С1
LА= LА1
АС=А1С1
LА= LА1
ПУСТЬ ΔА1В2С2 = ΔАВС, с вершиной В2 на луче А1В1 и вершиной С2 в той же полуплоскости относительно прямой А1В1, где лежит вершина С1
=> А1В1=А1В2
АВ=А1В1 (ПО УСЛОВИЮ)
АВ = А1В2 (2)
Вершина В2 СОВПАДЕТ С В1
А)
=> LВА1С1= LВ2А1С2
Луч А1С2 совпадет с лучем А1С1
LВАС=LВ1А1С1 (ПО УСЛОВИЮ)
ВАС=LВ2А1С2 (2)
Б)
АС=А1С1 (ПО УСЛОВИЮ)
АС=А1С2 (2)
=> LВ1А1С1= LВ2А1С2
Вершина С2 совпадет с С1
В)
ЗНАЧИТ ΔА1В1С1 = ΔАВС.
В2
С2
ИТАК,
ΔА1В1С1 СОВПАДАЕТ С ΔА1В2С2
(ТЕОРЕМА ДОКАЗАНА)
Слайд 10ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
(ПРИЗНАК ПО СТОРОНЕ
И ПРИЛЕЖАЩИМ К НЕЙ УГЛАМ)
ЕСЛИ
СТОРОНА И ПРИЛЕЖАЩИЕ К НЕЙ УГЛЫОДНОГО ТРЕУГОЛЬНИКА РАВНЫ СООТВЕТСТВЕННО СТОРОНЕ И ПРИЛЕЖАЩИМ К НЕЙ УГЛАМ ДРУГОГО ТРЕУГОЛЬНИКА, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ.
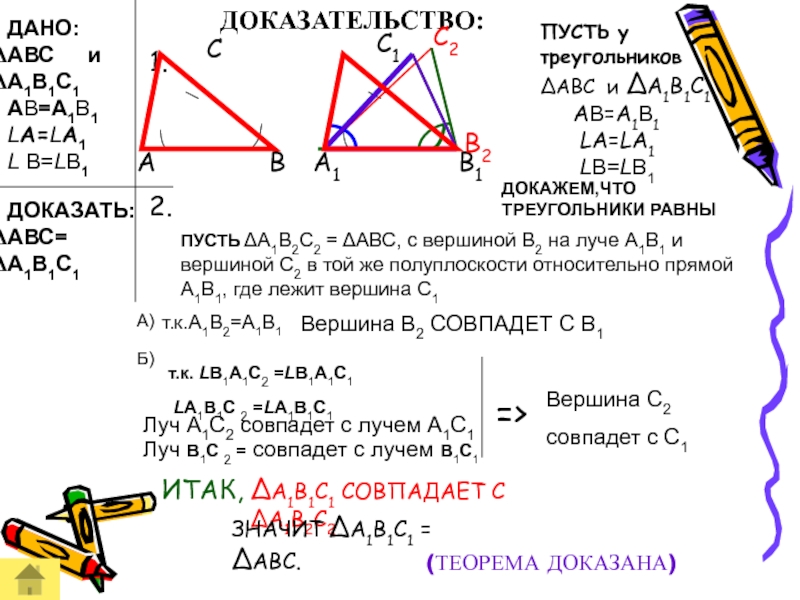
Слайд 11ДАНО:
АВС и
А1В1С1
АB=А1B1
LА=LА1
L B=LB1
ДОКАЗАТЬ:
АВС=
А1В1С1
ДОКАЗАТЕЛЬСТВО:
1.
С
А
В
С1
А1
В1
ПУСТЬ у треугольников ΔАВС и ΔА1В1С1
АB=А1B1
LА=LА1
LB=LB1
LА=LА1
LB=LB1
ДОКАЖЕМ,ЧТО ТРЕУГОЛЬНИКИ РАВНЫ
2.
ПУСТЬ ΔА1В2С2 = ΔАВС, с вершиной В2 на луче А1В1 и вершиной С2 в той же полуплоскости относительно прямой А1В1, где лежит вершина С1
А)
т.к.А1В2=А1В1
Вершина В2 СОВПАДЕТ С В1
Б)
т.к. LВ1А1С2 =LВ1А1С1
LА1В1С 2 =LА1В1С1
Луч А1С2 совпадет с лучем А1С1
Луч В1С 2 = совпадет с лучем В1С1
Вершина С2
совпадет с С1
=>
ИТАК,
ΔА1В1С1 СОВПАДАЕТ С ΔА1В2С2
ЗНАЧИТ ΔА1В1С1 = ΔАВС.
(ТЕОРЕМА ДОКАЗАНА)
В2
С2
Слайд 13ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
(ПРИЗНАК ПО ТРЕМ СТОРОНАМ )
ЕСЛИ ТРИ СТОРОНЫ ОДНОГО
ТРЕУГОЛЬНИКА РАВНЫ СООТВЕТСТВЕННО ТРЕМ СТОРОНАМ ДРУГОГО ТРЕУГОЛЬНИКА, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ.
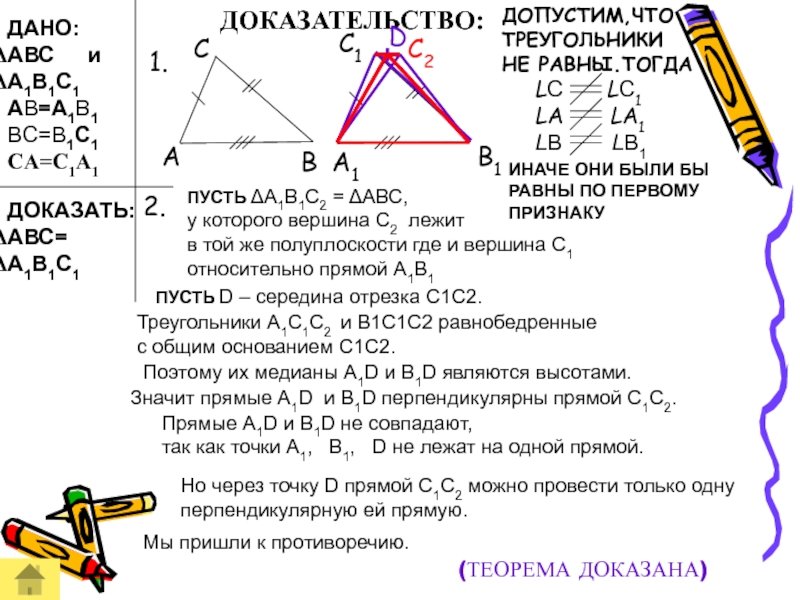
Слайд 14ДАНО:
АВС и
А1В1С1
АB=А1B1
BC=B1C1
CА=C1А1
ДОКАЗАТЬ:
АВС=
А1В1С1
2.
ДОКАЗАТЕЛЬСТВО:
1.
С
А
В
С1
А1
В1
ПУСТЬ ΔА1В1С2 = ΔАВС,
у которого вершина С2 лежит
в той
же полуплоскости где и вершина С1
относительно прямой А1В1
ДОПУСТИМ,ЧТО ТРЕУГОЛЬНИКИ
НЕ РАВНЫ.ТОГДА
LС LС1
LА LА1
LB LB1
ИНАЧЕ ОНИ БЫЛИ БЫ РАВНЫ ПО ПЕРВОМУ ПРИЗНАКУ
С2
Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую.
ПУСТЬ D – середина отрезка С1С2.
D
Треугольники А1С1С2 и В1С1С2 равнобедренные
с общим основанием С1С2.
Поэтому их медианы А1D и В1D являются высотами.
Значит прямые А1D и В1D перпендикулярны прямой С1С2.
Прямые А1D и В1D не совпадают,
так как точки А1, В1, D не лежат на одной прямой.
Мы пришли к противоречию.
(ТЕОРЕМА ДОКАЗАНА)
Слайд 17ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
1*. В треугольниках ABC и DEF [ABD
и MPQ]
сторона AB [AD] равна DE [MQ], сторона BC [BD]
равна EF [PQ], угол C [D] равен углу F [Q].
Можно ли на основании первого признака равенства утверждать, что эти треугольники равны?
2*. В треугольниках KLM и FPQ [ABC и KLM] сторона KL [AB] равна FP [KL], сторона KM [BC] равна FQ [LM],
угол K [A] равен углу F [K]. Можно ли на основании первого признака равенства утверждать, что эти треугольники равны?
Слайд 184. В треугольниках МРК и АОВ сторона МР равна АО, сторона
МК равна АВ. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными
по первому признаку?
[Закончите предложение:
«Первый признак равенства треугольников – это признак равенства по…» ]
3 . В треугольниках KNO и PQT [ABC и DEF]
равные стороны KN [AB] и PQ [DE] и
углы K[A] и P [D]. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались
равными по первому признаку?
Слайд 196. Закончите предложение: «Первый признак равенства треугольников – это признак равенства
по…»
[ В треугольниках PQR и CST сторона PR равна CT, сторона QR равна ST.
Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по первому признаку? ]
5. В треугольниках АВС и DEF стороны АВ и ВС
[MPQ и KLT стороны MP и PQ] равны соответственно сторонам DE и EF [KL и LT]. Треугольники эти
не равны.
Что можно сказать об углах В и Е[ P и L]?
Слайд 207. У треугольников АВС и А1В1С1 равны стороны АС и А1С1
и углы А и А1.
Равенство каких сторон или углов надо установить,
чтобы сделать вывод о равенстве треугольников на основании первого признака равенства?
[У треугольников АВС и А1В1С1 равны стороны ВС и В1С1 и углы С и С1.
Равенство каких сторон или углов надо установить, чтобы сделать вывод о равенстве треугольников на основании первого признака равенства треугольников? ]
Слайд 23ВТОРОЙ ПРИЗНАК РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
1*. В треугольниках АВС и DEF [ABC и
MNQ]
сторона AB равна DE [MP], углы A и B равны соответственно углам D и F [M и P].
Равны ли эти треугольники по второму признаку треугольников?
2. В треугольниках KMN и PQT [ABC и KLM]
сторона NM [AB] и N [A] и M [B] равны соответственно стороне PQ [KL] и углам P [K] и Q[M].
Равны ли эти треугольники по второму признаку?
Слайд 243. В треугольниках KNM и PQT [ABC и DEF] сторона [углы]
KN [A и C] равна [равны] стороне PQ [соответственно углам D и F ].
Угол N = углу Q. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались
равными по второму признаку?
4. В треугольниках MQP и LKT [BCD и MPK] углы [сторона] M и Q [CD] равны [равна] соответственно углам [стороне] L и T [PK,угол D= углу K]. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по второму признаку?
4. В треугольниках MQP и LKT [BCD и MPK] углы [сторона] M и Q [CD] равны [равна] соответственно углам [стороне] L и T [PK,угол D= углу K]. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по второму признаку?
Слайд 255. В треугольниках BCD и MPQ [MPQ и KLT] углы B
[M] и D [Q] равны соответственно
углам M [K] и Q [T] .
Треугольники эти не равны.
Что от сюда следует в соответствии со вторым
признаком треугольников?
6. Закончите предложение: «Второй признак равенства треугольников – это признак равенства по…» [сколько условий должно выполняться, чтобы треугольники CDE и XYZ оказались равными по определению равных треугольников; сколько – для равенства по первому признаку; сколько - для равенства по второму признаку?]
6. Закончите предложение: «Второй признак равенства треугольников – это признак равенства по…» [сколько условий должно выполняться, чтобы треугольники CDE и XYZ оказались равными по определению равных треугольников; сколько – для равенства по первому признаку; сколько - для равенства по второму признаку?]
Слайд 267. У треугольников АВС и А1В1С1 равны стороны ВС и В1С1
и углы С и С1. Равенство каких
еще сторон или углов надо установить,
чтобы сделать вывод о равенстве треугольников на основании второго признака равенства?
[У треугольников АВС и А1В1С1 равны стороны АС и А1С1 и углы А и А1. равенство каких сторон или углов надо установить, чтобы сделать вывод о равенстве
треугольников на основании второго признака равенства треугольников?]
8. Сколько условий должно выполниться, чтобы треугольники АВС и MPQ оказались равными по определению равных треугольников; сколько – для равенства по первому признаку; сколько - для равенства по второму признаку? [Закончите предложение: «Второй признак равенства треугольников – это признак равенства по…»]
8. Сколько условий должно выполниться, чтобы треугольники АВС и MPQ оказались равными по определению равных треугольников; сколько – для равенства по первому признаку; сколько - для равенства по второму признаку? [Закончите предложение: «Второй признак равенства треугольников – это признак равенства по…»]
Слайд 2810. Можно ли воспользоваться для установления равенства треугольников одним из известных
вам признаков?
Слайд 30ТРЕТИЙ ПРИЗНАК РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
1. Стороны одного треугольника равны 30см, 40см
и 0,5м, а другого – 30см, 40см и 5дм.
Равны ли эти треугольники? [ В треугольнике АВС стороны 20см, 30см и 0,4дм, а в треугольнике ЕМК стороны равны 20см, 30см и 0,4м. Равны ли эти треугольники?]
Равны ли эти треугольники? [ В треугольнике АВС стороны 20см, 30см и 0,4дм, а в треугольнике ЕМК стороны равны 20см, 30см и 0,4м. Равны ли эти треугольники?]
2. В треугольниках ВОС и МАЕ равны стороны ВО и МА,
ОС и АЕ.[В треугольниках АСМ и ВЕК стороны
АС и СМ равны соответственно сторонам ВЕ и ЕК.] Обязательно ли эти треугольники равны?
Слайд 313. Сколько равных пар сторон надо найти, доказывая равенство двух треугольников:
А)
по определению
Б) по первому признаку
В) по второму признаку
Г) по третьему признаку
[ Закончите предложение:
«третий признак равенства треугольников – это признак равенства по …».]
Б) по первому признаку
В) по второму признаку
Г) по третьему признаку
[ Закончите предложение:
«третий признак равенства треугольников – это признак равенства по …».]
4. В треугольниках АВС и PОT [МКE] стороны АВ и ВC равны соответственно сторонам РО и ОТ [MK и KE].
Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными
по третьему признаку?
Слайд 325. Закончите предложение: «Третий признак равенства треугольников – это признак равенства
по…»
[сколько пар равных углов надо найти,
доказывая равенство двух треугольников:
А) по первому признаку
Б) по второму признаку
В) по третьему признаку?
А) по первому признаку
Б) по второму признаку
В) по третьему признаку?
6. В неравных треугольниках АВС и МЕК стороны
АВ и ВС равны соответственно сторонам МЕ и ЕК.
Может ли сторона АС быть равной стороне МК?
[Стороны треугольника ВСМ равны 6см, 8см и 10см,
а две стороны треугольника КОА равны 10см и 6см.
Что можно сказать о третей стороне этого треугольника, если известно, что
треугольники не равны? ]
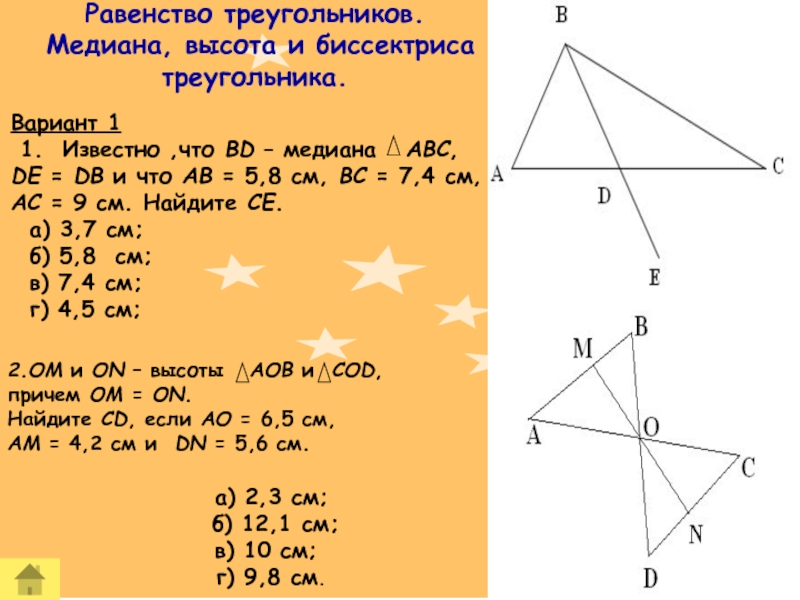
Слайд 38Равенство треугольников.
Медиана, высота и биссектриса
треугольника.
Равенство треугольников.
Медиана, высота и
биссектриса
треугольника.
треугольника.
Вариант 1
1. Известно ,что BD – медиана ABC,
DE = DB и что AB = 5,8 см, BC = 7,4 см, AC = 9 см. Найдите CE.
а) 3,7 см;
б) 5,8 см;
в) 7,4 см;
г) 4,5 см;
2.OM и ON – высоты AOB и COD,
причем OM = ON.
Найдите CD, если AO = 6,5 см,
AM = 4,2 см и DN = 5,6 см.
а) 2,3 см;
б) 12,1 см;
в) 10 см;
г) 9,8 см.
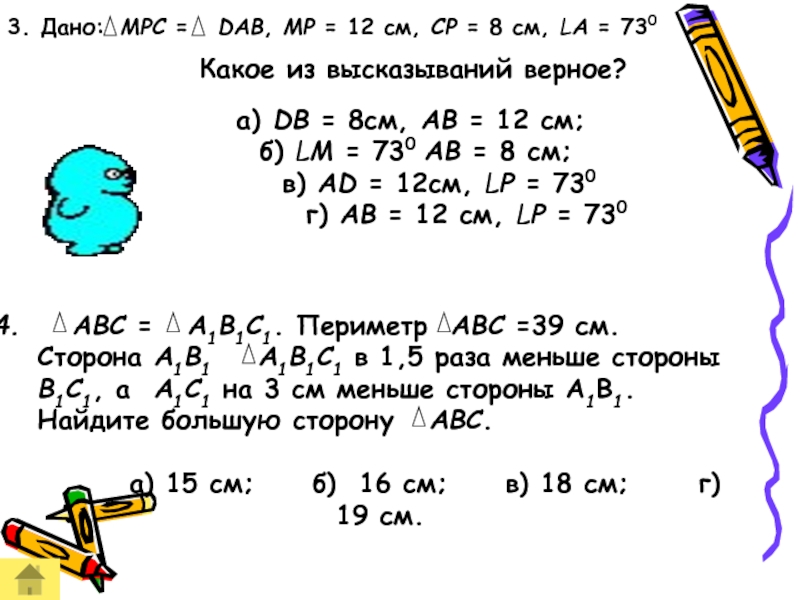
Слайд 39Какое из высказываний верное?
3. Дано:
MPC = DAB, MP
= 12 см, CP = 8 см, LA = 730
а) DB = 8см, АВ = 12 см;
б) LM = 730 АВ = 8 см;
в) AD = 12см, LP = 730
г) AB = 12 см, LP = 730
АВС = А1В1С1. Периметр АВС =39 см. Сторона А1В1 А1В1С1 в 1,5 раза меньше стороны В1С1, а А1С1 на 3 см меньше стороны А1В1. Найдите большую сторону АВС.
а) 15 см; б) 16 см; в) 18 см; г) 19 см.
Слайд 405. В треугольник МРК и BDE проведены две биссектрисы РС и
DN; треугольник МРС равен треугольнику BDN. Найдите отрезок NE, если МК =8см, а BN < NE на 2,4 см.
а) 2,8 см; б) 5,2 см; в) 5,6 см; г) 2,6см.
а) 2,8 см; б) 5,2 см; в) 5,6 см; г) 2,6см.
6. прямая АВ разбивает плоскость на две полуплоскости. Из точек А и В в разные полуплоскости проведены равные отрезки AD и BC, причем угол BAD равен углу ABC.
Какие из высказываний верные:
1) CAD = BDA; 3) BAD = BAC;
2) LDBA = LCAB; 4) ADB = BCA?
а) 2;4; б) 2;3;4; в) 1;4; г) 1;2;3;4.
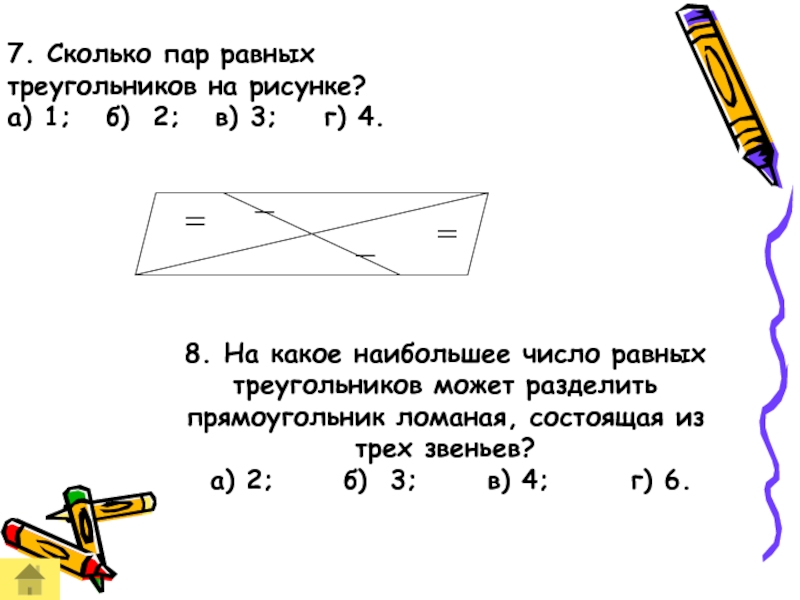
Слайд 417. Сколько пар равных треугольников на рисунке?
а) 1; б)
2; в) 3; г) 4.
8. На какое наибольшее число равных треугольников может разделить прямоугольник ломаная, состоящая из трех звеньев?
а) 2; б) 3; в) 4; г) 6.
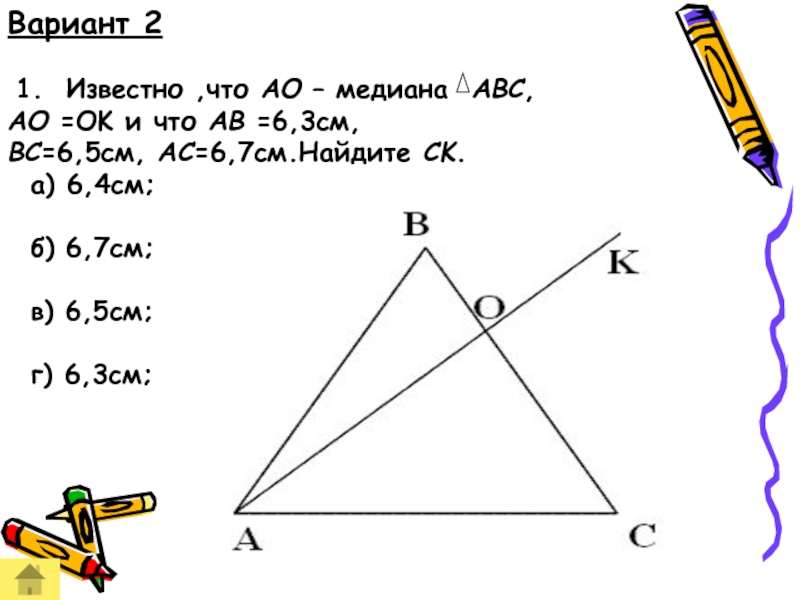
Слайд 43Вариант 2
1. Известно ,что AO – медиана ABC,
AO =OK и
что AB =6,3см,
BC=6,5см, AC=6,7см.Найдите CK.
а) 6,4см;
б) 6,7см;
в) 6,5см;
г) 6,3см;
BC=6,5см, AC=6,7см.Найдите CK.
а) 6,4см;
б) 6,7см;
в) 6,5см;
г) 6,3см;
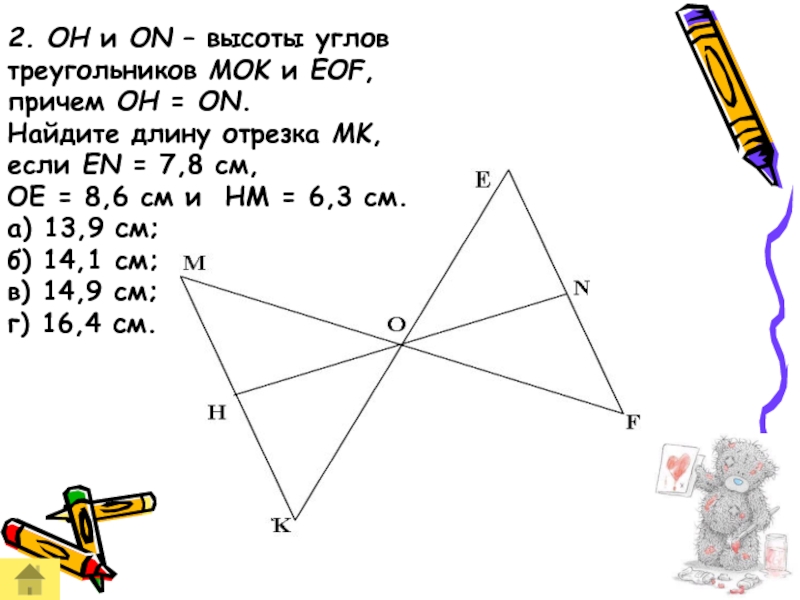
Слайд 442. OH и ON – высоты углов
треугольников MOK и EOF,
причем OH = ON.
Найдите длину отрезка MK,
если EN = 7,8 см,
OE = 8,6 см и HM = 6,3 см.
а) 13,9 см;
б) 14,1 см;
в) 14,9 см;
г) 16,4 см.
Слайд 453. Дано: ABC = DEF, LB=730,
BC = 6,9 см,
DF = 7,6 см,
Какое из высказываний верное?
а) DE = 6,9 см, АC = 7,6 см;
б) E = 730 АC = 7,6 см;
в) DF = 6,9см, E = 730;
г) AC = 7,6 см, D = 730
Какое из высказываний верное?
а) DE = 6,9 см, АC = 7,6 см;
б) E = 730 АC = 7,6 см;
в) DF = 6,9см, E = 730;
г) AC = 7,6 см, D = 730
4. Треугольник СDE равен треугольнику C1D1E1. Периметр треугольника СDE равен 76 см. Сторона C1D1 в 2,5 раза меньше стороны D1E1, а C1E1 на 8 см меньше стороны D1E1. Найдите большую сторону треугольника СDE.
а) 30 см; б) 28 см;
в) 35 см; г) 28 см.
Слайд 465. В треугольник ABC и KPM проведены две биссектрисы BO и
PE;
треугольник ABO равен треугольнику KPE.
Найдите отрезок EM,
если AC = 9 см, а EM < KE на 3,8 см.
а) 6,4 см; б) 5,4 см;
в) 2,6 см; г) 4,8 см.
треугольник ABO равен треугольнику KPE.
Найдите отрезок EM,
если AC = 9 см, а EM < KE на 3,8 см.
а) 6,4 см; б) 5,4 см;
в) 2,6 см; г) 4,8 см.
6. прямая MK разбивает плоскость на две полуплоскости. Из точек M и K в разные полуплоскости проведены равные отрезки MA и KB, причем угол AMK равен углу BKM.
Какие из высказываний верные:
1) AMB = AKB; 3) MKA = KMB;
2) LAKM = LBMK; 4) LAMB = LKBM?
а) 1; 3; 4; б) 1;2;4; в) 1;3; г) 2;3;
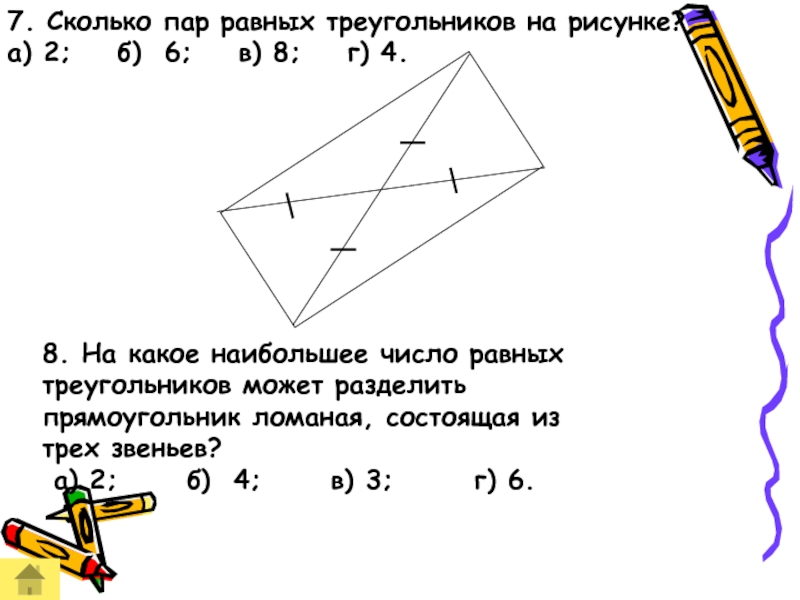
Слайд 477. Сколько пар равных треугольников на рисунке?
а) 2; б) 6;
в) 8; г) 4.
8. На какое наибольшее число равных треугольников может разделить прямоугольник ломаная, состоящая из трех звеньев?
а) 2; б) 4; в) 3; г) 6.
