- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многоугольники презентация
Содержание
- 1. Правильные многоугольники
- 2. Правильный многоугольник-это выпуклый многоугольник, у которого
- 3. В любой правильный многоугольник можно вписать окружность,
- 4. Формулы
- 6. Построение правильных многоугольников Построение вписанного в окружность
- 7. Построение правильного пятиугольника. 1)Постройте окружность, в которую
Слайд 1Правильные многоугольники
Степанян Арташес
Лицей №11 «Физтех»
Со времён Пифагора известны они.
В
Их встретим в орнаментах и на паркетах,
В стихотворениях разных поэтов.
И даже пчёлы с ними работают,
Строя в их форме домики-соты.
О. Панишева.
Слайд 2
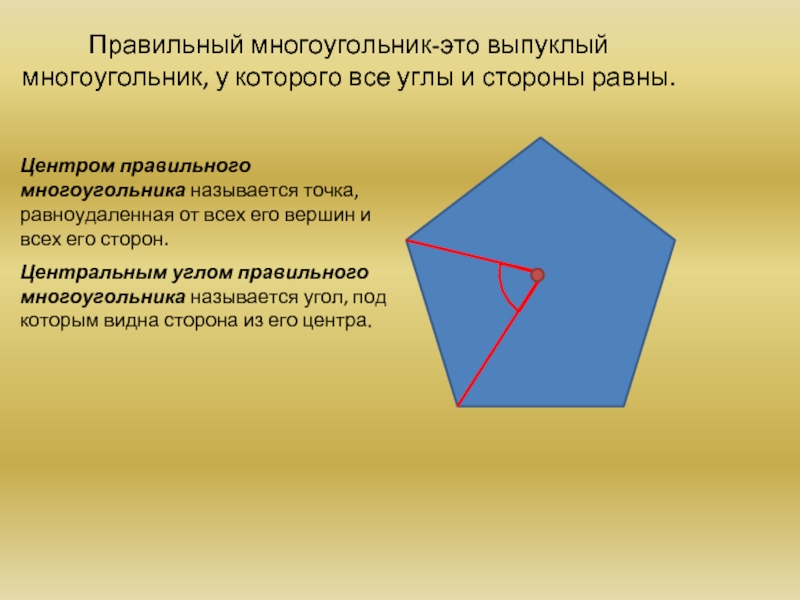
Правильный многоугольник-это выпуклый многоугольник, у которого все углы и стороны равны.
Центром
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
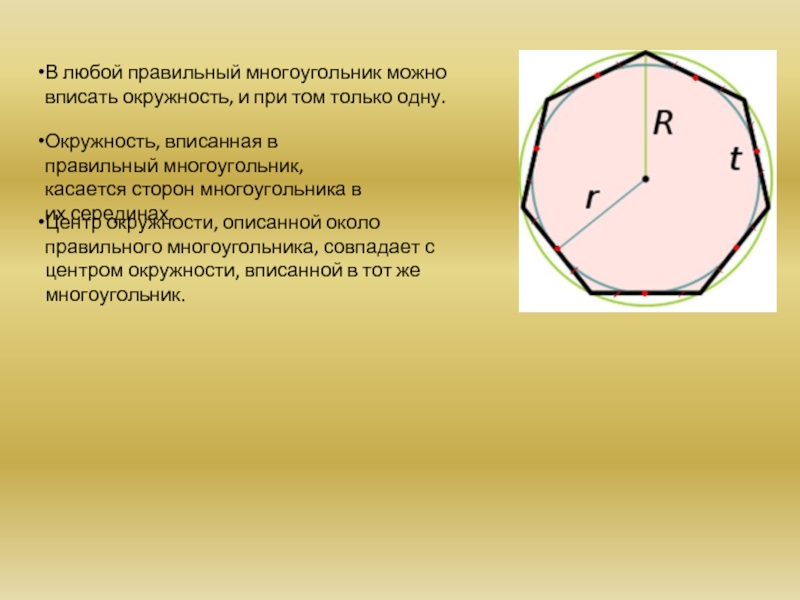
Слайд 3В любой правильный многоугольник можно вписать окружность, и при том только
Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
Слайд 6Построение правильных многоугольников
Построение вписанного в окружность правильного шестиугольника
Т.к. все стороны шестиугольника
а)На окружности а ставим ножку циркуля на точку 4 и чертим дугу, соединяющую точки 5 и 3
(аналогично с точками 1, 2 и 6).
б)Соединяем точки 1,2,3,4,5 и 6 соответственно.
Слайд 7Построение правильного пятиугольника.
1)Постройте окружность, в которую будет вписан пятиугольник и обозначьте
2)Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
3)Постройте с помощью циркуля прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью, как точку B.
4)Постройте с помощью циркуля точку C посередине между O и B.
Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
5)Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
6)Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
7)Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.