многоугольники, и в вершинах каждого многогранника сходится одинаковое число граней.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ презентация
Содержание
- 1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 2. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Правильные многогранники были известны еще
- 3. КОНСТРУКТОР Модели правильных многогранников можно изготовлять с
- 4. ТЕТРАЭДР Наиболее простым правильным многогранником является треугольная
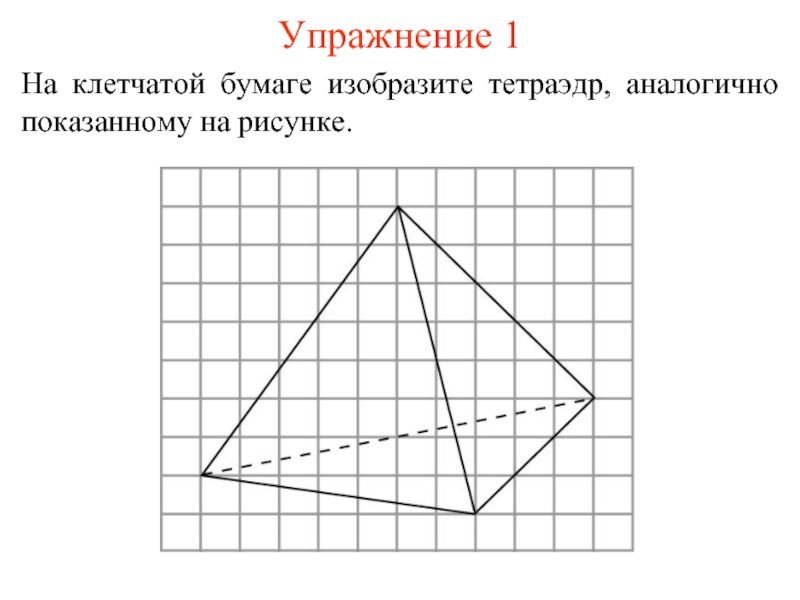
- 5. Упражнение 1 На клетчатой бумаге изобразите тетраэдр, аналогично показанному на рисунке.
- 6. КУБ (ГЕКСАЭДР) Многогранник, гранями которого являются квадраты
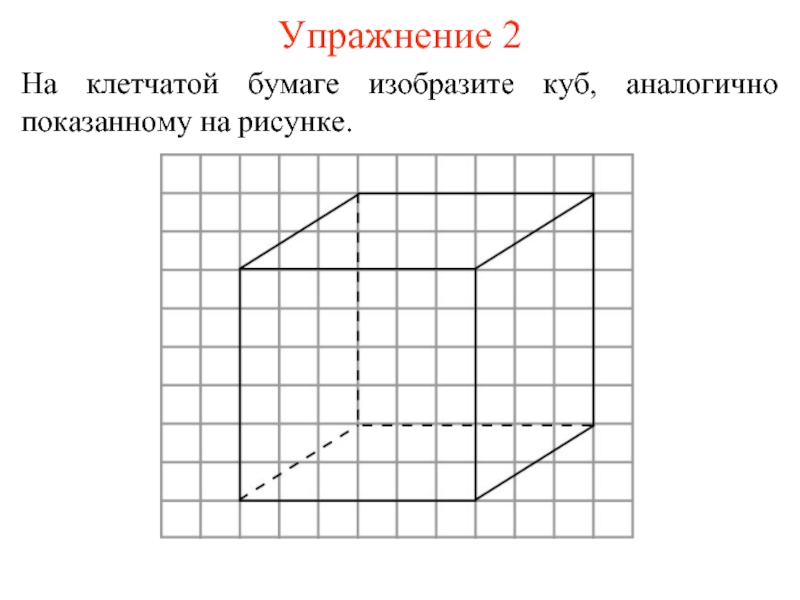
- 7. Упражнение 2 На клетчатой бумаге изобразите куб, аналогично показанному на рисунке.
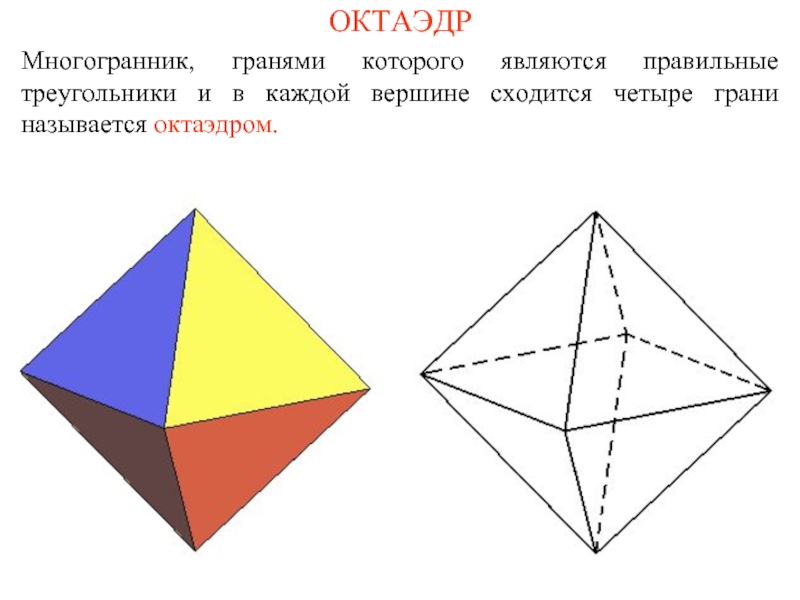
- 8. ОКТАЭДР Многогранник, гранями которого являются правильные треугольники
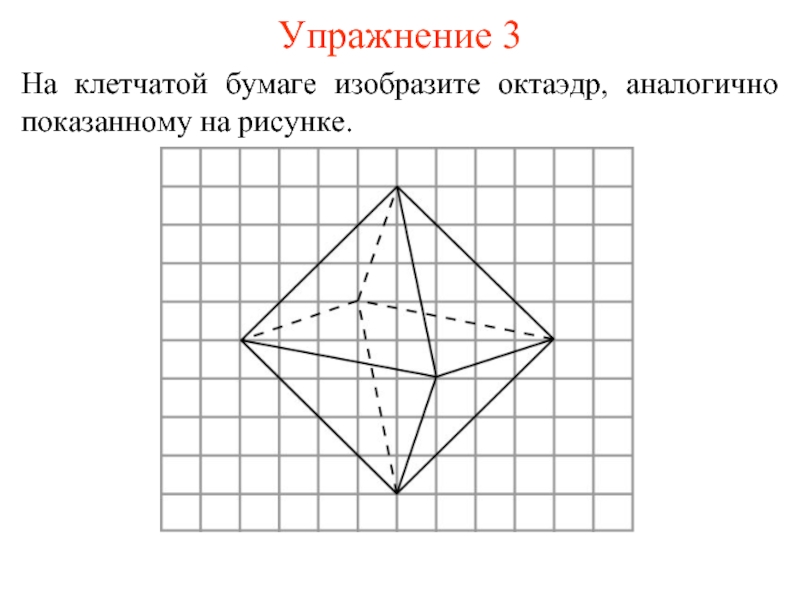
- 9. Упражнение 3 На клетчатой бумаге изобразите октаэдр, аналогично показанному на рисунке.
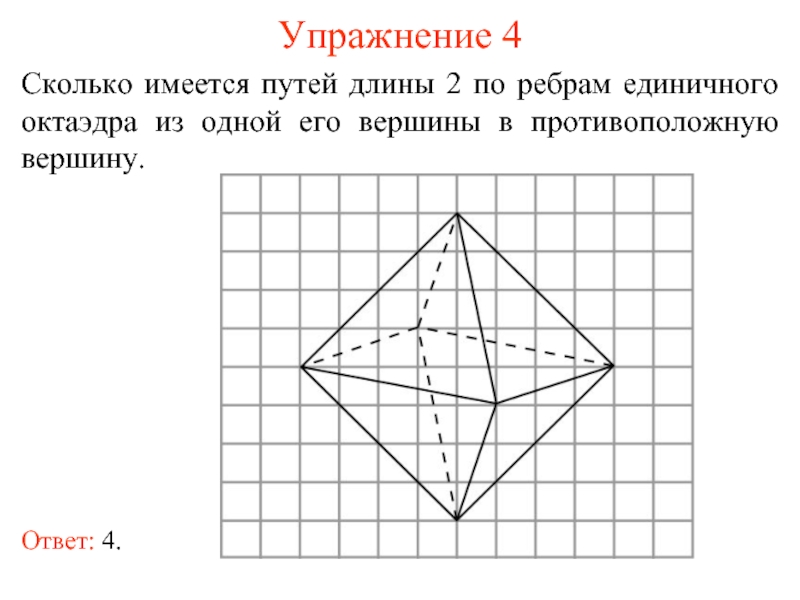
- 10. Упражнение 4 Сколько имеется путей длины 2
- 11. Упражнение 5 Сколько имеется путей длины 3
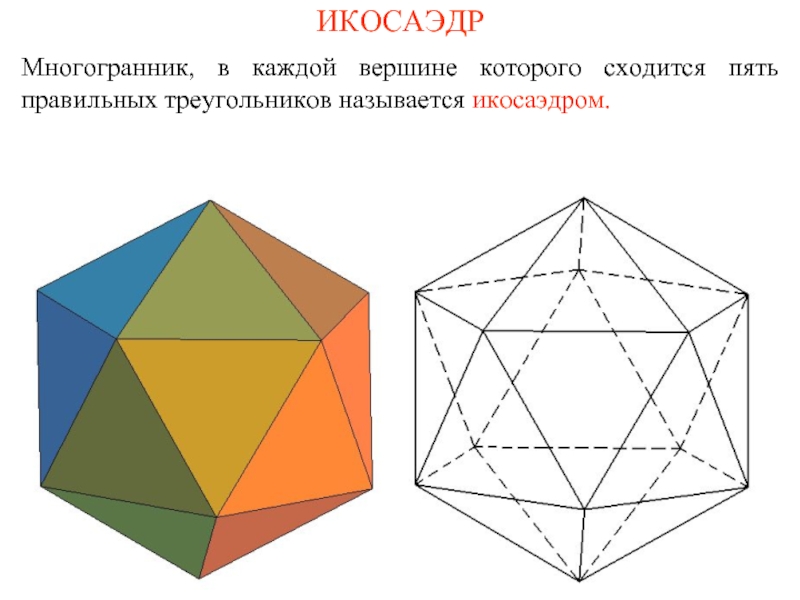
- 12. ИКОСАЭДР Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.
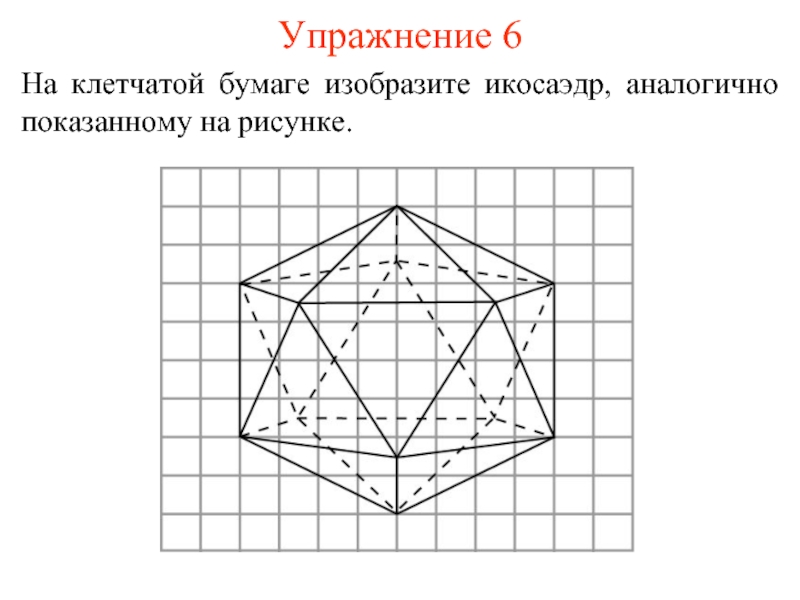
- 13. Упражнение 6 На клетчатой бумаге изобразите икосаэдр, аналогично показанному на рисунке.
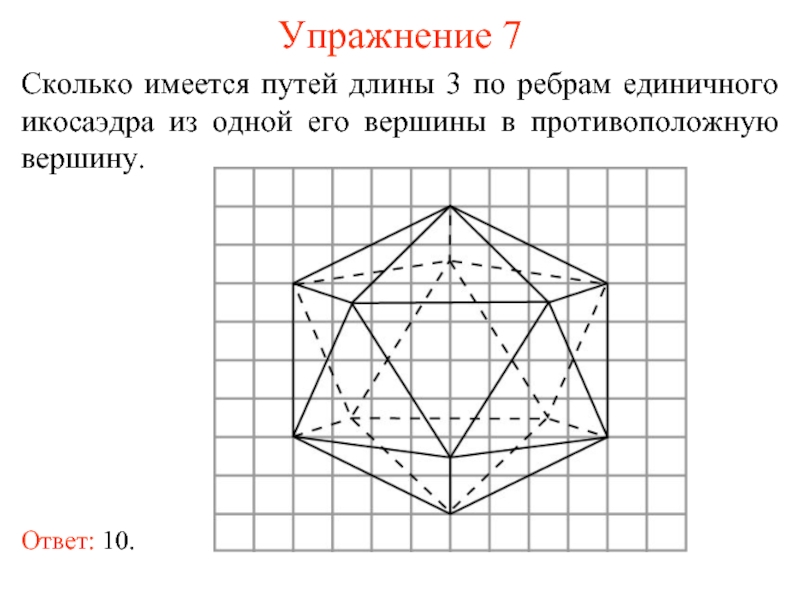
- 14. Упражнение 7 Сколько имеется путей длины 3
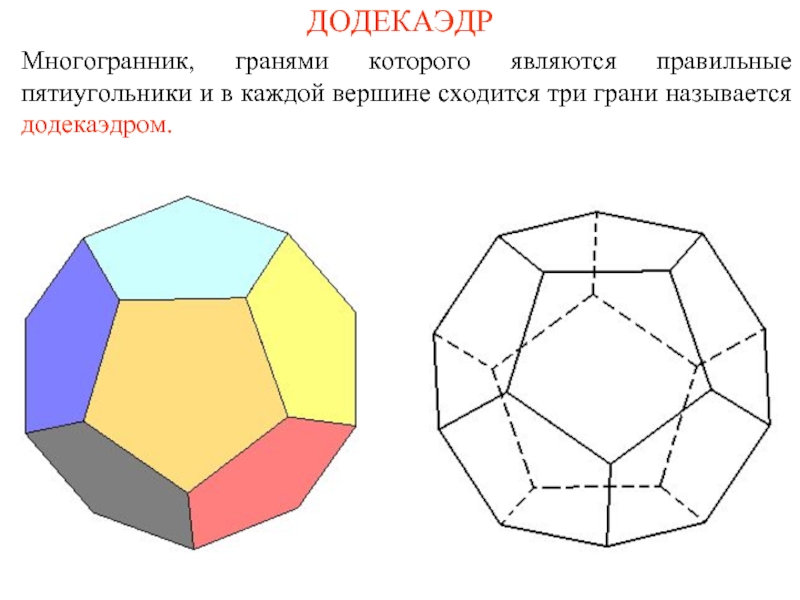
- 15. ДОДЕКАЭДР Многогранник, гранями которого являются правильные пятиугольники
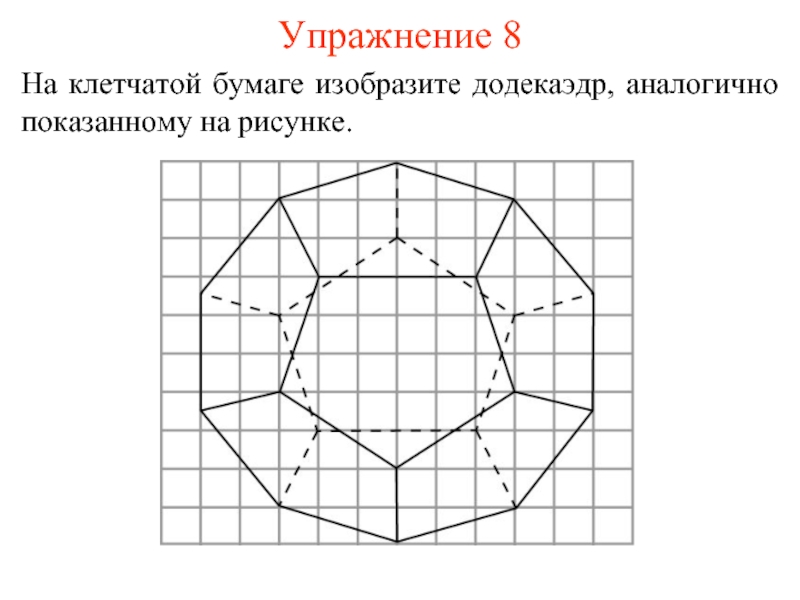
- 16. Упражнение 8 На клетчатой бумаге изобразите додекаэдр, аналогично показанному на рисунке.
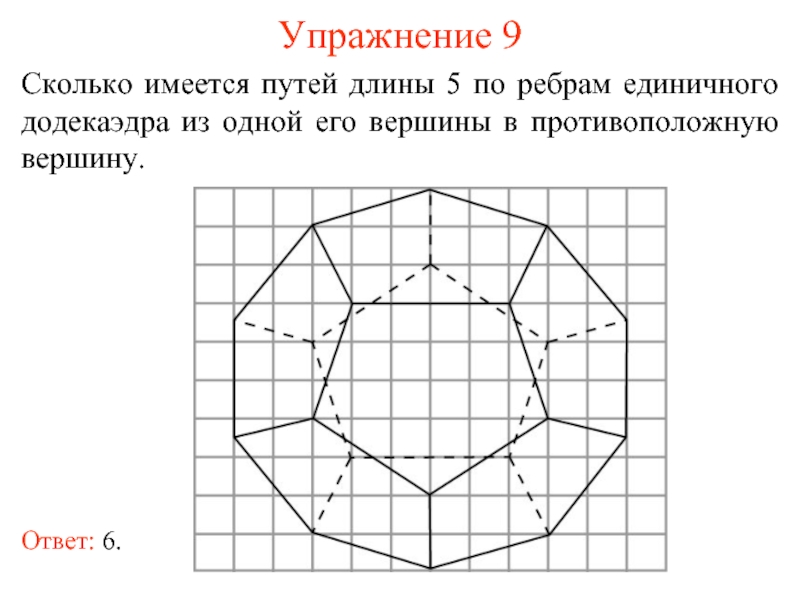
- 17. Упражнение 9 Сколько имеется путей длины 5
- 18. Упражнение 10 Сколько вершин (В), ребер (Р)
- 19. Упражнение 11 Окраска граней многогранника называется правильной,
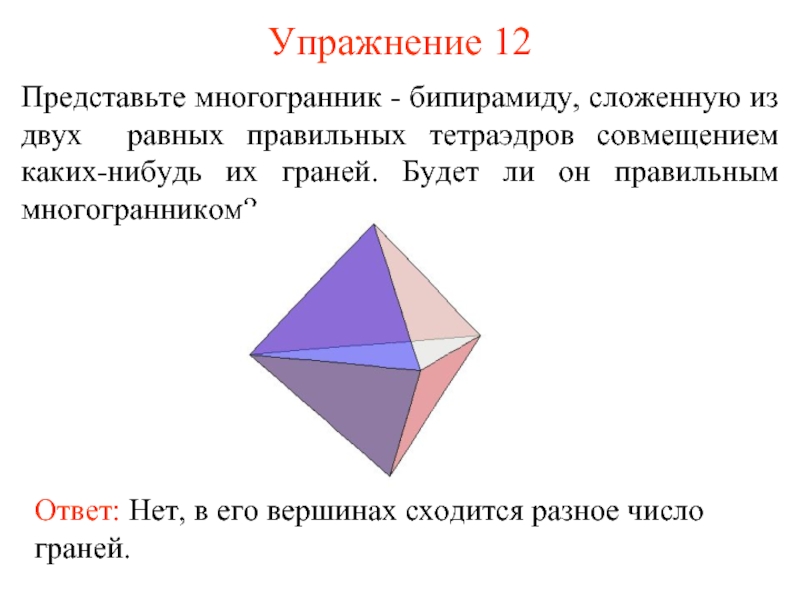
- 20. Упражнение 12 Представьте многогранник - бипирамиду, сложенную
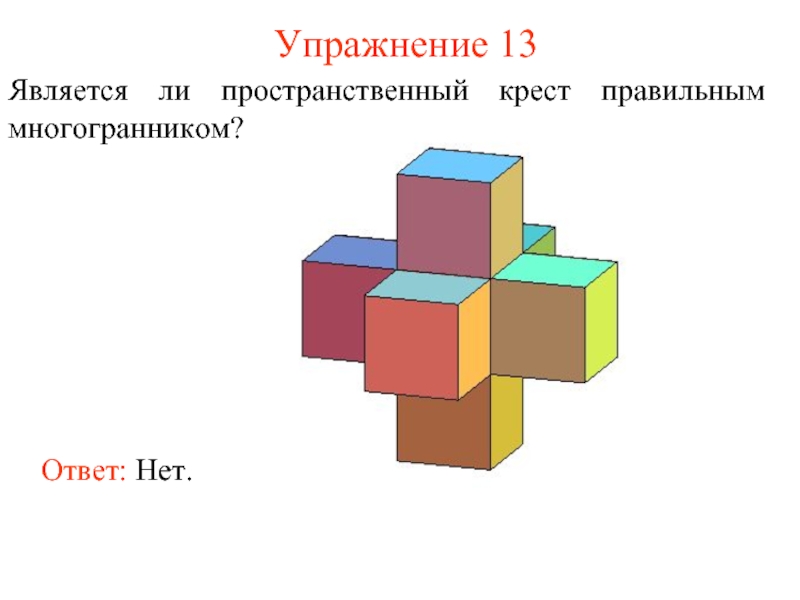
- 21. Упражнение 13 Является ли пространственный крест правильным многогранником? Ответ: Нет.
- 22. Упражнение 14 На рисунке изображен многогранник –
- 23. Упражнение 15 Сколько тетраэдров изображено на рисунке? Ответ: Пять.
- 24. Упражнение 16 Сколько кубов изображено на рисунке? Ответ: Три.
- 25. Упражнение 17 Сколько октаэдров изображено на рисунке? Ответ: Три.
- 26. Упражнение 18 Соединение каких двух правильных многогранников изображено на рисунке? Ответ: Куба и октаэдра.
- 27. Упражнение 19 Соединение каких двух правильных многогранников изображено на рисунке? Ответ: Икосаэдра и додекаэдра.
- 28. Упражнение 20 Соединение каких двух правильных многогранников изображено на рисунке? Ответ: Два икосаэдра.
- 29. Упражнение 21 Вершинами какого многогранника являются центры граней куба?
- 30. Упражнение 22 Вершинами какого многогранника являются центры граней октаэдра?
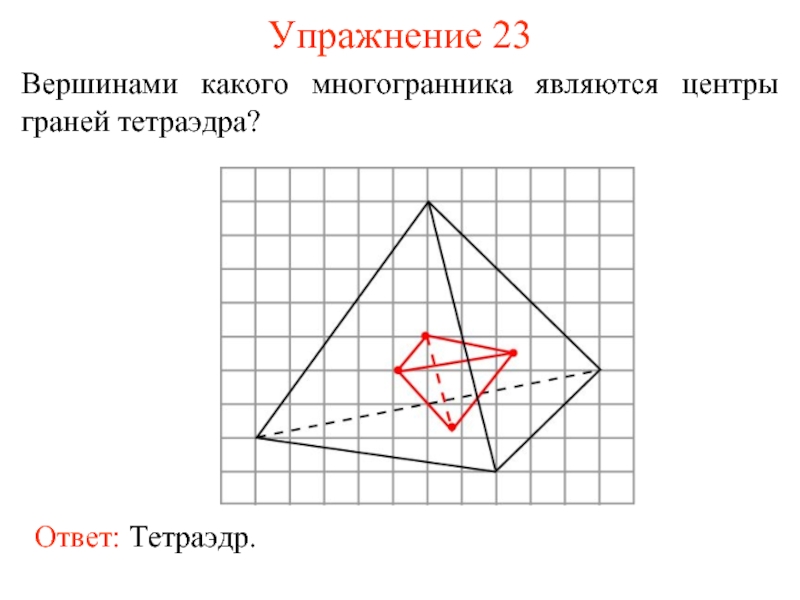
- 31. Упражнение 23 Вершинами какого многогранника являются центры граней тетраэдра?
- 32. Упражнение 24 Вершинами какого многогранника являются середины ребер тетраэдра?
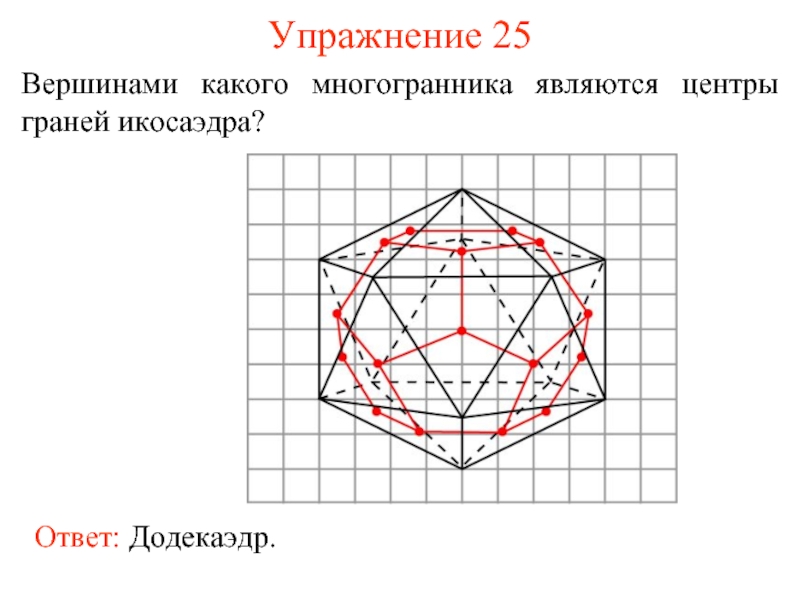
- 33. Упражнение 25 Вершинами какого многогранника являются центры граней икосаэдра?
- 34. Упражнение 26 Вершинами какого многогранника являются центры граней додекаэдра?
- 35. Упражнение 27 Какие из фигур, изображенных на
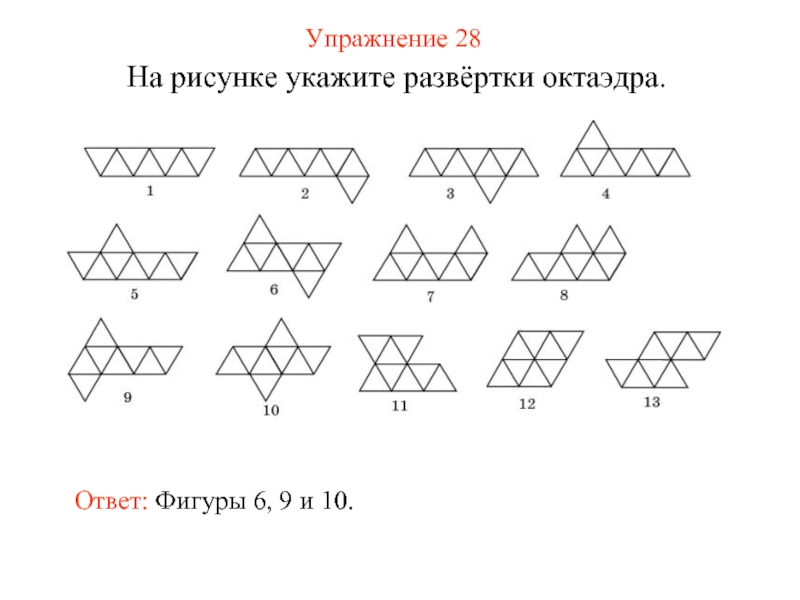
- 36. Упражнение 28 На рисунке укажите развёртки октаэдра. Ответ: Фигуры 6, 9 и 10.
- 37. Упражнение 29 Развертка какого многогранника изображена на рисунке? Ответ: Икосаэдра.
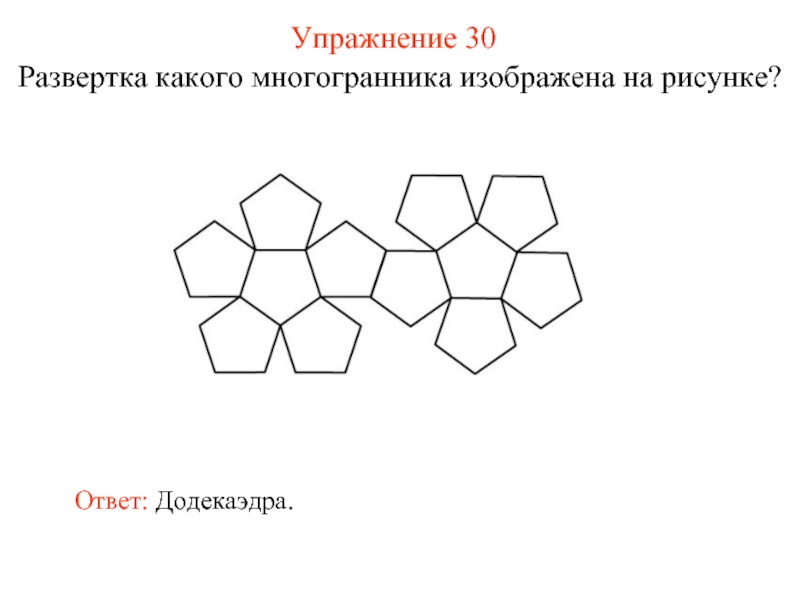
- 38. Упражнение 30 Развертка какого многогранника изображена на рисунке? Ответ: Додекаэдра.
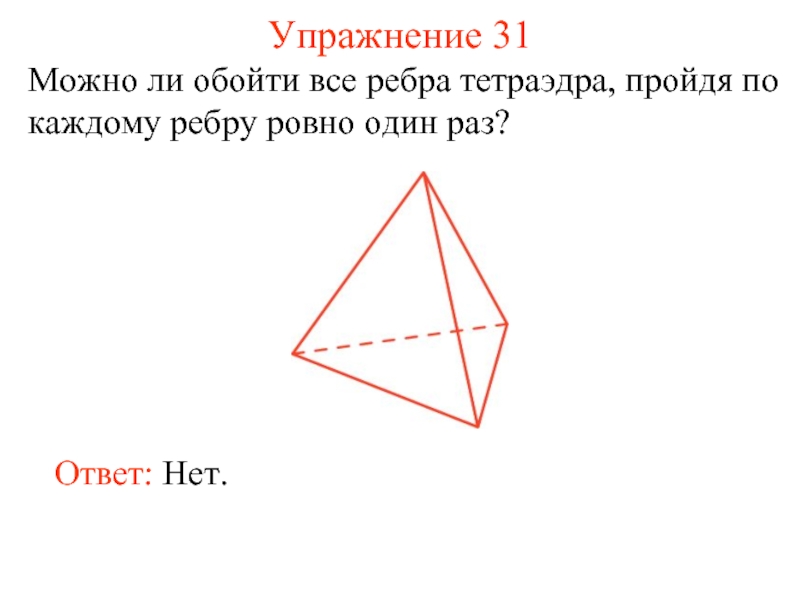
- 39. Упражнение 31 Можно ли обойти все ребра
- 40. Упражнение 32 Какое наименьшее число ребер придется
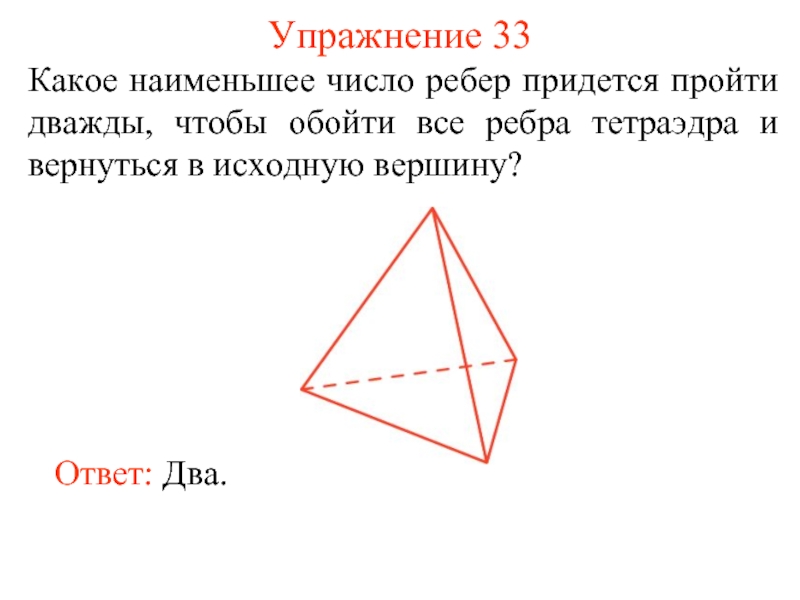
- 41. Упражнение 33 Какое наименьшее число ребер придется
- 42. Упражнение 34 Можно ли обойти все ребра
- 43. Упражнение 35 Какое наименьшее число ребер придется
- 44. Упражнение 36 Какое наименьшее число ребер придется
- 45. Упражнение 37 Можно ли обойти все ребра
- 46. Упражнение 38 Можно ли обойти все ребра
- 47. Упражнение 39 Какое наименьшее число ребер придется
- 48. Упражнение 40 Какое наименьшее число ребер придется
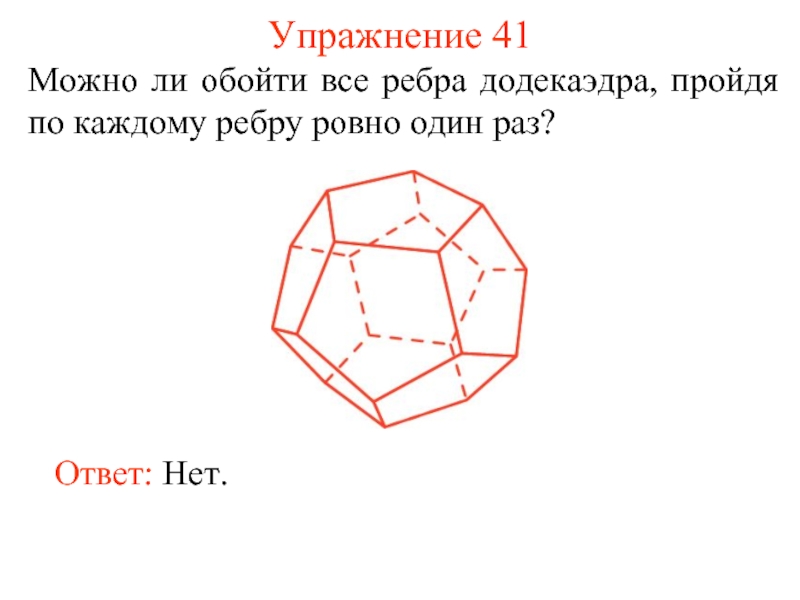
- 49. Упражнение 41 Можно ли обойти все ребра
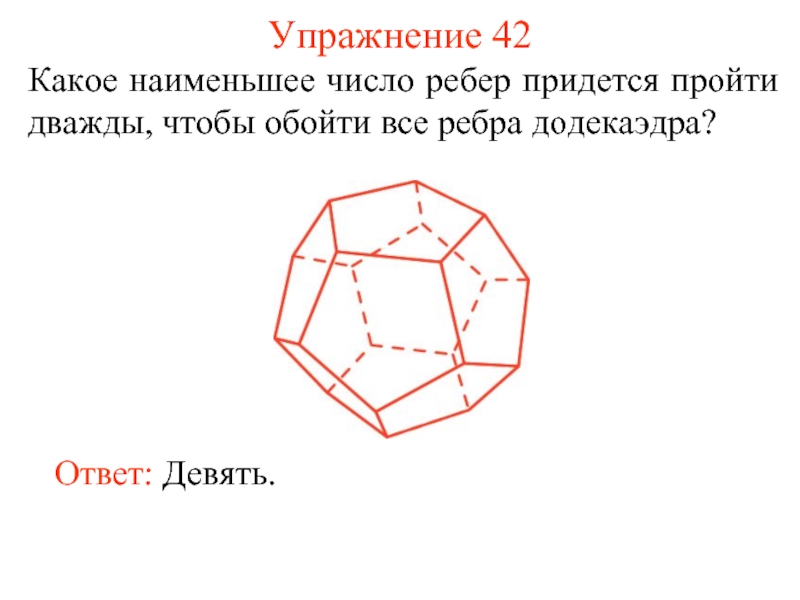
- 50. Упражнение 42 Какое наименьшее число ребер придется
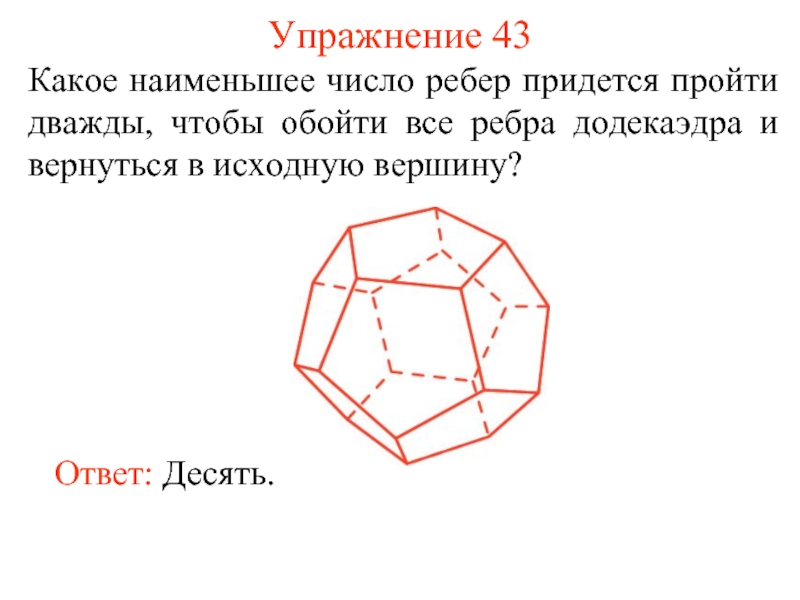
- 51. Упражнение 43 Какое наименьшее число ребер придется
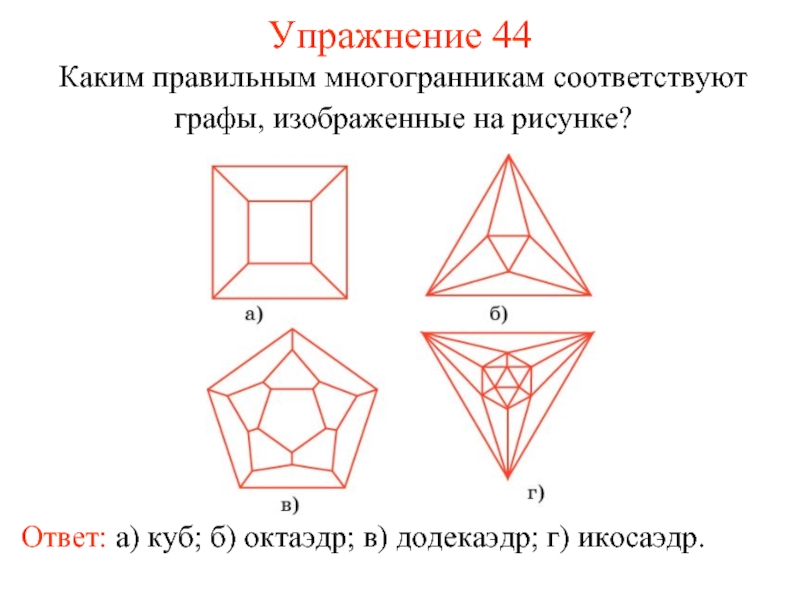
- 52. Упражнение 44 Каким правильным многогранникам соответствуют графы,
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Правильные многогранники были известны еще в древней Греции. Пифагор и его ученики считали, что все состоит из атомов, имеющих форму правильных многогранников. В частности, атомы огня имеют форму тетраэдра
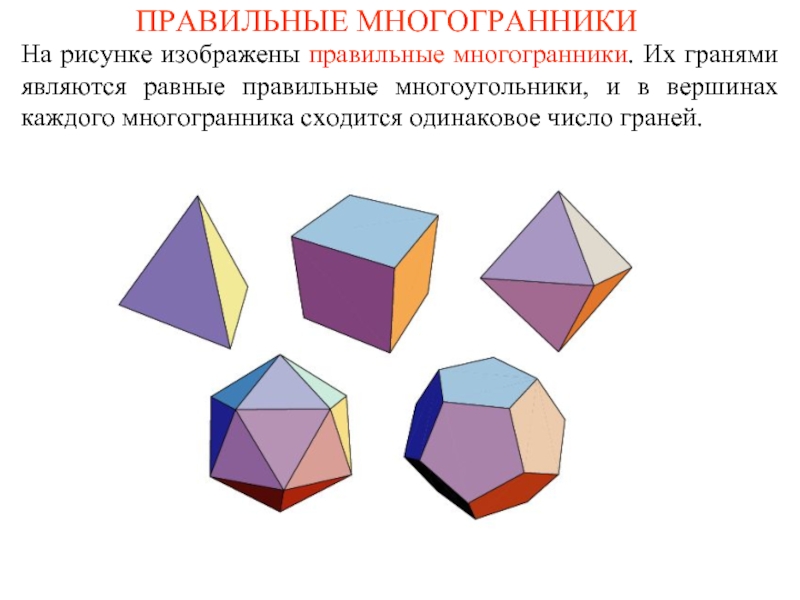
Слайд 1ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
На рисунке изображены правильные многогранники. Их гранями являются равные правильные
Слайд 2ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Правильные многогранники были известны еще в древней Греции. Пифагор и
его ученики считали, что все состоит из атомов, имеющих форму правильных многогранников. В частности, атомы огня имеют форму тетраэдра (его гранями являются четыре правильных треугольника (рис. а); земли - гексаэдра (куб – многогранник, гранями которого являются шесть квадратов, рис. б); воздуха – октаэдра (его гранями являются восемь правильных треугольников, рис. в); воды – икосаэдра (его гранями являются двадцать правильных треугольников, рис. г); вся Вселенная, по мнению древних, имела форму додекаэдра (его гранями являются двенадцать правильных пятиугольников, рис. д).
Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.
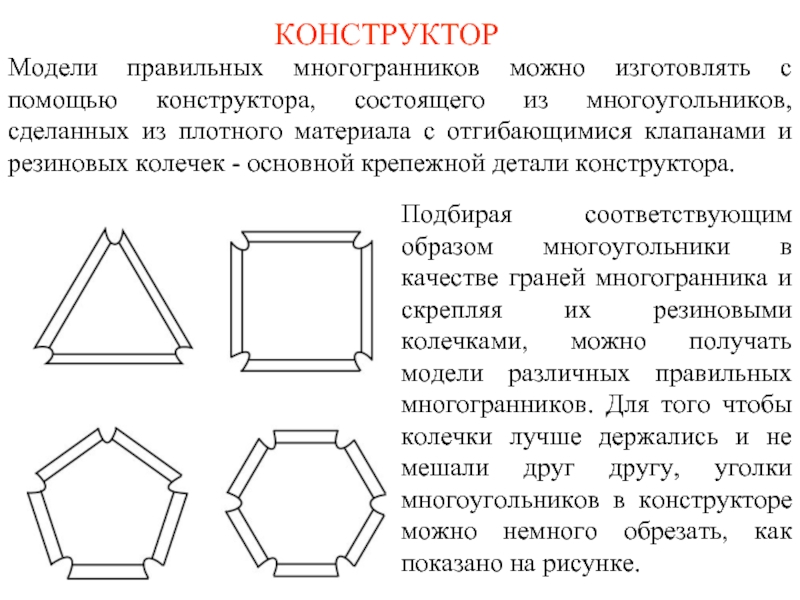
Слайд 3КОНСТРУКТОР
Модели правильных многогранников можно изготовлять с помощью конструктора, состоящего из многоугольников,
сделанных из плотного материала с отгибающимися клапанами и резиновых колечек - основной крепежной детали конструктора.
Подбирая соответствующим образом многоугольники в качестве граней многогранника и скрепляя их резиновыми колечками, можно получать модели различных правильных многогранников. Для того чтобы колечки лучше держались и не мешали друг другу, уголки многоугольников в конструкторе можно немного обрезать, как показано на рисунке.
Слайд 4ТЕТРАЭДР
Наиболее простым правильным многогранником является треугольная пирамида, грани которой правильные треугольники.
В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.
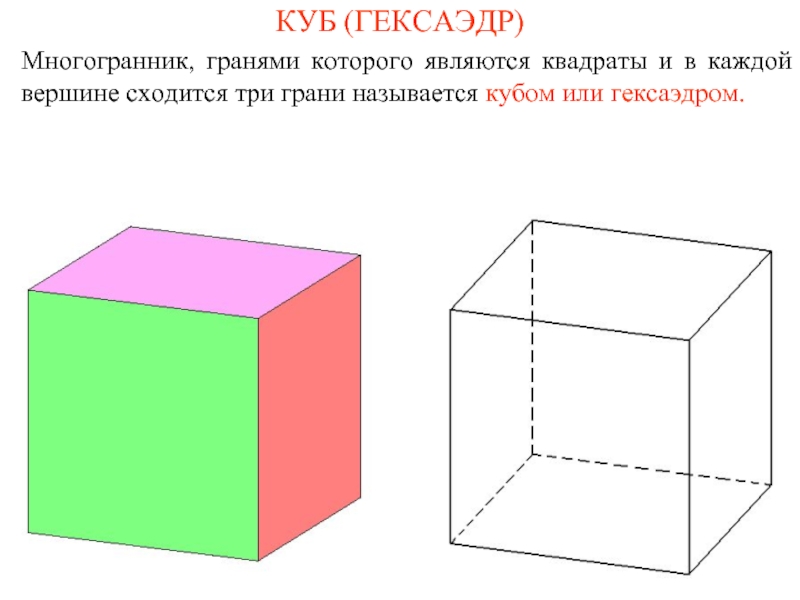
Слайд 6КУБ (ГЕКСАЭДР)
Многогранник, гранями которого являются квадраты и в каждой вершине сходится
три грани называется кубом или гексаэдром.
Слайд 8ОКТАЭДР
Многогранник, гранями которого являются правильные треугольники и в каждой вершине сходится
четыре грани называется октаэдром.
Слайд 10Упражнение 4
Сколько имеется путей длины 2 по ребрам единичного октаэдра из
одной его вершины в противоположную вершину.
Ответ: 4.
Слайд 11Упражнение 5
Сколько имеется путей длины 3 по ребрам единичного октаэдра из
одной его вершины в противоположную вершину.
Ответ: 8.
Слайд 12ИКОСАЭДР
Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.
Слайд 14Упражнение 7
Сколько имеется путей длины 3 по ребрам единичного икосаэдра из
одной его вершины в противоположную вершину.
Ответ: 10.
Слайд 15ДОДЕКАЭДР
Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходится
три грани называется додекаэдром.
Слайд 17Упражнение 9
Сколько имеется путей длины 5 по ребрам единичного додекаэдра из
одной его вершины в противоположную вершину.
Ответ: 6.
Слайд 18Упражнение 10
Сколько вершин (В), ребер (Р) и граней (Г) имеют:
а) тетраэдр;
б)
куб;
в) октаэдр;
г) икосаэдр;
д) додекаэдр?
в) октаэдр;
г) икосаэдр;
д) додекаэдр?
Ответ: а) В = 4, Р = 6, Г = 4;
б) В = 8, Р = 12, Г = 6;
в) В = 6, Р = 12, Г = 8;
г) В = 12, Р = 30, Г = 20;
д) В = 20, Р = 30, Г = 12.
Слайд 19Упражнение 11
Окраска граней многогранника называется правильной, если соседние грани имеют разные
цвета. Какое минимальное число красок потребуется для правильной окраски граней:
Ответ: 4.
а) тетраэдра;
б) куба;
в) октаэдра;
г) икосаэдра;
д) додекаэдра?
Ответ: 3.
Ответ: 2.
Ответ: 3.
Ответ: 4.
Слайд 20Упражнение 12
Представьте многогранник - бипирамиду, сложенную из двух равных правильных тетраэдров
совмещением каких-нибудь их граней. Будет ли он правильным многогранником?
Ответ: Нет, в его вершинах сходится разное число граней.
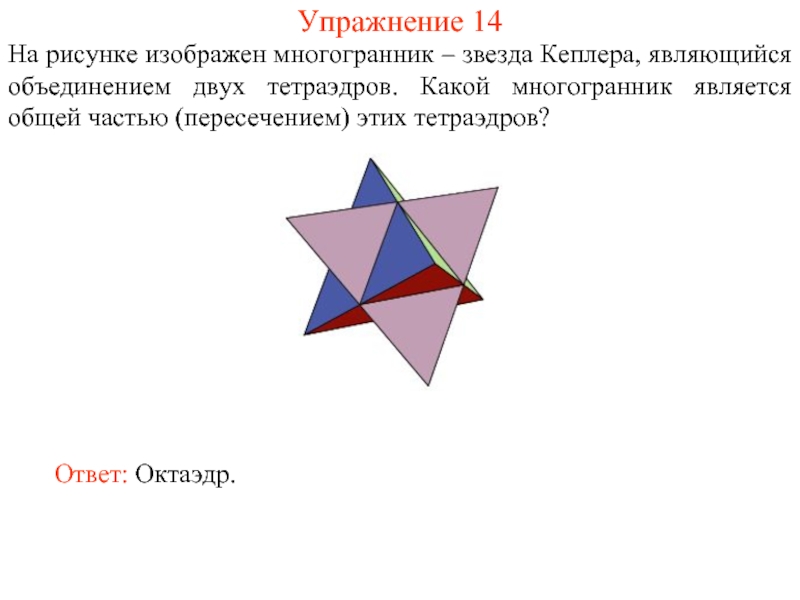
Слайд 22Упражнение 14
На рисунке изображен многогранник – звезда Кеплера, являющийся объединением двух
тетраэдров. Какой многогранник является общей частью (пересечением) этих тетраэдров?
Ответ: Октаэдр.
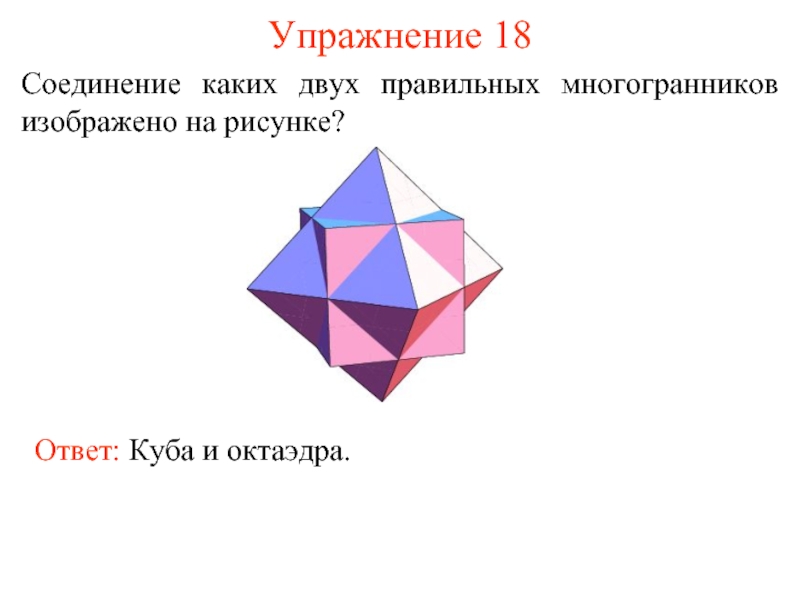
Слайд 26Упражнение 18
Соединение каких двух правильных многогранников изображено на рисунке?
Ответ: Куба и
октаэдра.
Слайд 27Упражнение 19
Соединение каких двух правильных многогранников изображено на рисунке?
Ответ: Икосаэдра и
додекаэдра.
Слайд 28Упражнение 20
Соединение каких двух правильных многогранников изображено на рисунке?
Ответ: Два икосаэдра.
Слайд 35Упражнение 27
Какие из фигур, изображенных на рисунке не являются развёртками правильного
тетраэдра?
Ответ: Фигура 3, так как у неё имеется точка, в которой сходится четыре треугольника, а у тетраэдра имеются только вершины, в которых сходится по три ребра.
Слайд 39Упражнение 31
Можно ли обойти все ребра тетраэдра, пройдя по каждому ребру
ровно один раз?
Ответ: Нет.
Слайд 40Упражнение 32
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра тетраэдра?
Ответ: Одно.
Слайд 41Упражнение 33
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра тетраэдра и вернуться в исходную вершину?
Ответ: Два.
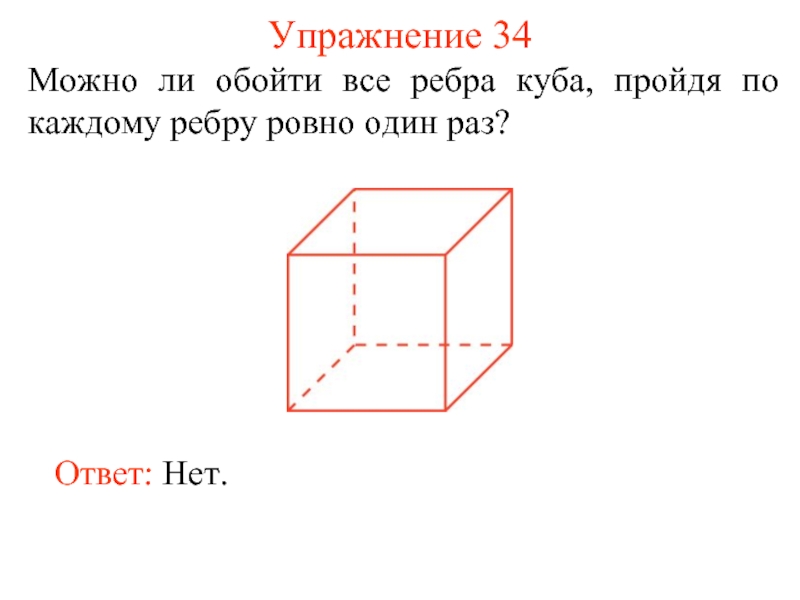
Слайд 42Упражнение 34
Можно ли обойти все ребра куба, пройдя по каждому ребру
ровно один раз?
Ответ: Нет.
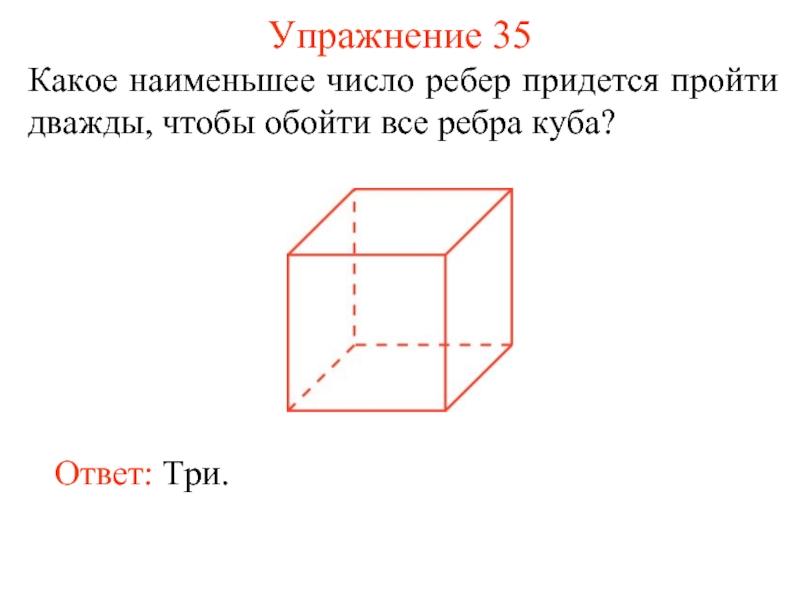
Слайд 43Упражнение 35
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра куба?
Ответ: Три.
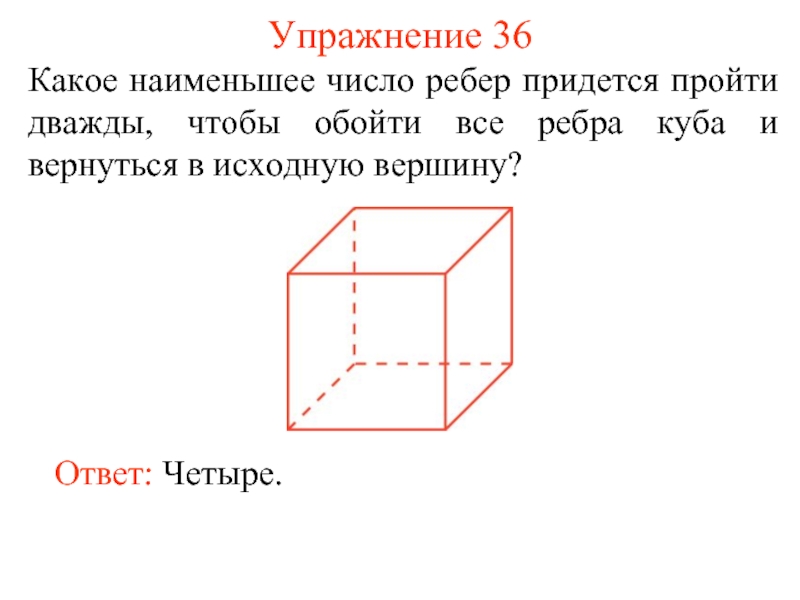
Слайд 44Упражнение 36
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра куба и вернуться в исходную вершину?
Ответ: Четыре.
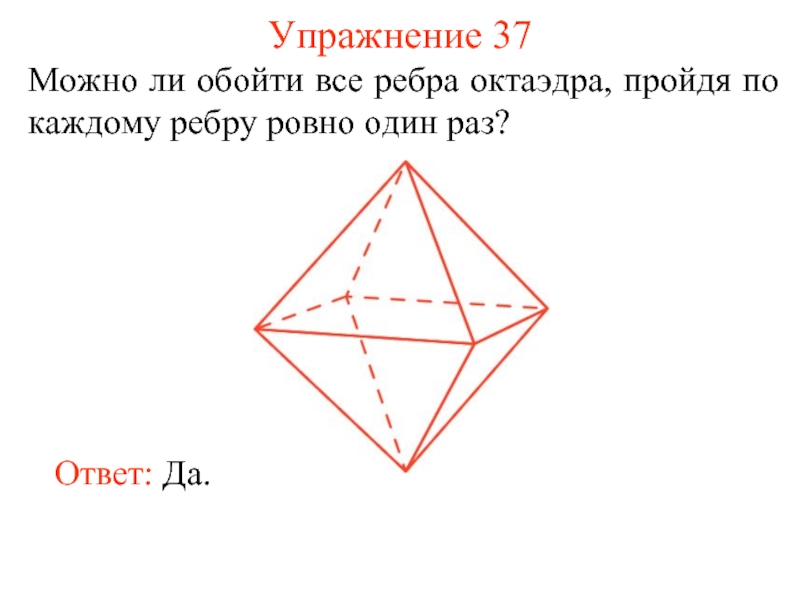
Слайд 45Упражнение 37
Можно ли обойти все ребра октаэдра, пройдя по каждому ребру
ровно один раз?
Ответ: Да.
Слайд 46Упражнение 38
Можно ли обойти все ребра икосаэдра, пройдя по каждому ребру
ровно один раз?
Ответ: Нет.
Слайд 47Упражнение 39
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра икосаэдра?
Ответ: Пять.
Слайд 48Упражнение 40
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра икосаэдра и вернуться в исходную вершину?
Ответ: Шесть.
Слайд 49Упражнение 41
Можно ли обойти все ребра додекаэдра, пройдя по каждому ребру
ровно один раз?
Ответ: Нет.
Слайд 50Упражнение 42
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра додекаэдра?
Ответ: Девять.
Слайд 51Упражнение 43
Какое наименьшее число ребер придется пройти дважды, чтобы обойти все
ребра додекаэдра и вернуться в исходную вершину?
Ответ: Десять.
Слайд 52Упражнение 44
Каким правильным многогранникам соответствуют графы, изображенные на рисунке?
Ответ: а)
куб; б) октаэдр; в) додекаэдр; г) икосаэдр.
