- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ презентация
Содержание
- 1. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- 2. Цель проекта: Познакомиться с правильными многогранниками.
- 3. ЗАДАЧИ: Развивать эстетическое восприятие математический фактов,
- 4. МЕТОДЫ: Работа с литературой. Работа с интернет-ресурсами. Беседа с преподавателем математики. Наблюдение.
- 5. Виды многогранников Многогранник- это поверхность составленная из
- 6. Многогранники Однородные выпуклые Однородные
- 7. Правильными многогранниками называют выпуклые многогранники, все
- 8. Существует лишь пять выпуклых правильных многогранников
- 9. огонь тетраэдр икосаэдр
- 10. Тетраэдр -правильный четырехгранник. Он ограничен
- 11. Гексаэдр - правильный шестигранник. Это куб состоящий из шести равных квадратов.
- 12. Октаэдр -правильный восьмигранник. Он
- 13. Додекаэдр -правильный двенадцатигранник, состоит из
- 14. Икосаэдр -состоит из 20
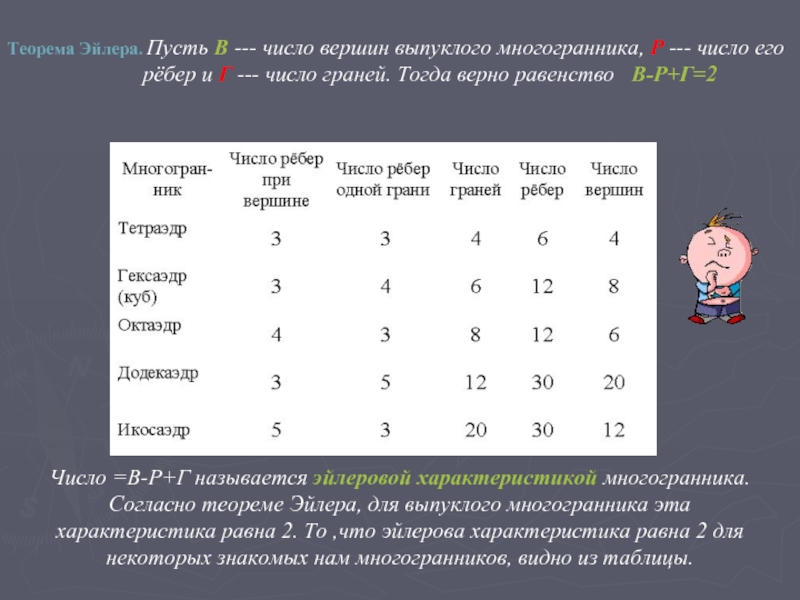
- 15. Число =В-Р+Г называется эйлеровой характеристикой многогранника. Согласно
- 16. Правильные многогранники - самые выгодные фигуры. И
- 17. Молекула МЕТАНА имеет форму правильного тетраэдра. Этот
- 18. Кристаллы поваренной соли имеют форму куба,
- 19. Форму одноклеточных организмов –
- 20. Пятничный многогранник: “огуречный” вирус На картинке
- 21. ДНК ДНК генетического кода жизни –
- 22. Искусство впрочем, многогранники - отнюдь не
- 23. Так как правильные многогранники обладают жесткостью, то
- 24. Кто был в Москве, знает, как красив
Слайд 1ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Работу выполнили ученицы 10 класса школы №26 Невского района г.Санкт-Петербурга
Агапова
Слайд 2Цель проекта:
Познакомиться с правильными многогранниками.
Изучить их формы и узнать где
Исследовать практическое применение многогранников.
Слайд 3ЗАДАЧИ:
Развивать эстетическое восприятие математический фактов, расширить представление о сфере применения математики.
Расширить
Проследить историю развития многогранников.
Исследовать проявление и применение геометрии в природе и различных сферах деятельности человека.
Слайд 4МЕТОДЫ:
Работа с литературой.
Работа с интернет-ресурсами.
Беседа с преподавателем математики.
Наблюдение.
Слайд 5Виды многогранников
Многогранник- это поверхность составленная из многоугольников, а также тело ограниченное
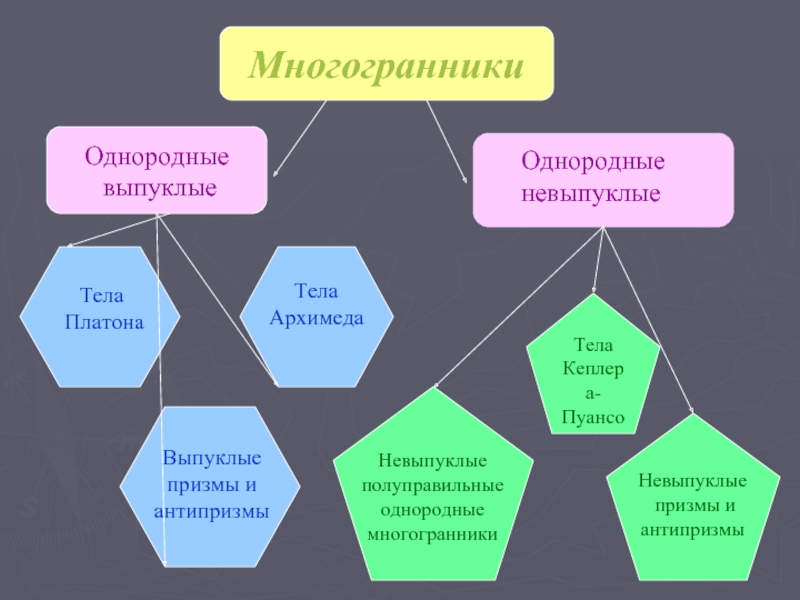
Слайд 6Многогранники
Однородные
выпуклые
Однородные
Тела
Архимеда
Тела
Платона
Выпуклые
призмы и
антипризмы
Тела
Кеплера-
Пуансо
Невыпуклые
полуправильные
однородные
многогранники
Невыпуклые
призмы и
антипризмы
Слайд 7Правильными многогранниками
называют выпуклые многогранники, все грани и все
В каждой вершине правильного многогранника сходится одно и то же число рёбер .
Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны.
Правильные многогранники - трехмерный аналог плоских правильных многоугольников.
Слайд 8 Существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и
Эти тела еще называют
телами Платона.
Слайд 9 огонь
тетраэдр
икосаэдр
октаэдр
гексаэдр
вселенная
додекаэдр
вода
земля
воздух
Платон предположил, что атомы четырех «основных элементов» (земля, вода,
Частицы трех стихий, которые легко превращаются друг в друг, а именно огонь, воздух и вода, оказались составленными из одинаковых фигур – правильных треугольников. А земля, существенно отличающаяся от них, состоит из частиц другого вида – кубов, а точнее квадратов.
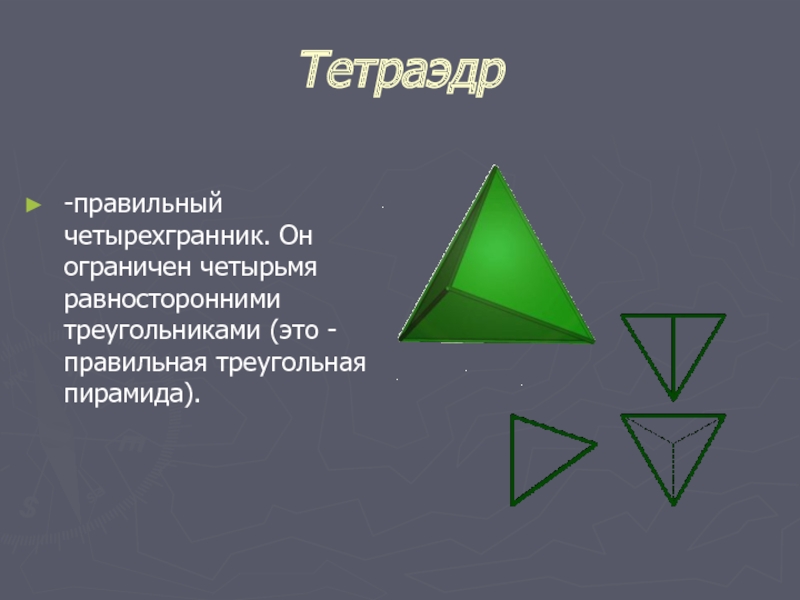
Слайд 10Тетраэдр
-правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это - правильная
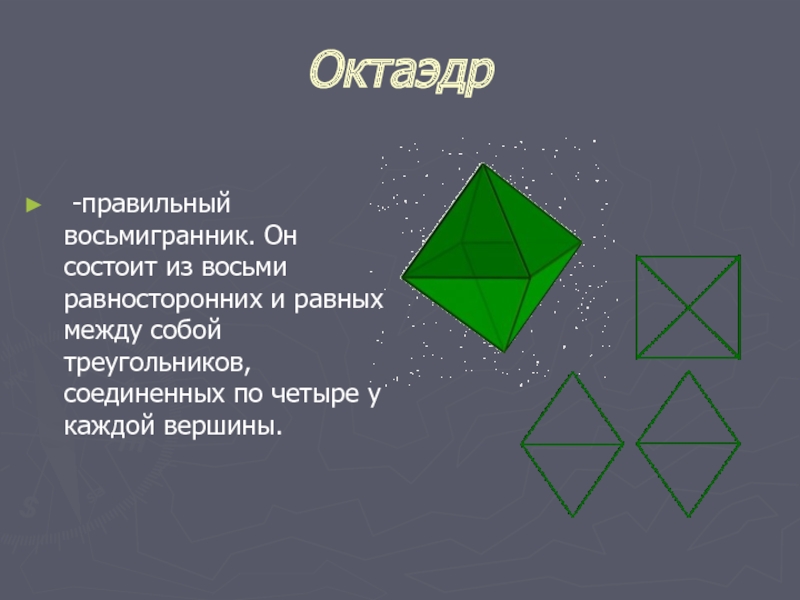
Слайд 12Октаэдр
-правильный восьмигранник. Он состоит из восьми равносторонних и равных
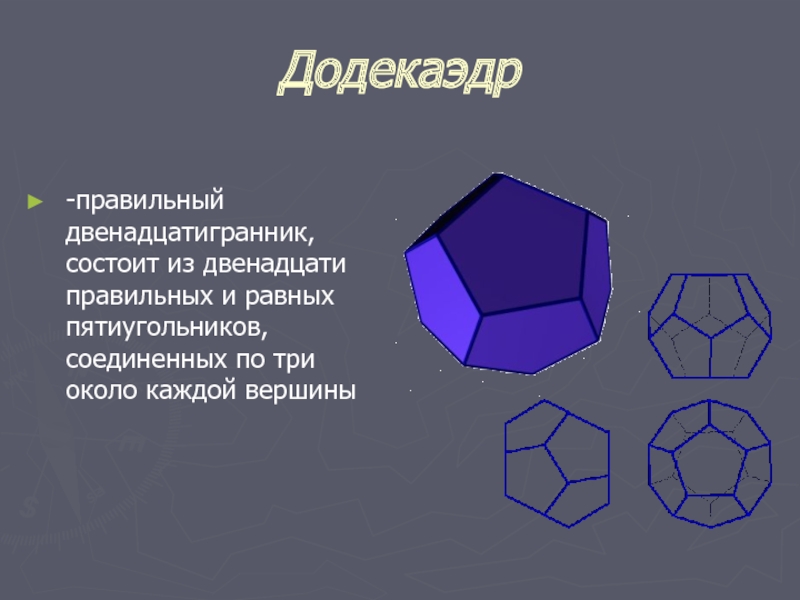
Слайд 13Додекаэдр
-правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных
Слайд 14Икосаэдр
-состоит из 20 равносторонних и равных треугольников, соединенных по пять
Слайд 15Число =В-Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого
Слайд 16Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется.
Слайд 17Молекула МЕТАНА имеет форму правильного
тетраэдра.
Этот факт подтверждается фотографиями молекулы
метана, полученными при
микроскопа.
Эта форма — следствие упорядоченного расположения в кристалле атомов, образующих трёхмерно-периодическую пространственную укладку — кристаллическую решетку.
Кристаллы
Слайд 18Кристаллы поваренной соли имеют форму куба, кристаллы льда и горного хрусталя
Алмаз чаще всего встречается в виде октаэдра, иногда куба.
Исландский шпат, который раздваивает изображение, имеет форму косого параллелепипеда.
Кварц
Кристалл поваренной соли
Слайд 19 Форму одноклеточных организмов – феодарий точно передает икосаэдр.
Чем же вызвана такая природная геометризация? Может быть, тем, что из всех многогранников с таким же количеством граней именно икосаэдр имеет наибольший объем и наименьшую площадь поверхности. Это геометрическое свойство помогает морскому микроорганизму преодолевать давление водной толщи.
Одноклеточные организмы
Слайд 20 Пятничный многогранник: “огуречный” вирус На картинке – вирус, поражающий ценные растения типа
Именно икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее.
Вирусы
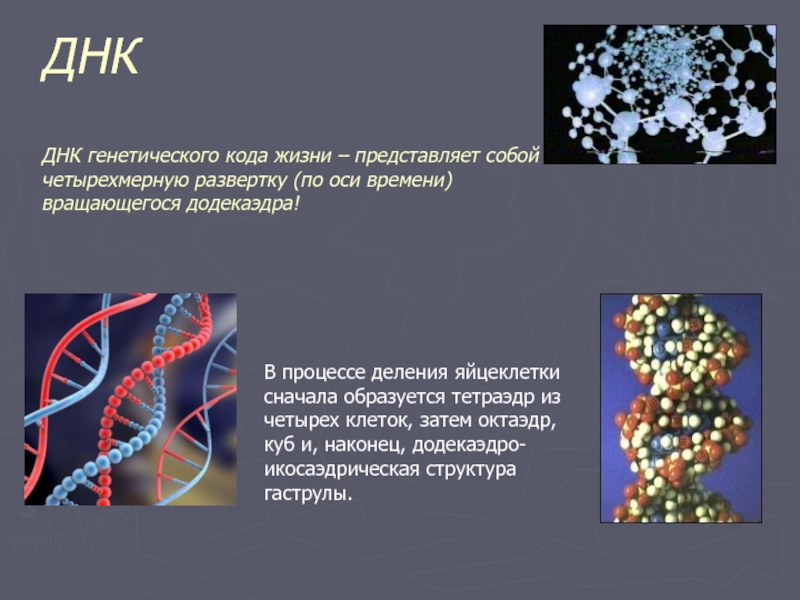
Слайд 21ДНК ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси
В процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, додекаэдро-икосаэдрическая структура гаструлы.
Слайд 22Искусство впрочем, многогранники - отнюдь не только объект научных исследований. Их
Гравюра. Звезды.
Слайд 23Так как правильные многогранники обладают жесткостью, то каркасы куполов церквей делают
Многогранники
в архитектуре
Слайд 24Кто был в Москве, знает, как красив Кремль. Прекрасны его башни! Сколько
Набатная башня Кремля составлена из нескольких параллелепипедов. На высоком параллелепипеде стоит параллелепипед поменьше, с проемами для окон, а еще выше воздвигнута четырехугольная усеченная пирамида. На ней расположены четыре арки, увенчанные восьмиугольной пирамидой.