Учитель математики
муниципального бюджетного общеобразовательного учреждения
«Удомельская средняя общеобразовательная школа №5 с углублённым изучением отдельных предметов»
Летунова Наталья Владимировна
2015 г
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Повышение качества математического (геометрического) образования на уроках наглядной геометрии в 5-6 классах.Часть 1 5 класс презентация
Содержание
- 1. Повышение качества математического (геометрического) образования на уроках наглядной геометрии в 5-6 классах.Часть 1 5 класс
- 2. Мир геометрии окружает нас
- 3. Чтобы научить детей внимательно
- 4. Преподавание ведется по
- 5. Пособие содержит уникальный задачный материал
- 6. На первом занятии мы
- 7. Изумлению пятиклассников нет предела, когда им
- 8. Закономерна следующая тема: «Пространство и размерность»
- 9. Затем перед ребятами ставится проблема:
- 10. Перспектива Картинка венгерского художника Виктора Вазарели
- 11. Перспектива и иллюзии Помогает с помощью изгибов
- 12. Пятиклассники учатся работать с чертёжными инструментами. Транспортиром
- 13. Особое внимание уделяется кубу и его свойствам Клеим куб из разверток
- 14. Особое внимание уделяется кубу и его свойствам
- 15. Помогают развивать геометрическую зоркость рисунки с неоднозначными
- 16. Помогают развивать геометрическую зоркость невозможные картинки. Невозможный треугольник Пентроуза Невозможный куб Эшера
- 17. Задачи на разрезание и складывание фигур. Пентамино
- 18. Из элементов головоломки складываются
- 19. Треугольник Изучаются виды треугольников, задачи на построение
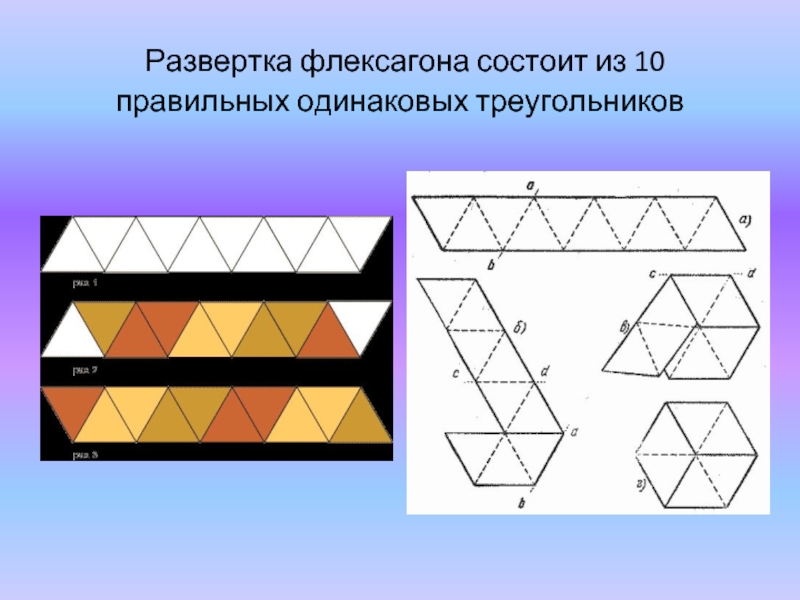
- 20. Развертка флексагона состоит из 10 правильных одинаковых треугольников
- 21. Также изготавливаем модели многогранников Тетраэдр Гексаэдр(куб) Октаэдр
- 22. Знакомство с формулой Л.Эйлера В+Г-Р=2 В-количество вершин, Г-количество граней, Р-количество рёбер выпуклого многогранника.
- 23. Двойственные многогранники Два правильных многогранника называются двойственными,
- 24. Ещё одна головоломка «Танграм», которую дети изготавливают
- 25. Проходим различные единицы длины,
- 26. Топологические опыты Берем 2 бумажных полоски. Склеенная
- 27. Отвечая на вопрос: можно ли нарисовать
- 28. Задача о Кёнигсбергских мостах Леонард Эйлер 1734
Слайд 1Повышение качества математического (геометрического) образования на уроках наглядной геометрии в 5-6
классах.
Часть 1 «5 класс»
Слайд 2 Мир геометрии окружает нас с самого рождения.
Всё,
что мы видим вокруг так или иначе относится к геометрии:
капля воды, загадочный узор снежинки, прямоугольник окна… Ничего не ускользает от внимательного взгляда Геометрии.
капля воды, загадочный узор снежинки, прямоугольник окна… Ничего не ускользает от внимательного взгляда Геометрии.
Слайд 3
Чтобы научить детей внимательно смотреть вокруг, видеть красоту обычных
вещей, делать выводы об увиденном,
в нашей школе
в 5 и 6 классе
1 раз в неделю
ведётся предмет «Наглядная геометрия»
в нашей школе
в 5 и 6 классе
1 раз в неделю
ведётся предмет «Наглядная геометрия»
Слайд 4
Преподавание ведется по пособию для общеобразовательных учреждений «Наглядная геометрия 5-6
классы,
авторы
Игорь Федорович Шарыгин
и Лариса Николаевна Ерганжиева.
Его можно использовать на уроках для обогащения геометрического материала действующих учебников, а также для работы в кружках и факультативах.
авторы
Игорь Федорович Шарыгин
и Лариса Николаевна Ерганжиева.
Его можно использовать на уроках для обогащения геометрического материала действующих учебников, а также для работы в кружках и факультативах.
Слайд 5
Пособие содержит уникальный задачный материал по геометрии,направленный на развитие геометрической интуиции,
пространственного воображения, глазомера, изобразительных навыков.
Основные приёмы решения задач: наблюдение, конструирование, эксперимент.
Основные приёмы решения задач: наблюдение, конструирование, эксперимент.
Слайд 6
На первом занятии мы предлагаем решить ребятам задачу:
Как из
6 одинаковых спичек сложить 4 одинаковых треугольника?
Как правило дети не могут сообразить как решить задачу, потому что привыкли мыслить на листе бумаги…, то есть в плоскости!
Как правило дети не могут сообразить как решить задачу, потому что привыкли мыслить на листе бумаги…, то есть в плоскости!
Слайд 7
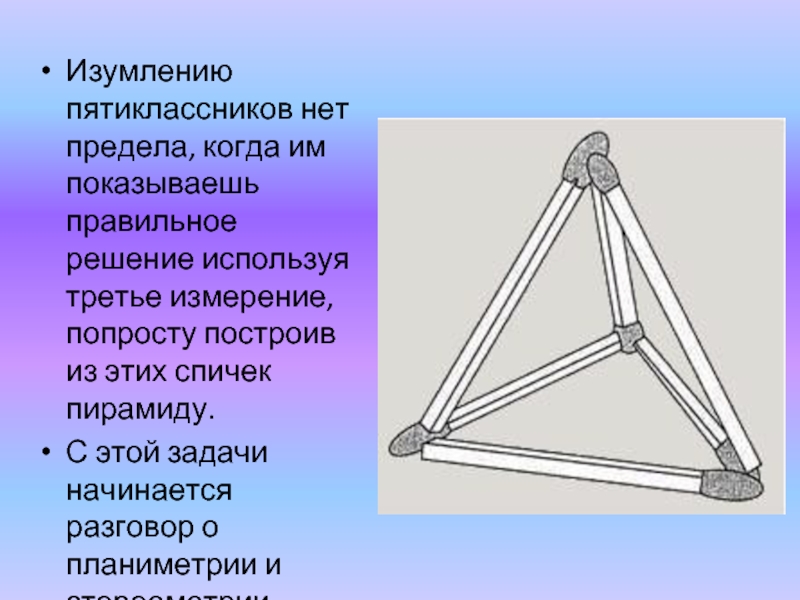
Изумлению пятиклассников нет предела, когда им показываешь правильное решение используя третье
измерение, попросту построив из этих спичек пирамиду.
С этой задачи начинается разговор о планиметрии и стереометрии.
С этой задачи начинается разговор о планиметрии и стереометрии.
Слайд 8Закономерна следующая тема:
«Пространство и размерность»
Ребята знакомятся с
0-мерным (точка),
1-мерным
(прямая),
2-мерным (плоскость),
3-мерным пространствами.
Знакомятся с геометрическими жителями каждого из них.
2-мерным (плоскость),
3-мерным пространствами.
Знакомятся с геометрическими жителями каждого из них.
Затем они сами ассоциируют услышанное с современным телевидением 2-Д, 3-Д
Начинают фантазировать о 4-Д, 5-Д,…
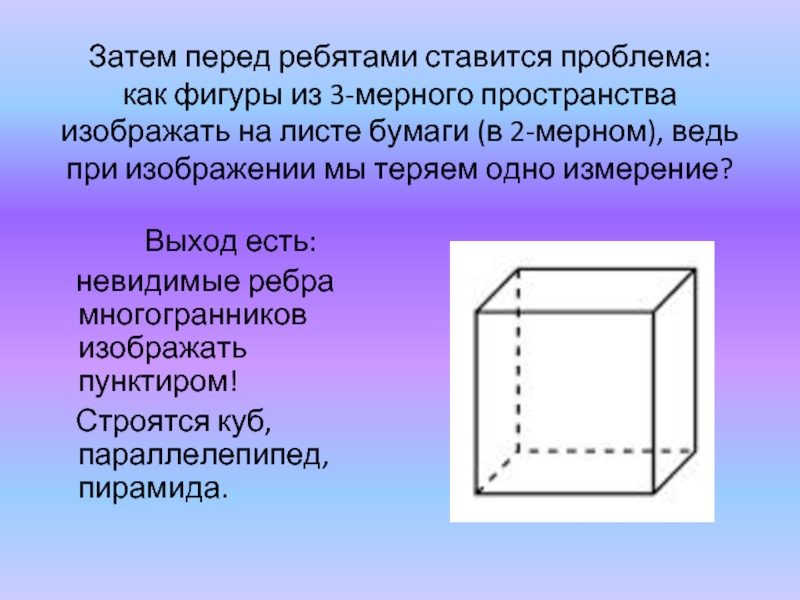
Слайд 9Затем перед ребятами ставится проблема:
как фигуры из 3-мерного пространства изображать на листе бумаги (в 2-мерном), ведь при изображении мы теряем одно измерение?
Выход есть:
невидимые ребра многогранников изображать пунктиром!
Строятся куб, параллелепипед, пирамида.
Слайд 10Перспектива
Картинка венгерского художника Виктора Вазарели
«Изучение перспективы»
Линии, уходящие вглубь, сходятся в одной точке, а фигура, находящаяся дальше от нас, изображается в виде формы меньших размеров.
Слайд 11Перспектива и иллюзии
Помогает с помощью изгибов линий передать вмятины, выпуклости, капли
на плоском листе бумаги.
Игра цветов заставляет на листе бумаги крутиться круги или двигаться волны.
Игра цветов заставляет на листе бумаги крутиться круги или двигаться волны.
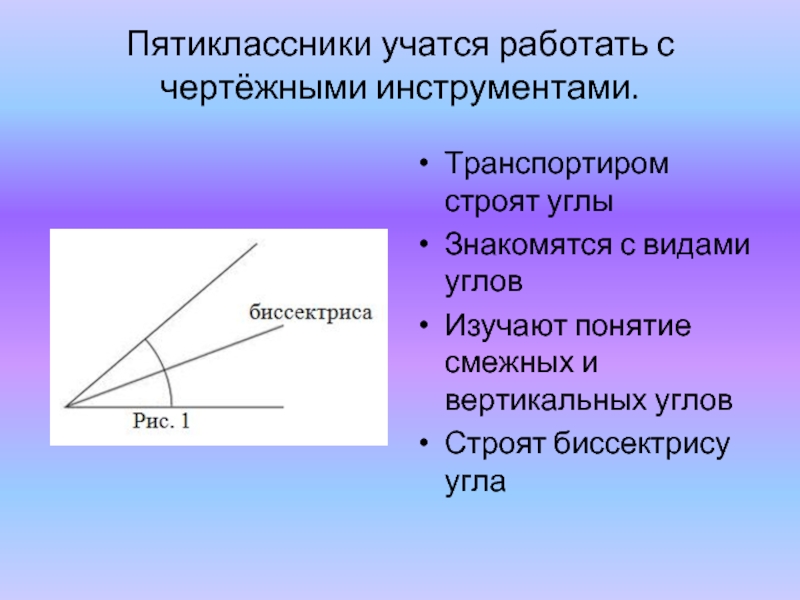
Слайд 12Пятиклассники учатся работать с чертёжными инструментами.
Транспортиром строят углы
Знакомятся с видами углов
Изучают
понятие смежных и вертикальных углов
Строят биссектрису угла
Строят биссектрису угла
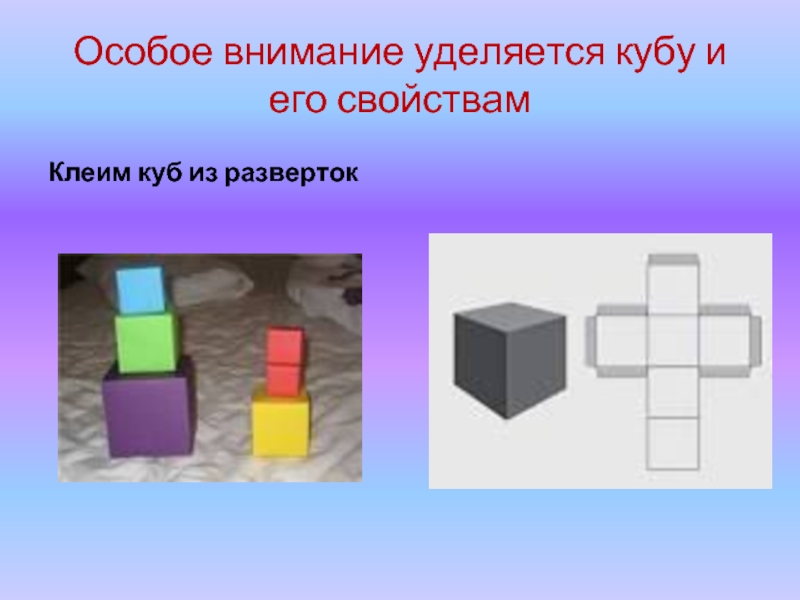
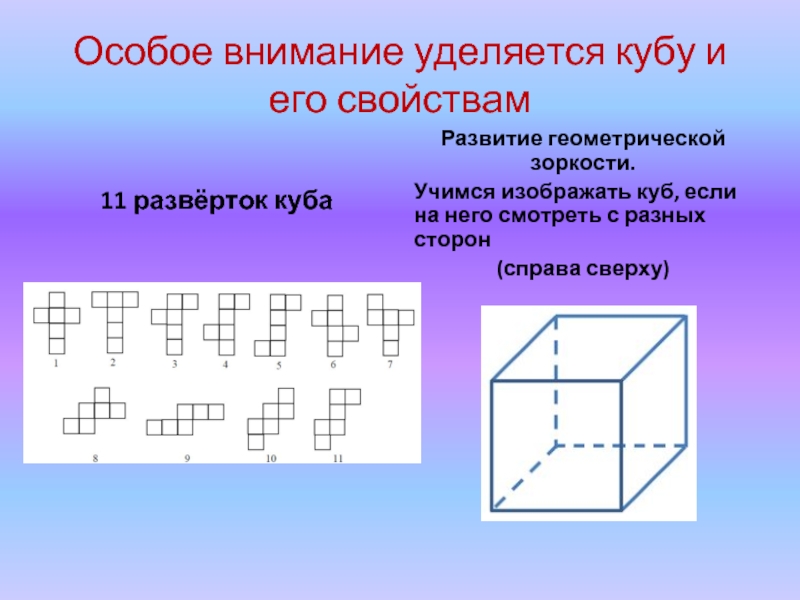
Слайд 14Особое внимание уделяется кубу и его свойствам
11 развёрток куба
Развитие геометрической зоркости.
Учимся
изображать куб, если на него смотреть с разных сторон
(справа сверху)
(справа сверху)
Слайд 15Помогают развивать геометрическую зоркость
рисунки с неоднозначными фигурами.
Что изображено?
Фигура Маха
Леди и
старуха
Слайд 16Помогают развивать геометрическую зоркость
невозможные картинки.
Невозможный треугольник Пентроуза
Невозможный куб Эшера
Слайд 17Задачи на разрезание и складывание фигур. Пентамино – это популярная логическая головоломка
для детей и взрослых. Игра состоит из 12 плоских фигур. Все фигуры состоят из 5 квадратов. Каждый элемент обозначает латинскую букву, форму которой он напоминает.
Слайд 18
Из элементов головоломки складываются буквы, прямоугольники, цифры, животные.
Пентамино
развивает абстрактное мышление, воображение, воспитывает настойчивость и терпение, учит определять, создавать, анализировать.
В пентамино фантазия может творить чудеса: из непонятных разной формы фигур может возникнуть фигура собаки, машины, дерева.
В пентамино фантазия может творить чудеса: из непонятных разной формы фигур может возникнуть фигура собаки, машины, дерева.
Слайд 19Треугольник
Изучаются виды треугольников, задачи на построение треугольников по 3 элементам
Флексагон
(изготовление игрушки)
Эта игрушка (от англ. to flex, что означает «складываться, гнуться») Другими словами, флексагон — гнущийся многоугольник.
Флексагон обладает удивительной способностью внезапно менять свою форму и цвет.
Флексагон обладает удивительной способностью внезапно менять свою форму и цвет.
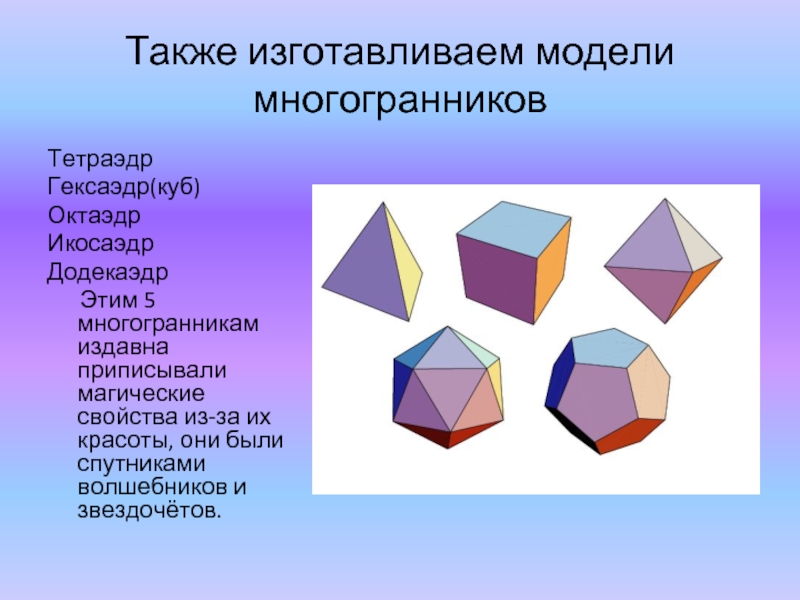
Слайд 21Также изготавливаем модели многогранников
Тетраэдр
Гексаэдр(куб)
Октаэдр
Икосаэдр
Додекаэдр
Этим 5 многогранникам издавна приписывали
магические свойства из-за их красоты, они были спутниками волшебников и звездочётов.
Слайд 22Знакомство с формулой Л.Эйлера
В+Г-Р=2
В-количество вершин,
Г-количество граней,
Р-количество рёбер
выпуклого многогранника.
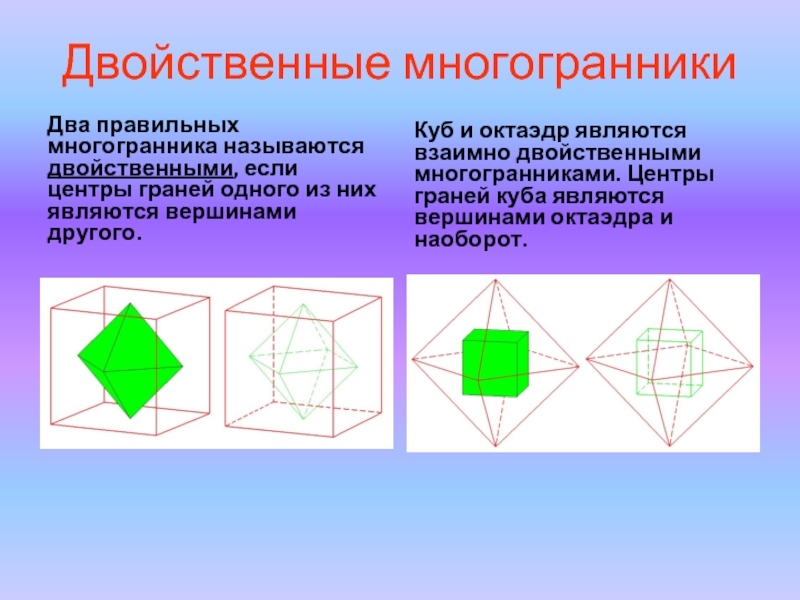
Слайд 23Двойственные многогранники
Два правильных многогранника называются двойственными, если центры граней одного из
них являются вершинами другого.
Куб и октаэдр являются взаимно двойственными многогранниками. Центры граней куба являются вершинами октаэдра и наоборот.
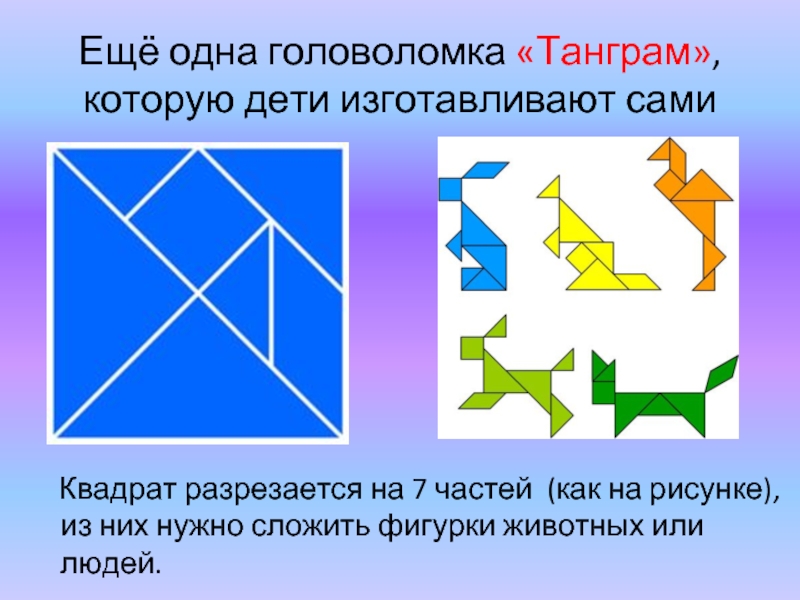
Слайд 24Ещё одна головоломка «Танграм», которую дети изготавливают сами
Квадрат разрезается
на 7 частей (как на рисунке), из них нужно сложить фигурки животных или людей.
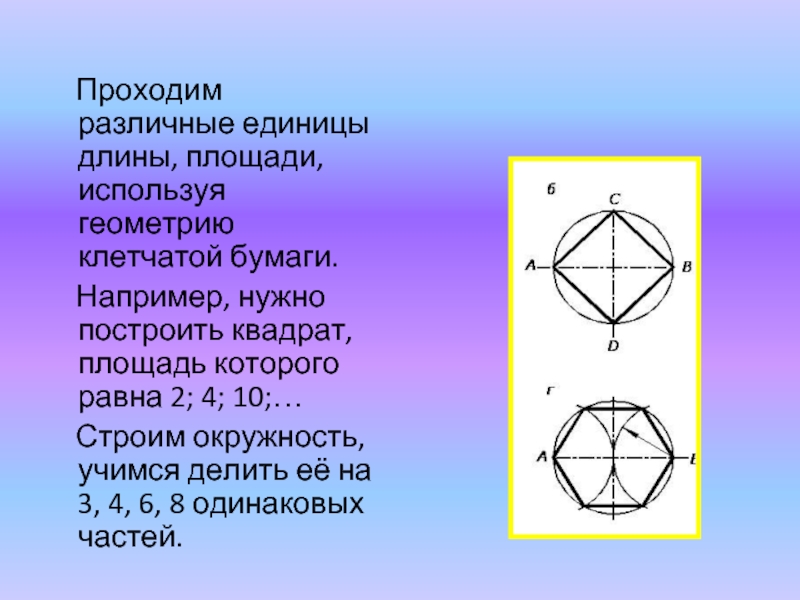
Слайд 25
Проходим различные единицы длины, площади, используя геометрию клетчатой бумаги.
Например, нужно построить квадрат, площадь которого равна 2; 4; 10;…
Строим окружность, учимся делить её на 3, 4, 6, 8 одинаковых частей.
Строим окружность, учимся делить её на 3, 4, 6, 8 одинаковых частей.
Слайд 26Топологические опыты
Берем 2 бумажных полоски.
Склеенная в кольцо полоска имеет внутреннюю и
внешнюю стороны и два края. Жук может совершить "кругосветное путешествие" по кольцу, оставаясь либо на внутренней, либо на внешней стороне.
Вторую полоску перекручиваем в пол-оборота и склеиваем концы.
Получаем Лист Мёбиуса, у него есть только одна сторона – это односторонняя поверхность с одним краем.
Жук, ползущий по середине листа Мебиуса (не пересекая края), вернется в исходную точку в положении "вверх ногами".
При разрезании листа Мебиуса по средней линии он не распадается на две части.
Слайд 27Отвечая на вопрос: можно ли нарисовать фигуру одним росчерком, не отрывая
карандаш от бумаги и не проходя по одной линии дважды?
-приходим к понятию графа.
Учимся определять четность узлов графа.
Если граф связный, то обойти его можно, если нечётных узлов у него 0 или 2.
Если 2, то маршрут начинается в одной из них, а заканчивается в другой
Если 0,то маршрут начинается в любой вершине и в ней же заканчиватся.
Слайд 28Задача о Кёнигсбергских мостах
Леонард Эйлер 1734 год
Можно ли, гуляя по городу
пройти все 7 мостов реки Прегель, но каждый только по одному разу?
Эйлер доказал невозможность такого обхода, явившись основателем теории графов.
