- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
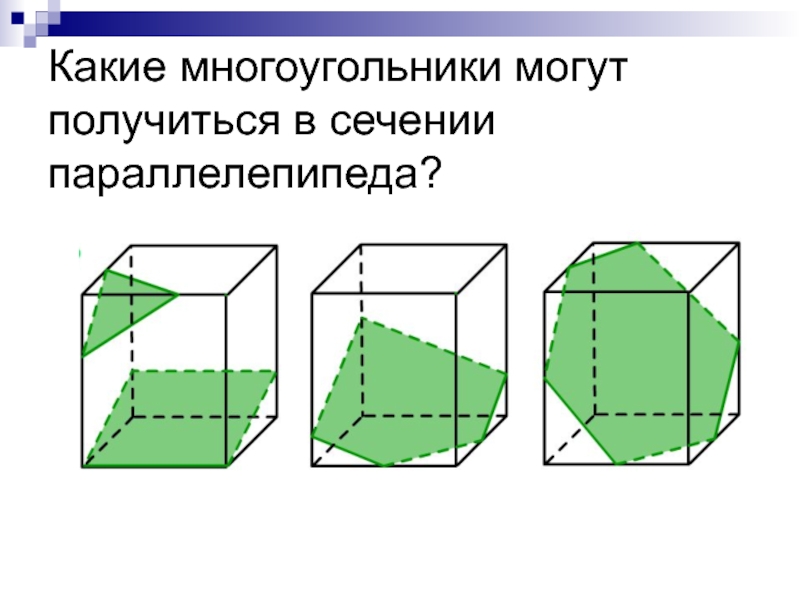
Построение сечений параллелепипеда презентация
Содержание
Слайд 4
A
B
С
B1
D1
D
K
M
C1
A1
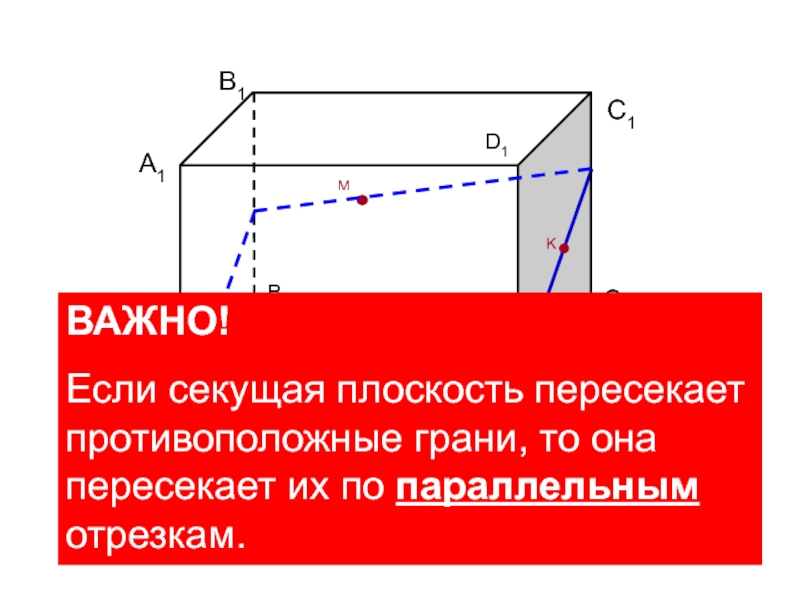
ВАЖНО!
Если секущая плоскость пересекает противоположные грани, то она пересекает их по
параллельным отрезкам.
Слайд 6
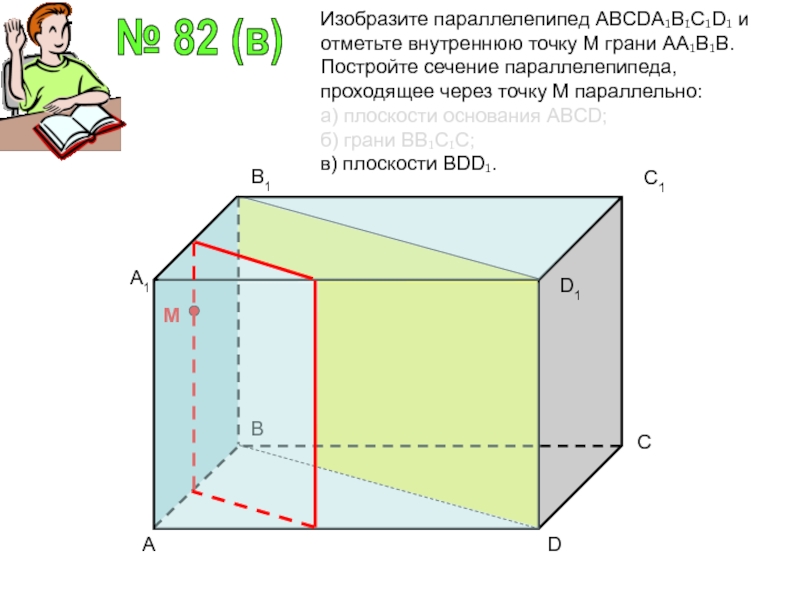
№ 82 (в)
A
B
C1
D
A1
B1
D1
C
M
Изобразите параллелепипед ABCDA₁B₁C₁D₁ и отметьте внутреннюю точку М грани
АА₁В₁В. Постройте сечение параллелепипеда, проходящее через точку М параллельно:
а) плоскости основания ABCD;
б) грани ВВ₁С₁С;
в) плоскости BDD₁.
а) плоскости основания ABCD;
б) грани ВВ₁С₁С;
в) плоскости BDD₁.
Слайд 7
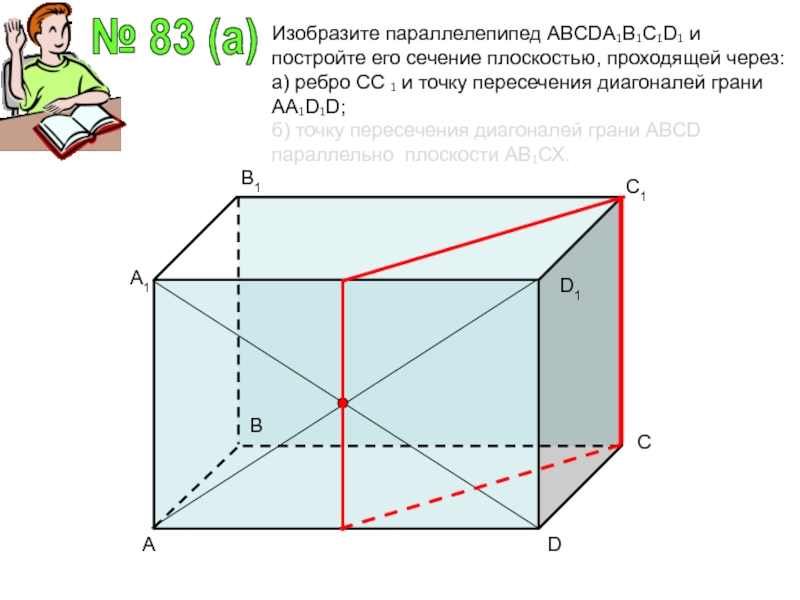
№ 83 (a)
Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей
через:
а) ребро СС ₁ и точку пересечения диагоналей грани AA₁D₁D;
б) точку пересечения диагоналей грани ABCD параллельно плоскости АВ₁СХ.
а) ребро СС ₁ и точку пересечения диагоналей грани AA₁D₁D;
б) точку пересечения диагоналей грани ABCD параллельно плоскости АВ₁СХ.
A
C1
D
A1
B1
D1
C
B
Слайд 8
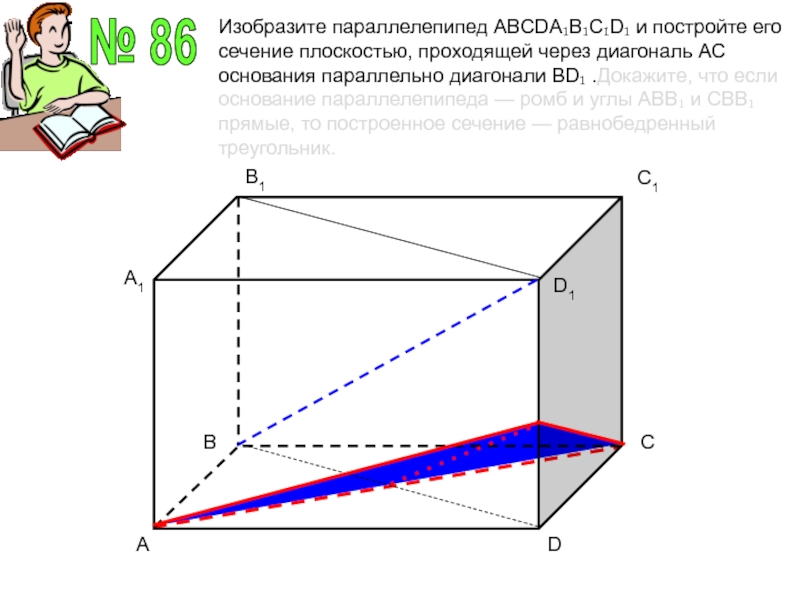
№ 86
A
C1
D
A1
B1
D1
B
C
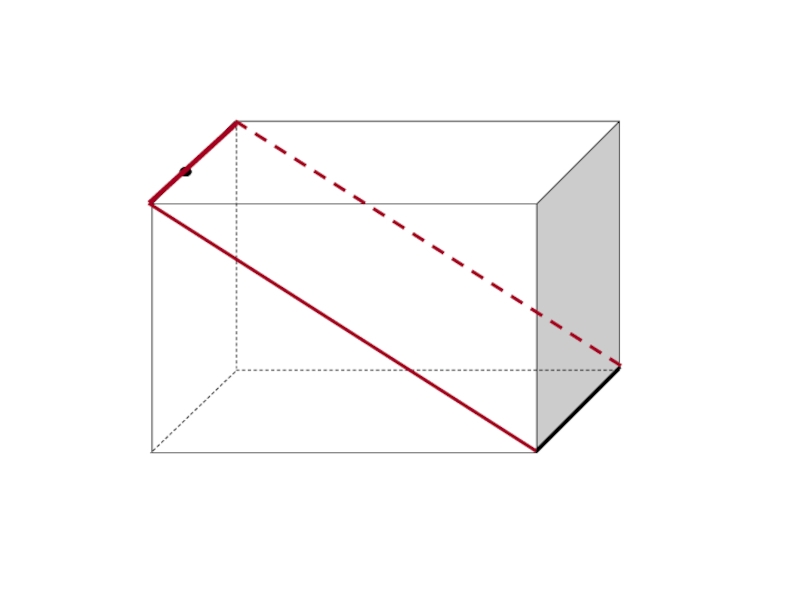
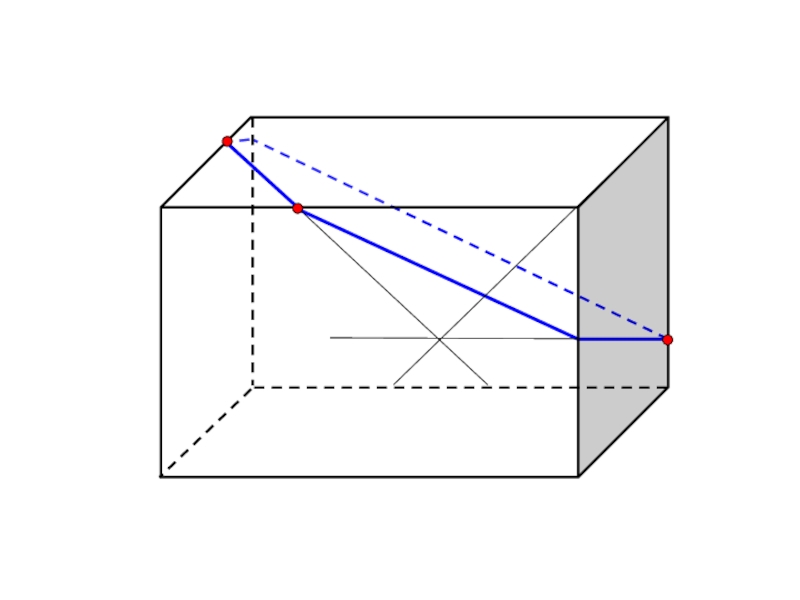
Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей через
диагональ АС основания параллельно диагонали BD₁ .Докажите, что если основание параллелепипеда — ромб и углы АВВ₁ и СВВ₁ прямые, то построенное сечение — равнобедренный треугольник.
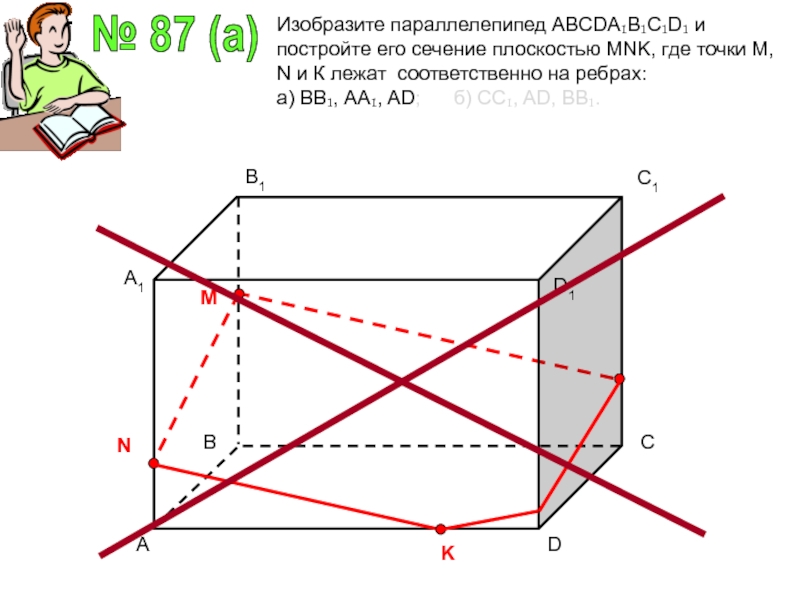
Слайд 9№ 87 (a)
A
C1
D
A1
B1
D1
B
C
M
N
K
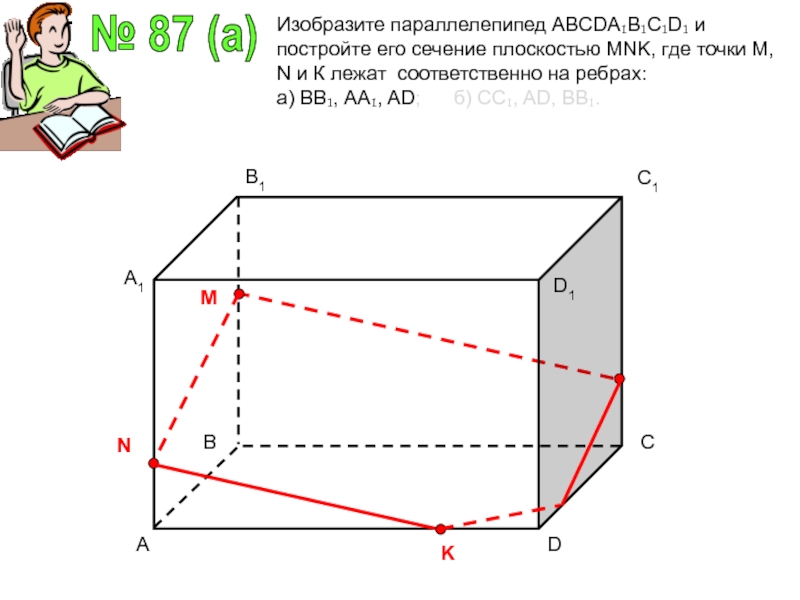
Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью MNK,
где точки М, N и К лежат соответственно на ребрах:
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.
Слайд 10№ 87 (a)
A
C1
D
A1
B1
D1
B
C
M
N
K
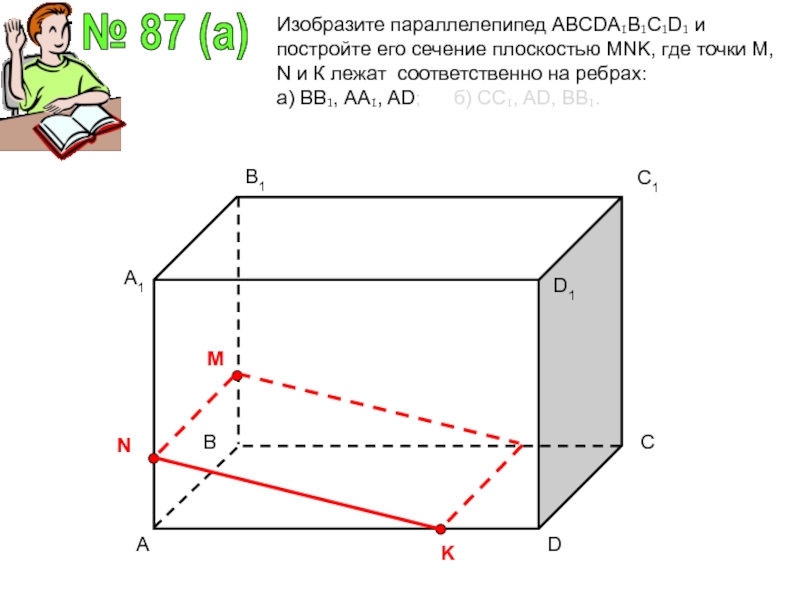
Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью MNK,
где точки М, N и К лежат соответственно на ребрах:
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.
Слайд 11№ 87 (a)
A
C1
D
A1
B1
D1
B
C
M
N
K
Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью MNK,
где точки М, N и К лежат соответственно на ребрах:
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.
Слайд 12№ 87 (a)
A
C1
D
A1
B1
D1
B
C
M
N
K
Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью MNK,
где точки М, N и К лежат соответственно на ребрах:
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.
а) ВВ₁, АА₁, AD; б) СС₁, AD, ВВ₁.