- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Постоянный электрический ток презентация
Содержание
- 1. Постоянный электрический ток
- 2. Условия существования электрического тока Электрический ток –
- 3. Характеристики тока Количественной мерой тока служит сила
- 4. Электрический ток может быть распределен по
- 5. Если обозначить через
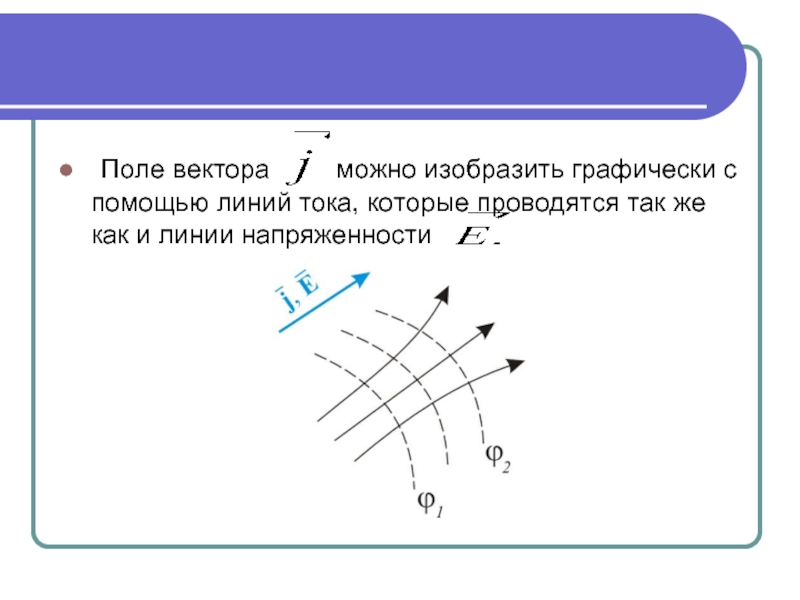
- 6. Поле вектора
- 7. Уравнение непрерывности Представим себе в некоторой проводящей
- 8. Т.е. Данное
- 9. Преобразуем уравнение
- 10. Стянув поверхность в точку, получим
- 11. Уравнение означает,
- 12. Закон Ома в дифференциальной форме Установим связь
- 13. Соотношение
- 14. Закон Ома для неоднородного участка цепи
- 15. Закон Ома в случае действия полей
- 16. В случае постоянного тока
- 17. Классическая теория электропроводности металлов. Теория Друде. Друде
- 18. Распространяя на электроны результаты кинетической теории
- 19. Найдем вызываемое полем изменение среднего
- 20. Закон Ома в дифференциальной форме За время
- 21. Среднее значение скорости
- 22. Если бы электроны не сталкивались с
- 23. Закон Джоуля-Ленца Скорость электрона равна сумме скоростей
- 24. Средняя кинетическая энергия электрона
- 25. Каждый электрон претерпевает в секунду
- 26. Затруднения классической теории электропроводности металлов 1. Из
- 27. 2. Согласно классической теории электронный газ
Слайд 1Постоянный электрический ток
Условия возникновения тока
Характеристики тока
Уравнение непрерывности
Теория Друде
Слайд 2Условия существования электрического тока
Электрический ток – это упорядоченное движение носителей заряда.
Для
наличие зарядов, способных перемещаться в пределах тела;
в проводнике должно существовать электрическое поле.
Слайд 3Характеристики тока
Количественной мерой тока служит сила тока - заряд, перенесенный через
За направление тока принято направление движения положительных зарядов.
Слайд 4
Электрический ток может быть распределен по сечению проводника неравномерно. Поэтому для
Модуль плотности тока численно равен заряду, переносимому через единичную площадку, расположенную в данной точке перпендикулярно направлению движения носителей, за единицу времени
Слайд 5
Если обозначить через скорость упорядоченного движения зарядов, то
Плотность тока и сила тока связаны соотношением
Слайд 6
Поле вектора можно изобразить графически с
Слайд 7Уравнение непрерывности
Представим себе в некоторой проводящей среде, где течет ток, замкнутую
дает заряд, выходящий за единицу времени наружу из объема , охваченного поверхностью
Из закона сохранения заряда следует, что этот интеграл равен убыли заряда в единицу времени внутри объема
Слайд 8
Т.е.
Данное равенство называется уравнением непрерывности.
В случае стационарного
так как
Слайд 10
Стянув поверхность в точку, получим
Для постоянного тока
Слайд 11
Уравнение
означает, что в случае постоянного тока поле
Слайд 12Закон Ома в дифференциальной форме
Установим связь между плотностью тока и напряженностью
Воспользуемся законом Ома
для участка цепи
Слайд 14Закон Ома для неоднородного участка цепи
Для поддержания тока в цепи
Слайд 15
Закон Ома в случае действия полей
запишется в виде
Это обобщенный закон Ома.
Выполним преобразования
Слайд 16
В случае постоянного тока
Приходим к интегральной форме закона Ома
Слайд 17Классическая теория электропроводности металлов. Теория Друде.
Друде предположил, что электроны в металле
Слайд 18
Распространяя на электроны результаты кинетической теории газов, можно оценить среднюю скорость
При включении поля на тепловое движение накладывается упорядоченное движение электронов с некоторой скоростью
Так как то
Слайд 19
Найдем вызываемое полем изменение среднего
значения кинетической энергии электронов
Избыточная энергия
по предположению Друде передается при
соударении решетке, и скорость упорядоченного
движения электрона обращается в ноль.
Слайд 20Закон Ома в дифференциальной форме
За время свободного пробега
ускоренный внешним однородным электрическим полем, приобретает скорость
Слайд 21
Среднее значение скорости при равноускоренном движении равно половине максимальной
Для плотности тока
Закон Ома в дифференциальной форме
Слайд 22
Если бы электроны не сталкивались с узлами решетки, то длина свободного
Таким образом сопротивление металлов обусловлено соударением свободных электронов с ионами решетки.
Слайд 23Закон Джоуля-Ленца
Скорость электрона равна сумме скоростей теплового движения
Слайд 24
Средняя кинетическая энергия электрона содержит дополнительное слагаемое, обусловленное полем
Столкнувшись
Слайд 25
Каждый электрон претерпевает в секунду
единицу времени будет выделяться количество теплоты
Закон Джоуля-Ленца в дифференциальной форме
Слайд 26Затруднения классической теории электропроводности металлов
1. Из формулы
, так как
На самом деле
Слайд 27
2. Согласно классической теории электронный газ должен обладать молярной теплоемкостью
На самом деле она равна Наличие электронов не сказывается на теплоемкости, что может быть объяснено только с точки зрения квантовой механики.