- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка учащихсяк ЕГЭ по математике презентация
Содержание
- 1. Подготовка учащихсяк ЕГЭ по математике
- 2. Основная проблема: Совместить прохождение программы с подготовкой учащихся к ЕГЭ
- 3. Пути решения проблемы Выделение времени на подготовку
- 4. Задания группы С1 Классификация заданий по алгоритмам
- 5. Задания группы С1 Классификация заданий по алгоритмам
- 6. Пути решения проблемы Выделение времени на подготовку
- 7. Универсальный способ решения – способ, с
- 8. Задания группы С2: Универсальный способ решения
- 9. Задания группы С2: Универсальный способ решения
- 10. Задания группы С2: Универсальный способ решения
- 14. Пути решения проблемы Выделение времени на подготовку
- 15. Вовлечение в процесс решения как можно большего количества учащихся
- 16. Спасибо за внимание!
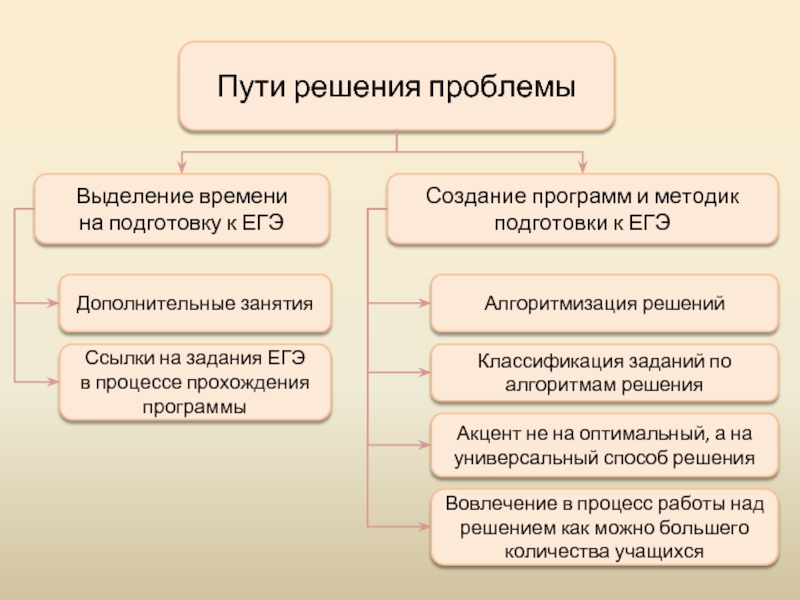
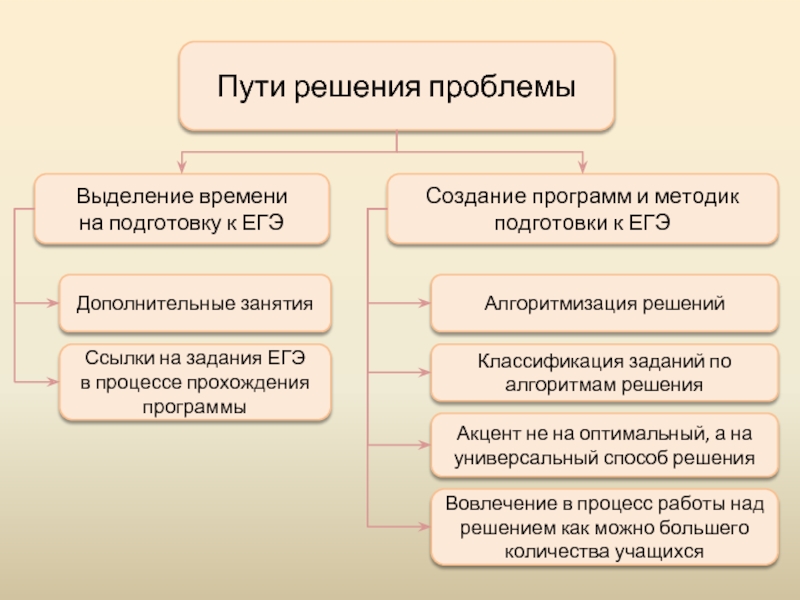
Слайд 3Пути решения проблемы
Выделение времени
на подготовку к ЕГЭ
Создание программ и методик подготовки
Дополнительные занятия
Ссылки на задания ЕГЭ
в процессе прохождения программы
Алгоритмизация решений
Классификация заданий по алгоритмам решения
Акцент не на оптимальный, а на универсальный способ решения
Вовлечение в процесс работы над решением как можно большего количества учащихся
Слайд 4Задания
группы С1
Классификация заданий
по алгоритмам решения
Тип 1
, где A и B –
Решение:
Примеры:
Слайд 5Задания
группы С1
Классификация заданий
по алгоритмам решения
Тип 2
, где A и B –
Решение:
Примеры:
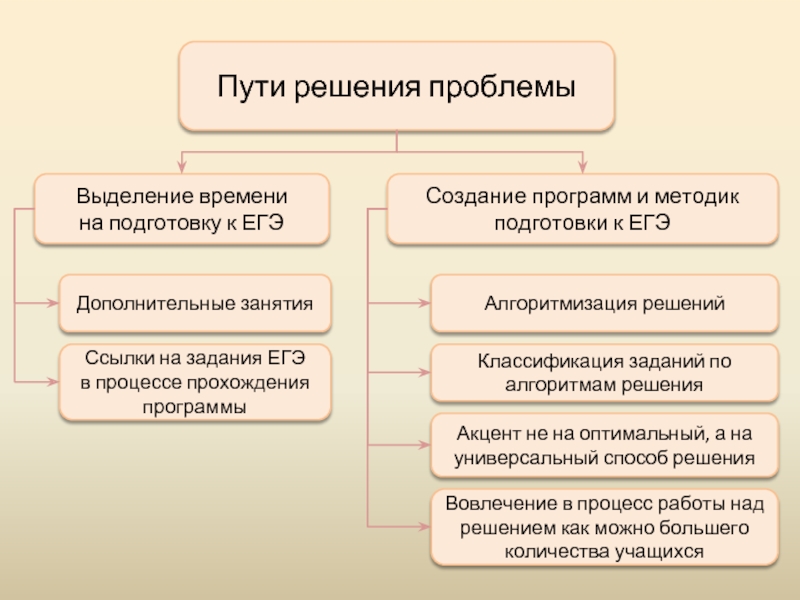
Слайд 6Пути решения проблемы
Выделение времени
на подготовку к ЕГЭ
Создание программ и методик подготовки
Дополнительные занятия
Ссылки на задания ЕГЭ
в процессе прохождения программы
Алгоритмизация решений
Классификация заданий по алгоритмам решения
Акцент не на оптимальный, а на универсальный способ решения
Вовлечение в процесс работы над решением как можно большего количества учащихся
Слайд 7Универсальный способ решения –
способ, с помощью которого можно решить как
Слайд 8Задания группы С2:
Универсальный способ решения
Метод координат
Преимущества метода:
80% заданий данной группы можно
У учащихся появляется возможность избежать ошибки, связанной с построением
Метод имеет очень отлаженный алгоритм решения: решение всех задач сводится к одной формуле
✓
✓
✓
Слайд 9Задания группы С2:
Универсальный способ решения
Метод координат
Этапы решения задачи:
Введение прямоугольной системы координат
Задание
Нахождение координат начала и конца заданных векторов и координат самих векторов
1)
2)
3)
Нахождение косинуса угла между прямыми или синуса угла между прямой и плоскостью по известной формуле
4)
Слайд 10Задания группы С2:
Универсальный способ решения
Метод координат
Для успешной работы методом координат:
Отработка введения
Отработка нахождения координат искомых точек многогранника
Нахождение углов между прямыми, прямой и плоскостью и двумя плоскостями
✓
✓
✓
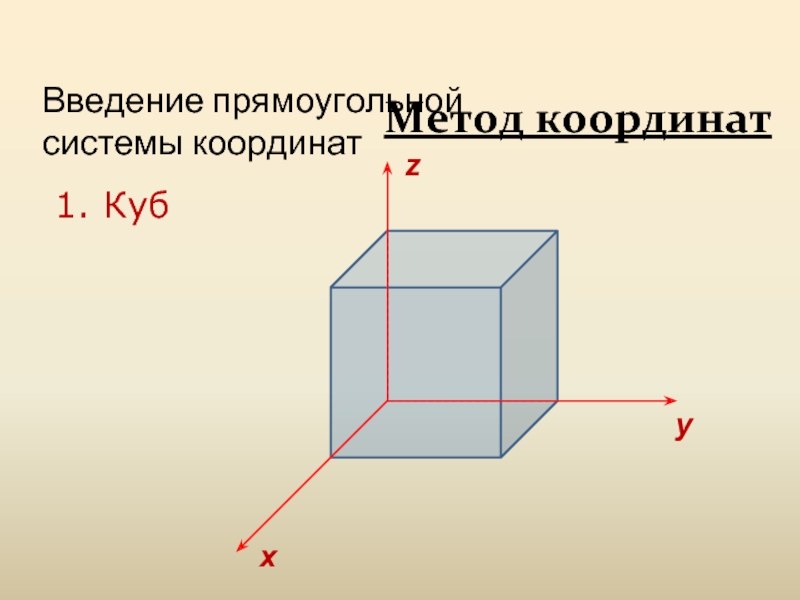
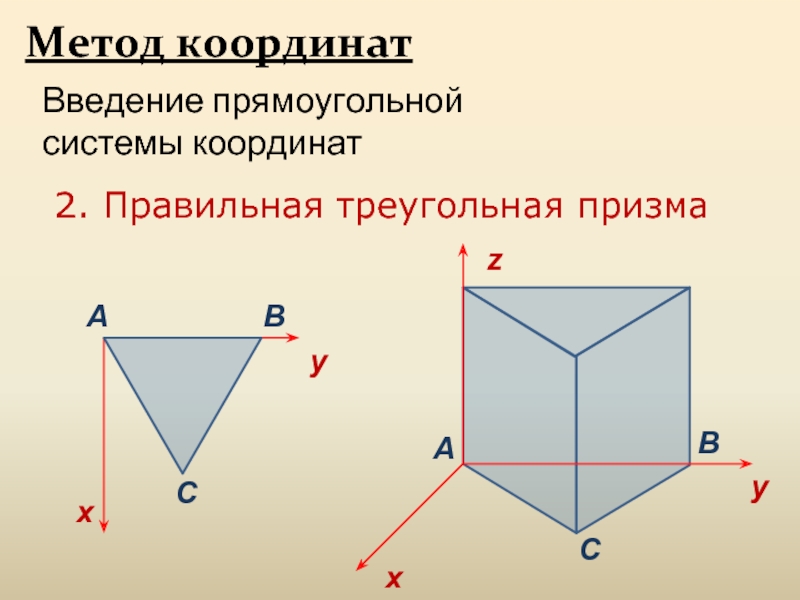
Слайд 12
Метод координат
Введение прямоугольной системы координат
2. Правильная треугольная призма
x
z
y
x
y
A
B
C
A
B
C
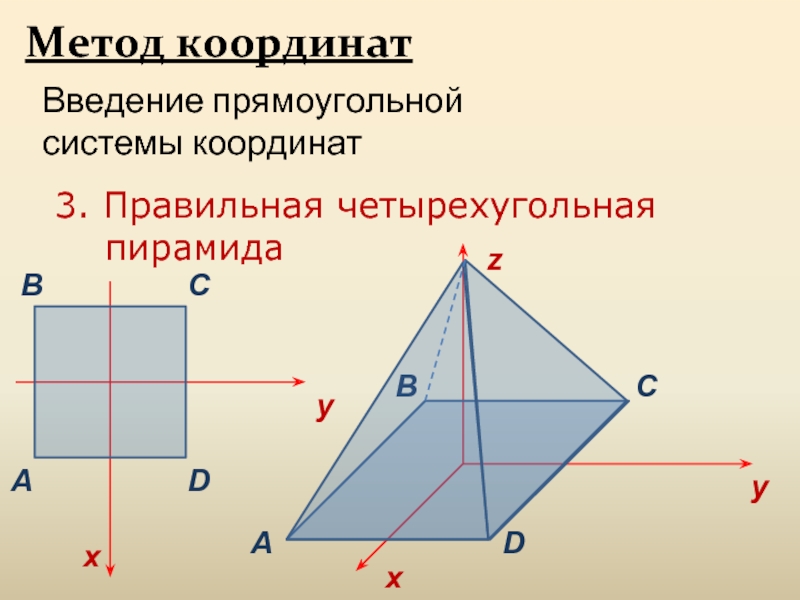
Слайд 13
Метод координат
Введение прямоугольной системы координат
3. Правильная четырехугольная
пирамида
x
z
y
x
y
A
B
C
A
B
C
D
D
Слайд 14Пути решения проблемы
Выделение времени
на подготовку к ЕГЭ
Создание программ и методик подготовки
Дополнительные занятия
Ссылки на задания ЕГЭ
в процессе прохождения программы
Алгоритмизация решений
Классификация заданий по алгоритмам решения
Акцент не на оптимальный, а на универсальный способ решения
Вовлечение в процесс работы над решением как можно большего количества учащихся