- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площадь трапеции?Это интересно! презентация
Содержание
- 1. Площадь трапеции?Это интересно!
- 2. Основными целями моей работы были: Сформулировать основные
- 3. Основная формула площади трапеции была выведена девятью
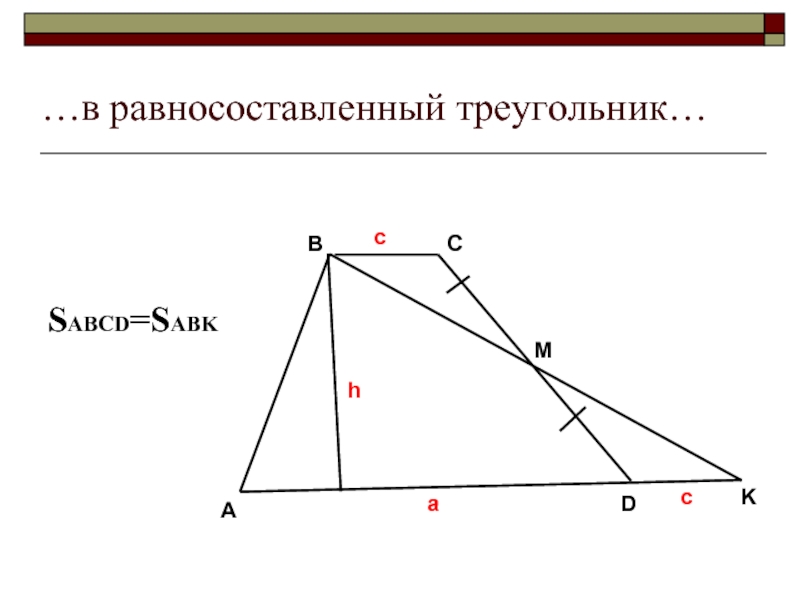
- 4. …в равносоставленный треугольник… SABCD=SABK
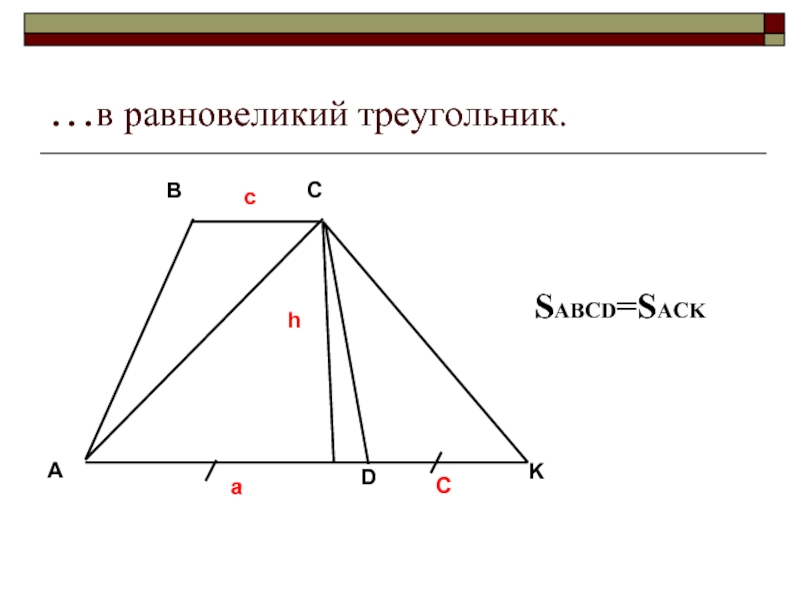
- 5. …в равновеликий треугольник. SABCD=SACK
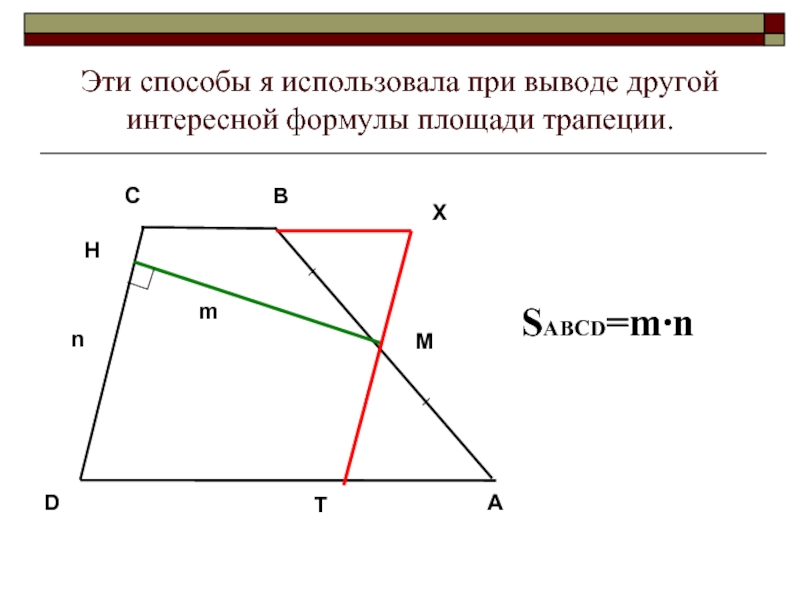
- 6. SABCD=m∙n Эти способы я использовала при выводе другой интересной формулы площади трапеции.
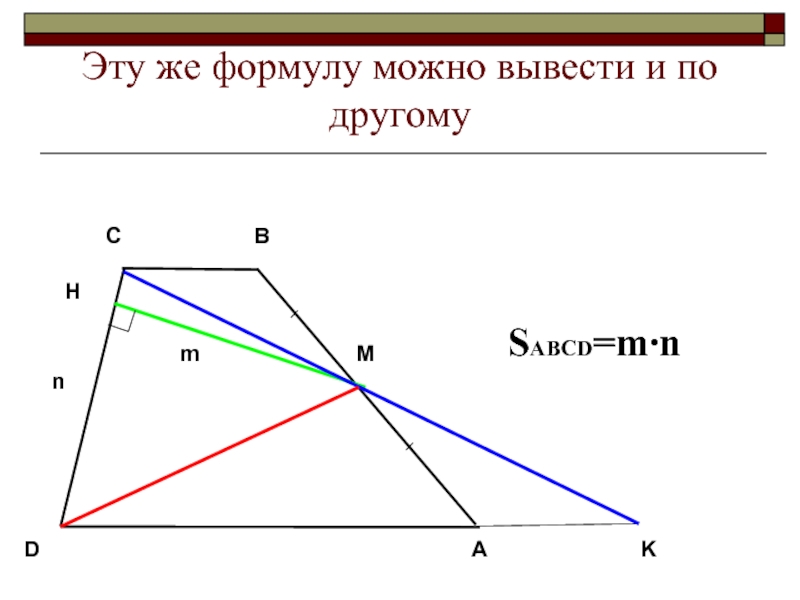
- 7. SABCD=m∙n Эту же формулу можно вывести и по другому
- 8. С помощью формулы Герона была получена такая формула площади трапеции:
- 9. Причем, если треугольник АСК – прямоугольный (АС
- 10. Исследования показали, что если квадрат суммы
- 11. Также доказана и справедливость утверждения: Если 4m22=d12+d22,
- 12. Он был использован при получении другой формулы
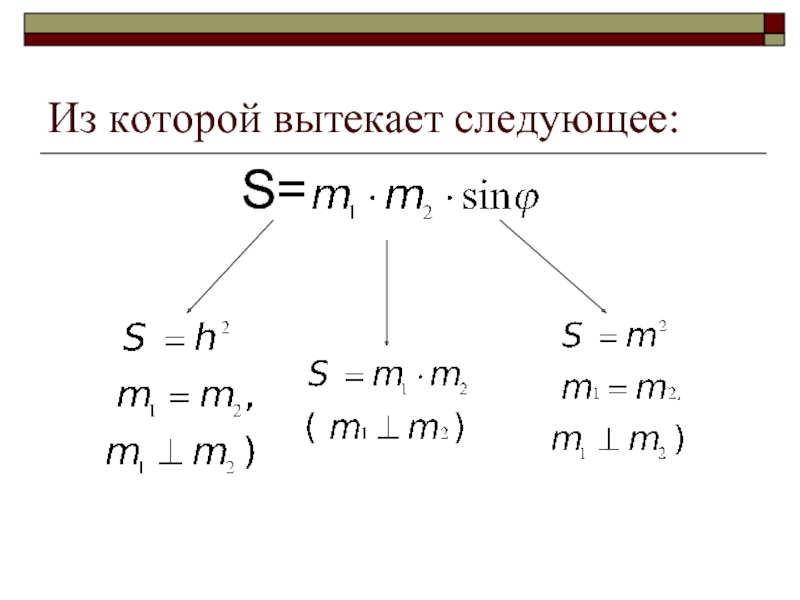
- 14. Из которой вытекает следующее:
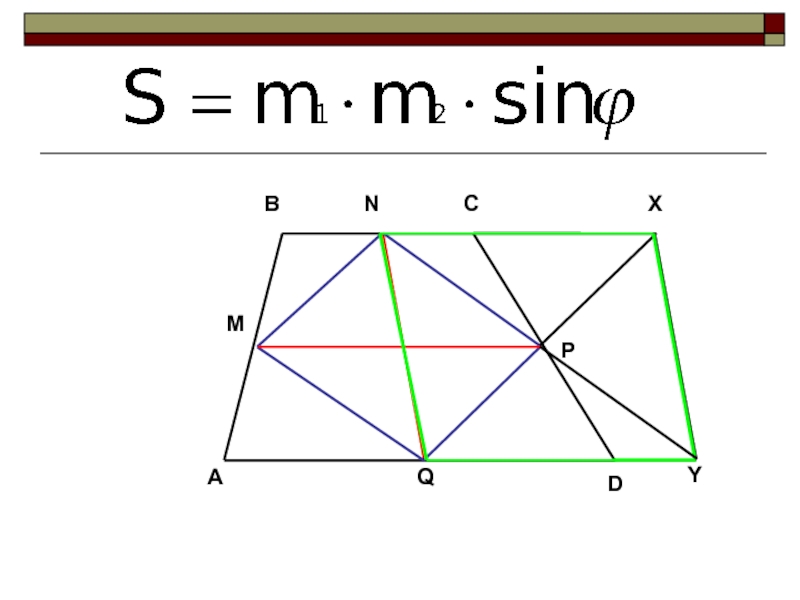
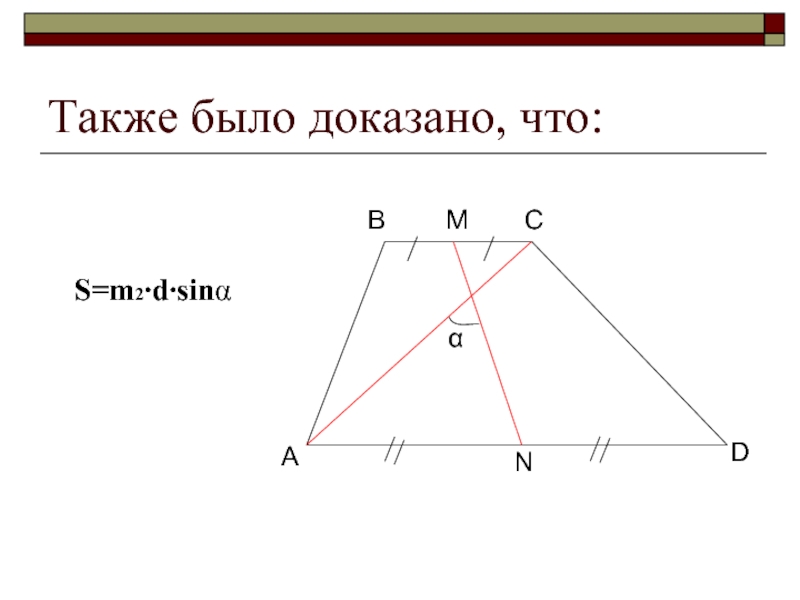
- 15. Также было доказано, что: S=m2∙d∙sinα
- 16. S=m1∙d∙sinβ S=m1∙d∙sinβ
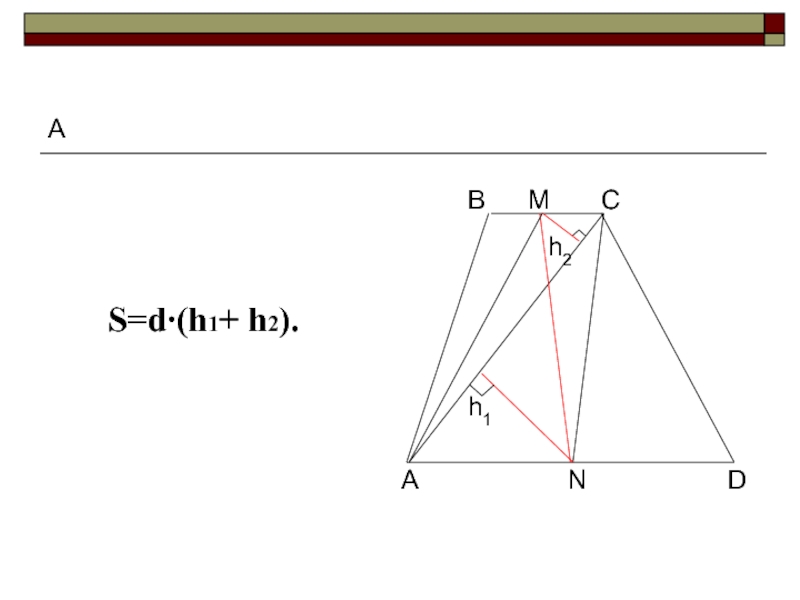
- 17. A S=d∙(h1+ h2).
- 18. И опять, если d1┴d2, то S=0,5∙d1∙d2 (ведь sin90º=1). В работе было доказано, что:
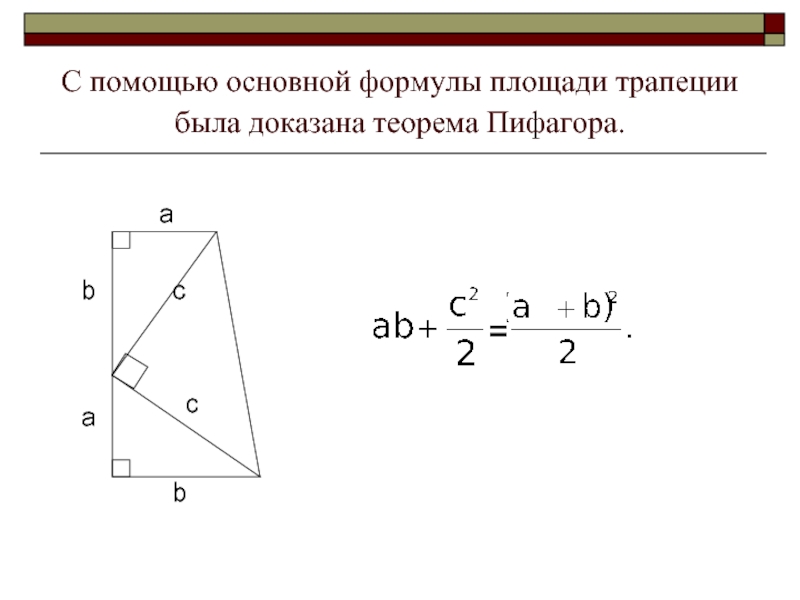
- 19. С помощью основной формулы площади трапеции была доказана теорема Пифагора.
- 20. Выводы В данной исследовательской работе разными способами
Основными целями моей работы были: Сформулировать основные свойства площадей многоугольников, понятия равносоставленности и равновеликости многоугольников, метода разложения (или разбиения), как способа вычисления площадей. Познакомиться с историческими сведениями о возникновении потребности человека
Слайд 2Основными целями моей работы были:
Сформулировать основные свойства площадей многоугольников, понятия равносоставленности
и равновеликости многоугольников, метода разложения (или разбиения), как способа вычисления площадей.
Познакомиться с историческими сведениями о возникновении потребности человека в делении площадей и преобразованиях равновеликих многоугольников.
Используя метод площадей, вывести разными способами основную формулу площади трапеции, продемонстрировав ее применение к доказательству теоремы Пифагора.
Доказать справедливость других формул площади трапеции.
Познакомиться с историческими сведениями о возникновении потребности человека в делении площадей и преобразованиях равновеликих многоугольников.
Используя метод площадей, вывести разными способами основную формулу площади трапеции, продемонстрировав ее применение к доказательству теоремы Пифагора.
Доказать справедливость других формул площади трапеции.
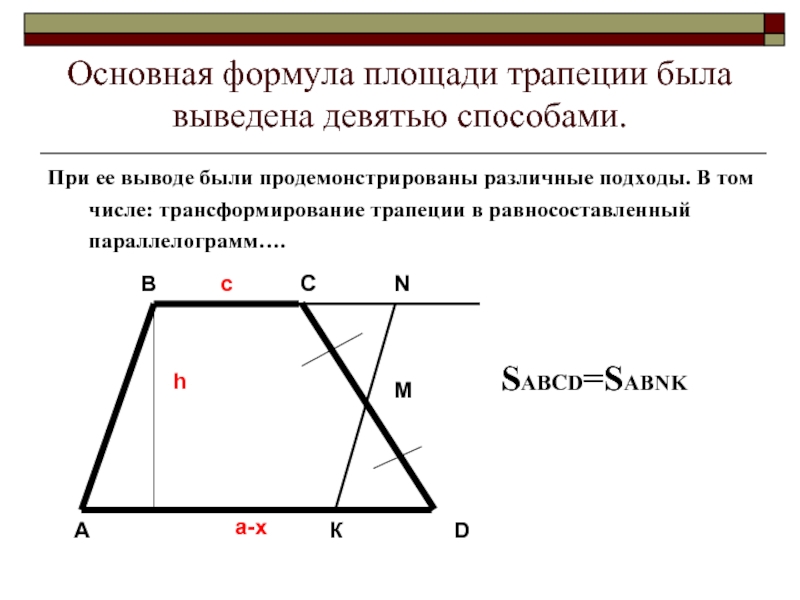
Слайд 3Основная формула площади трапеции была выведена девятью способами.
При ее выводе были
продемонстрированы различные подходы. В том числе: трансформирование трапеции в равносоставленный параллелограмм….
SABCD=SABNK
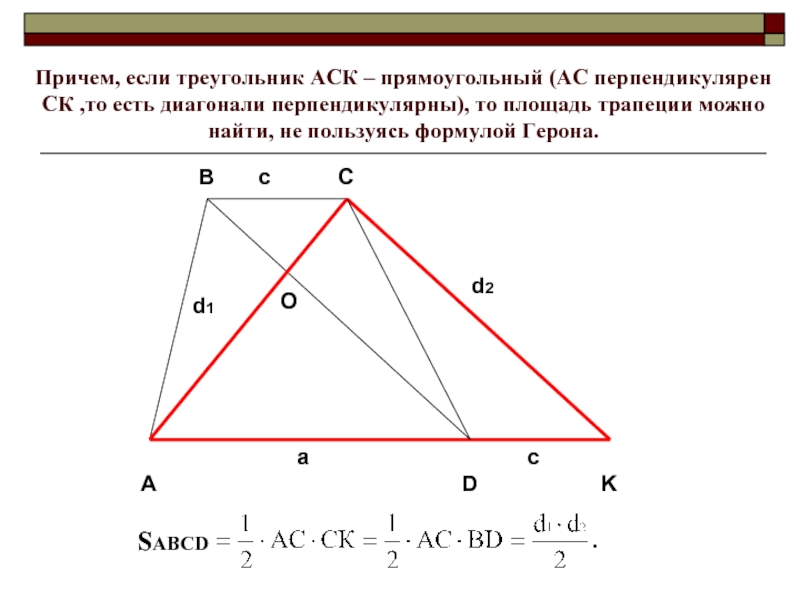
Слайд 9Причем, если треугольник АСК – прямоугольный (АС перпендикулярен СК ,то есть
диагонали перпендикулярны), то площадь трапеции можно найти, не пользуясь формулой Герона.
Слайд 10
Исследования показали, что если квадрат суммы оснований трапеции равен сумме квадратов
ее диагоналей, то диагонали трапеции взаимно перпендикулярны!
А, если в трапеции со средней линией m1 и диагоналями d1 и d2 выполняется равенство
, то ее площадь можно вычислить по формуле S = 0,5∙d1∙d2.
А, если в трапеции со средней линией m1 и диагоналями d1 и d2 выполняется равенство
, то ее площадь можно вычислить по формуле S = 0,5∙d1∙d2.
Слайд 11Также доказана и справедливость утверждения:
Если 4m22=d12+d22, то S=
(где m2 – вторая средняя линия, а d1 и d2 – диагонали трапеции).
То есть, если выполняется хотя бы одно из вышеупомянутых равенств, то диагонали трапеции взаимно перпендикулярны.
То есть, если выполняется хотя бы одно из вышеупомянутых равенств, то диагонали трапеции взаимно перпендикулярны.
Слайд 12Он был использован при получении другой формулы площади трапеции:
Еще один
способ вывода основной формулы площади трапеции, связан с симметрией параллелограмма
Слайд 20Выводы
В данной исследовательской работе разными способами были получены восемь формул площади
трапеции и следствия из них, показаны их взаимосвязи.
На мой взгляд, цель работы достигнута. В дальнейшем я хочу изучить различные особенности площадей произвольных четырехугольников и их частей.
На мой взгляд, цель работы достигнута. В дальнейшем я хочу изучить различные особенности площадей произвольных четырехугольников и их частей.
