- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Площадь многоугольника презентация
Содержание
- 1. Площадь многоугольника
- 2. Оборудование Компьютер Мультипроектор Мел, доска
- 3. Цели урока Сформировать понятие площади многоугольника, рассмотреть
- 4. Содержание 1.Оргмомент 2.Мозговой штурм 3. Для
- 5. Мозговой штурм Через точку во внутренней области
- 6. Все мы понимаем смысл слов: площадь
- 7. Площадь зеркала водохранилища нужно знать его
- 8. Можно сказать, что площадь многоугольника
- 9. 1см При выбранной единице измерения площадей
- 10. Описанный процесс измерения площадей неудобен, поэтому на
- 11. Площадь прямоугольника Теорема: Площадь прямоугольника равна
- 12. Площадь параллелограмма А В С D
- 13. 2 1 А В С D
- 14. Площадь треугольника Одну из сторон
- 15. Закрепление № 446 Решение:
- 16. Ответы и решения I вариант 1.а) Т.
- 17. Итоги урока 1. Что мы понимаем под
- 18. Домашнее задание п. 48 – 52, № 447, 449(б)
Слайд 3Цели урока
Сформировать понятие площади многоугольника, рассмотреть основные свойства площадей, вывести формулу
Развитие логического мышления
Привитие интереса к предмету геометрии
Слайд 4Содержание
1.Оргмомент
2.Мозговой штурм
3. Для чего нужно уметь измерять и вычислять площади фигур
4.
5. Площадь прямоугольника
6. Закрепление
7. Самостоятельная работа
8. Проверка самостоятельной работы
9. Итоги урока
10. Домашнее задание
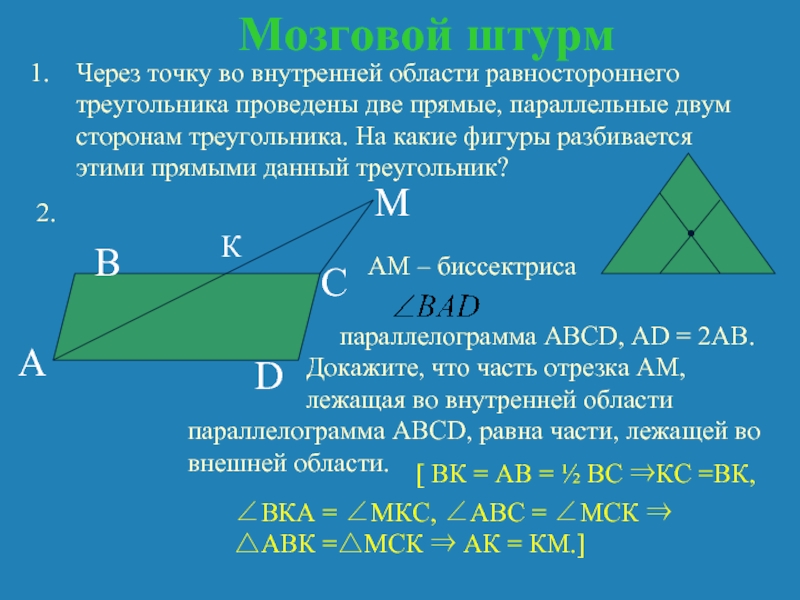
Слайд 5Мозговой штурм
Через точку во внутренней области равностороннего треугольника проведены две прямые,
2.
AM – биссектриса
параллелограмма ABCD, AD = 2AB.
A
B
C
D
M
Докажите, что часть отрезка АМ, лежащая во внутренней области
параллелограмма ABCD, равна части, лежащей во внешней области.
[ ВК = АВ = ½ ВС ⇒КС =ВК,
К
∠ВКА = ∠МКС, ∠АВС = ∠МСК ⇒ △АВК =△МСК ⇒ АК = КМ.]
•
Слайд 6 Все мы понимаем смысл слов: площадь комнаты равна 25 м²
[ прямоугольник: S = ab; круг: S= ]
Площадь поверхности стен в помещении нужно знать, например, для того, чтобы рассчитать необходимое для их покрытия количество обоев, краски или кафеля.
Важно ли в жизни уметь измерять и вычислять площади фигур? Как вы думаете, для чего, например?
Слайд 7
Площадь зеркала водохранилища нужно знать его проектировщикам, в частности, чтобы определить,
Площадь поверхности дороги нужно знать, чтобы рассчитать необходимое для её покрытия количества асфальта.
Слайд 8
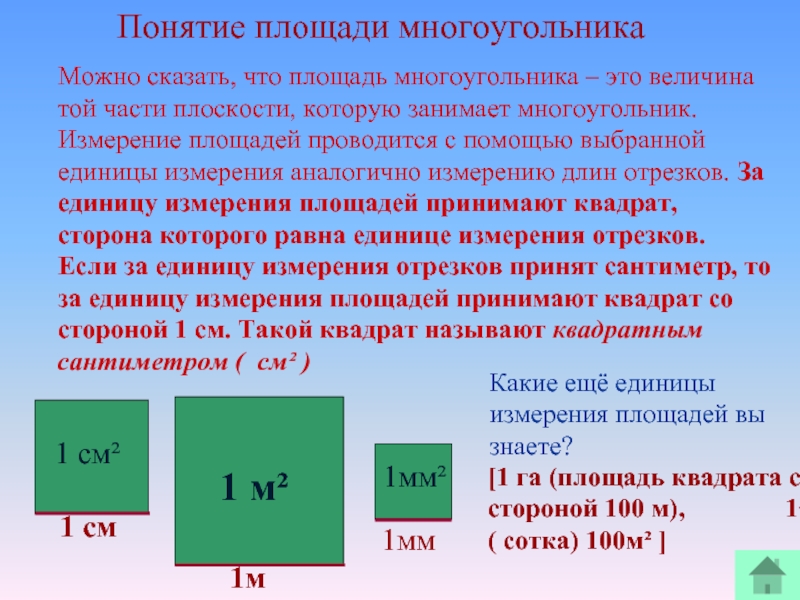
Можно сказать, что площадь многоугольника – это величина той части плоскости,
1 см
1 см²
1м
1мм
1мм²
Какие ещё единицы измерения площадей вы знаете?
[1 га (площадь квадрата со стороной 100 м), 1а ( сотка) 100м² ]
Понятие площади многоугольника
1 м²
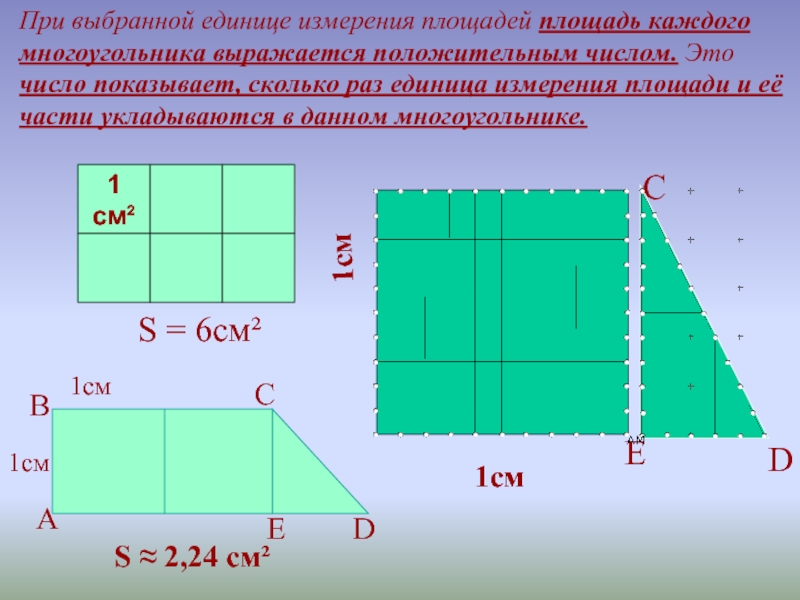
Слайд 91см
При выбранной единице измерения площадей площадь каждого многоугольника выражается положительным числом.
S = 6см²
1 см²
1см
S ≈ 2,24 см²
Слайд 10Описанный процесс измерения площадей неудобен, поэтому на практике измеряют лишь некоторые
1. Равные многоугольники имеют равные площади.
2. Если многоугольник составлен из нескольких многоугольников,то его площадь равна сумме площадей этих многоугольников.
3. Площадь квадрата равна квадрату его стороны
S = S₁ + S₂+ S₃
a
a
S = a²
S₁
S₂
S₃
F₁
F₂
Слайд 11Площадь прямоугольника
Теорема: Площадь прямоугольника равна
b
a
произведению его смежных сторон.
S
S
b
a
b
b
С
a²
b²
a
a
Дано: прямоугольник, a, b – стороны, S – площадь.
Доказать: S = ab
Доказательство:
1) Достроим прямоугольник до квадрата со стороной а + b.
По свойству (3.) его площадь равна ( a + b )² .
S = ab
S
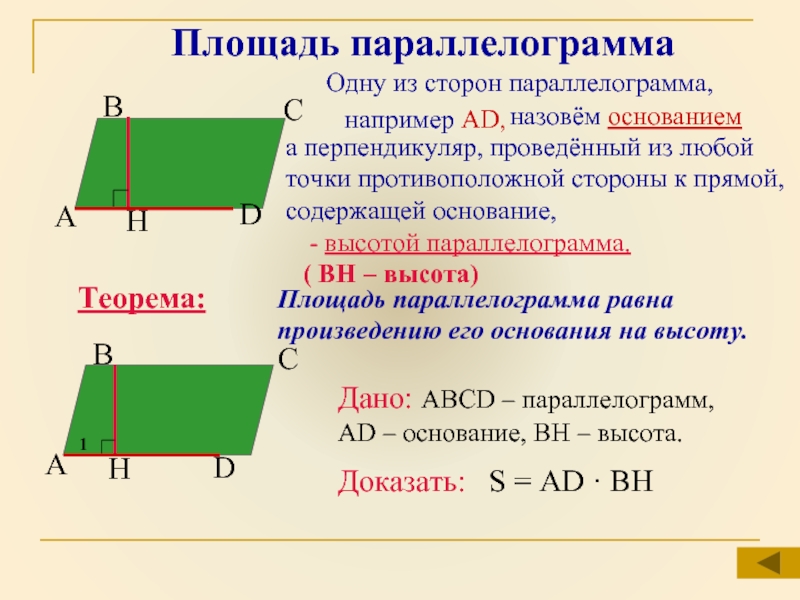
Слайд 12Площадь параллелограмма
А
В
С
D
H
Одну из сторон параллелограмма,
- высотой параллелограмма.
Теорема:
Площадь параллелограмма равна произведению его основания на высоту.
А
В
С
D
H
1
Дано: ABCD – параллелограмм, AD – основание, ВН – высота.
Доказать: S = AD · BH
например AD,
назовём основанием
а перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание,
Слайд 13
2
1
А
В
С
D
H
К
Доказательство:
Пусть площадь параллелограмма равна S.
Параллелограмм ABCD состоит из △ABH
а прямоугольник HBCK – из трапеции HBCD и △DCK. Так как △ABH = △DCK ( по гипотенузе (АВ = DC) и острому углу ( ∠1 = ∠2 как соответственные при AB∥CD ) ).
Значит, , а , но ВС = AD. ⇒
или S = ah, где а – основание, h – высота.
S = ah
Слайд 14
Площадь треугольника
Одну из сторон треугольника (АВ) назовём основанием,
тогда СН – высота
Теорема:
Площадь треугольника равна половине произведения основания на высоту.
Доказать:
Доказательство:
Достроим до параллелограмма.
D
Следствия:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Если высоты двух треугольников равны, то их площади относятся, как основания.
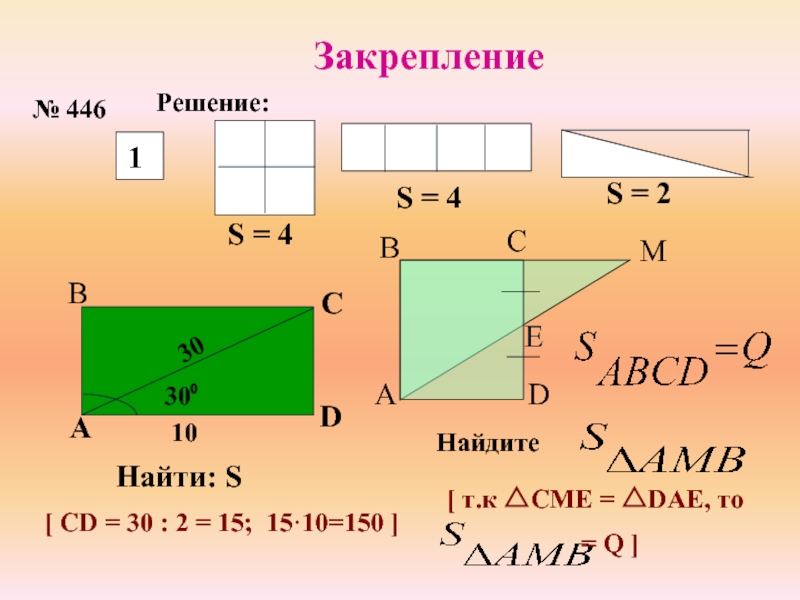
Слайд 15Закрепление
№ 446
Решение:
1
S = 4
S = 4
S = 2
30
30⁰
10
A
B
C
D
Найти: S
[ CD
А
В
C
D
M
Найдите
[ т.к △СМЕ = △DAE, то
= Q ]
E
Слайд 16Ответы и решения
I вариант
1.а) Т. к. АD = 2 АВ, то
АВ = 8 см, AD = 16 см
S = 8·16 S = 128 см²
б) △АВМ = △NCM, ⇒
II вариант
а) АВ = х, ВС = х + 5, (х + х + 5)·2 = 46, 2х + 5 = 23, х = 9
АВ = 9 см, ВС = 14 см
S = 9 · 14, S = 126 см²
б)△FCE =△ADE,⇒
Слайд 17Итоги урока
1. Что мы понимаем под площадью многоугольника?.
2. Перечислить свойства площадей
3.
4. Чему равна площадь параллелограмма?
5. Чему равна площадь треугольника?