Первообразная Интеграл презентация

Содержание

1. Первообразная Интеграл
2. Содержание Понятие первообразной Неопределенный
3. Понятие первообразной Функцию F(x) называют первообразной для
4. Примеры f(x) = 2x; F(x) =
5. Неопределенный интеграл Неопределенным интегралом от непрерывной на
6. Примеры
7. Таблица первообразных f(x) F(x) F(x)
8. Три правила нахождения первообразных 1º Если F(x)
9. Физический смысл первообразной
10. Определенный интеграл – формула Ньютона-Лейбница. Геометрический смысл
11. Вычисление определенного интеграла
12. Площадь криволинейной трапеции a
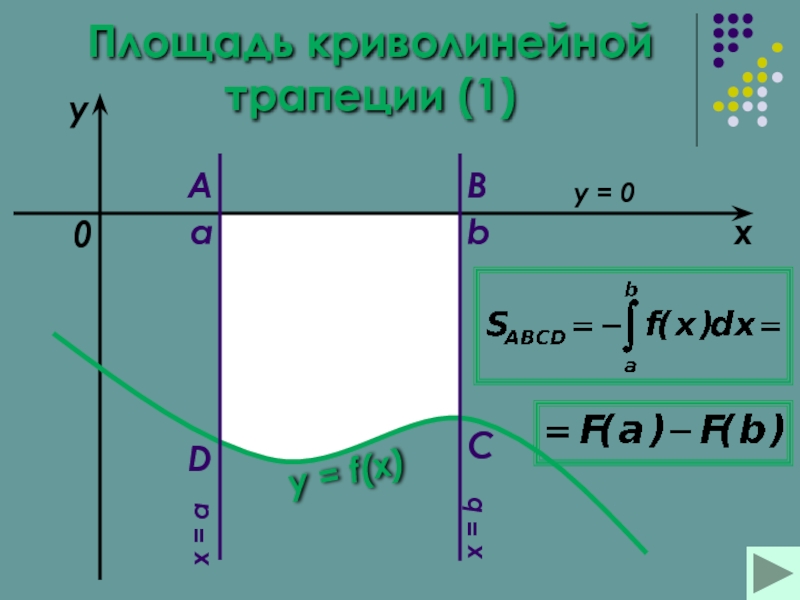
13. Площадь криволинейной трапеции (1)
14. a b x
15. a b x y y
16. Пример 1: вычислить площадь
17. a b x y y
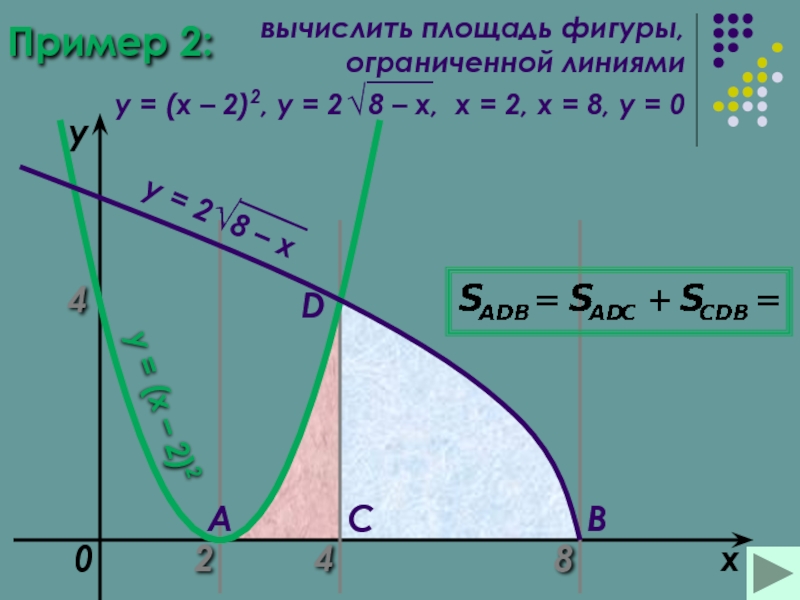
18. Пример 2: 2 8 x
19. Пример 2:

Содержание Понятие первообразной Неопределенный интеграл Таблица первообразных Три правила нахождения первообразных Определенный интеграл Вычисление определенного интеграла Площадь криволинейной трапеции Площадь криволинейной трапеции

Главная
Разное
Первообразная Интеграл

Слайд 1Первообразная Интеграл
МОУ СОШ № 5 – «Школа здоровья и развития»

г. Радужный

Автор: Елена Юрьевна Семёнова

Слайд 2Содержание
Понятие первообразной
Неопределенный интеграл
Таблица первообразных
Три правила нахождения

первообразных
Определенный интеграл
Вычисление определенного интеграла
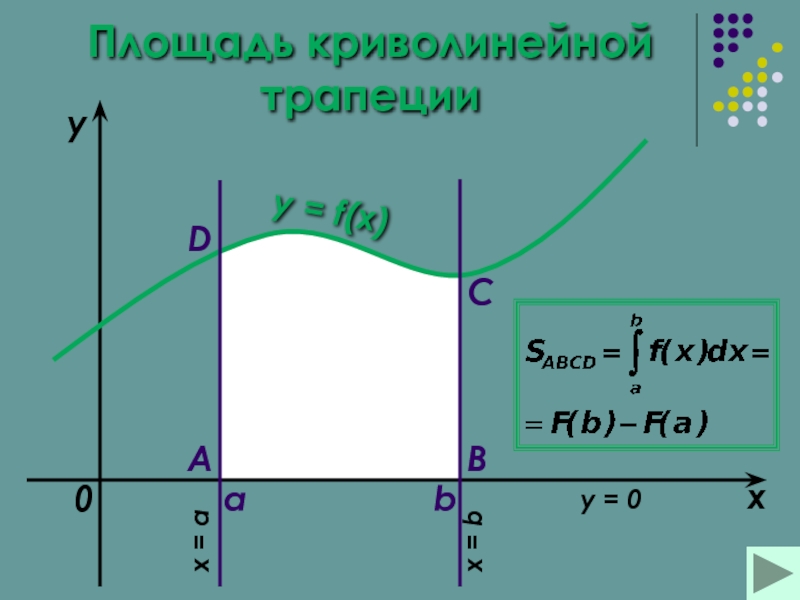
Площадь криволинейной трапеции
Площадь криволинейной трапеции Площадь криволинейной трапеции (1)
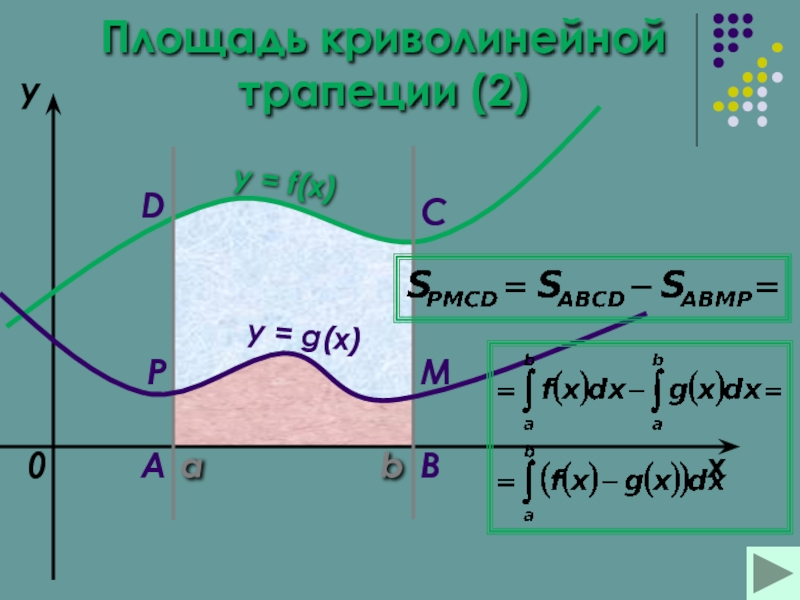
Площадь криволинейной трапеции Площадь криволинейной трапеции (2)
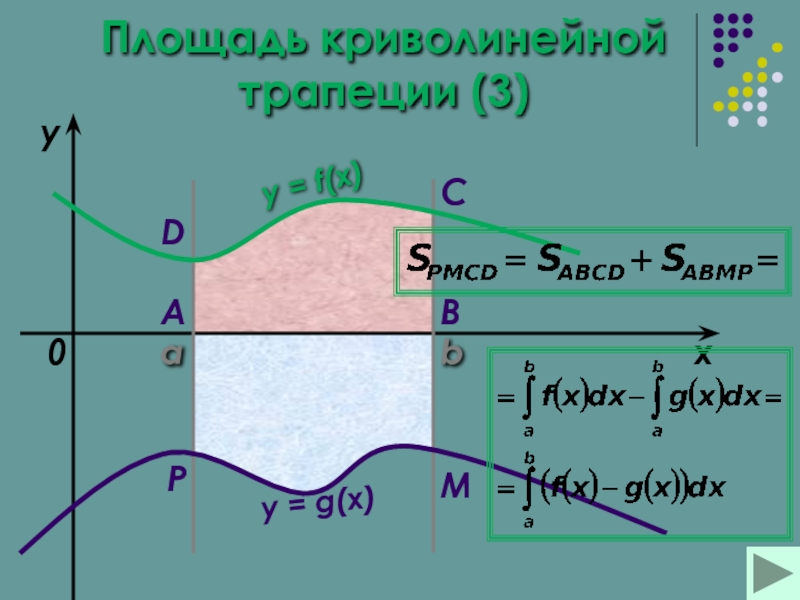
Площадь криволинейной трапеции Площадь криволинейной трапеции (3)
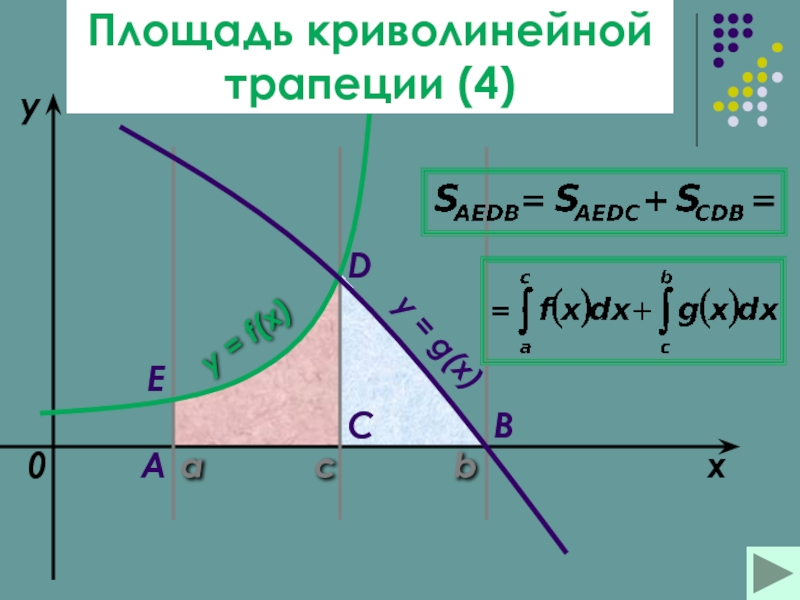
Площадь криволинейной трапецииПлощадь криволинейной трапеции (Площадь криволинейной трапеции (4Площадь криволинейной трапеции (4)
Пример (1)
Пример (2)

Слайд 3Понятие первообразной
Функцию F(x) называют первообразной для функции f(x) на интервале (a;

b), если на нем производная функции F(x) равна f(x):

Операцию, обратную дифференцированию называют интегрированием.

Слайд 4Примеры
f(x) = 2x; F(x) = x2
F′(x)=

(x2)′ = 2x = f(x)

f(x) = – sin x; F(x) = сos x
F′(x)= (cos x)′ = – sin x = f(x)

f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F′(x)= (2x3 + 4x)′ = 6x2 + 4 = f(x)

f(x) = 1/cos2 x; F(x) = tg x
F′(x)= (tg x)′ = 1/cos2 x= f(x)

Слайд 5Неопределенный интеграл
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

называют любую ее первообразную функцию.

Где С – произвольная постоянная (const).

Слайд 6Примеры

Слайд 7Таблица первообразных
f(x)
F(x)
F(x)

Слайд 8Три правила нахождения первообразных
1º Если F(x) есть первообразная для f(x), а

G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).

2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf.

Слайд 9Физический смысл первообразной

Слайд 10Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что

определенный интеграл равен площади криволинейной трапеции, образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.

Слайд 11Вычисление определенного интеграла

Слайд 12
Площадь криволинейной трапеции

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y =

Слайд 13
Площадь криволинейной трапеции (1)

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y

= 0

Слайд 14

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (2)

Слайд 15

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P

Площадь криволинейной трапеции (3)

Слайд 16

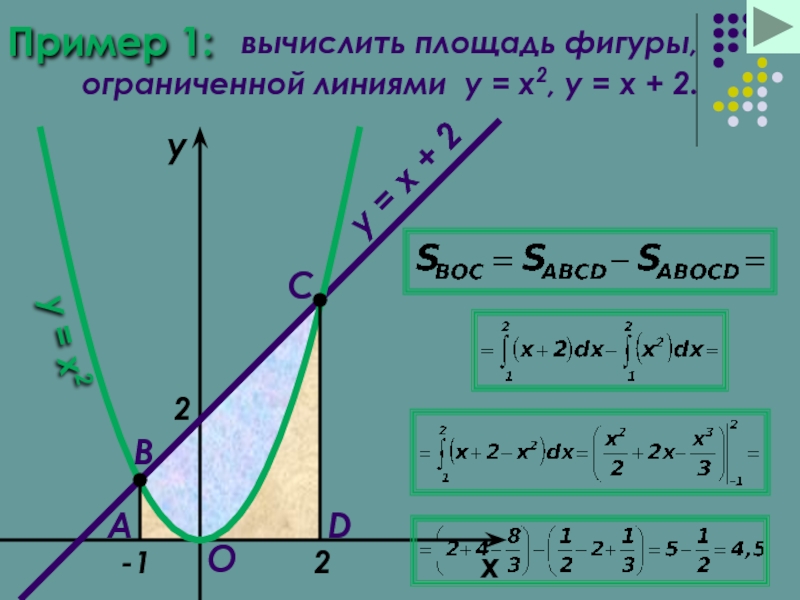
Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y =

x + 2.

y = x2

y = x + 2

-1

Слайд 17

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D

с
Е
Площадь криволинейной трапеции (4)

Слайд 18

Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y

4

Слайд 19Пример 2:

Скачать презентацию

Первообразная Интеграл презентация

Содержание

Слайд 1Первообразная Интеграл
МОУ СОШ № 5 – «Школа здоровья и развития»

Слайд 2Содержание
Понятие первообразной
Неопределенный интеграл
Таблица первообразных
Три правила нахождения

Слайд 3Понятие первообразной
Функцию F(x) называют первообразной для функции f(x) на интервале (a;

Слайд 4Примеры
f(x) = 2x; F(x) = x2
F′(x)=

Слайд 5Неопределенный интеграл
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

Слайд 6Примеры

Слайд 7Таблица первообразных
f(x)
F(x)
F(x)

Слайд 8Три правила нахождения первообразных
1º Если F(x) есть первообразная для f(x), а

Слайд 9Физический смысл первообразной

Слайд 10Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что

Слайд 11Вычисление определенного интеграла

Слайд 12
Площадь криволинейной трапеции

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y =

Слайд 13
Площадь криволинейной трапеции (1)

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y

Слайд 14

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (2)

Слайд 15

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P

Площадь криволинейной трапеции (3)

Слайд 16

Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y =

Слайд 17

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D

с
Е
Площадь криволинейной трапеции (4)

Слайд 18

Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y

4

Слайд 19Пример 2:

Обратная связь

Что такое ThePresentation.ru?

Первообразная Интеграл презентация

Содержание

Слайд 1Первообразная Интеграл МОУ СОШ № 5 – «Школа здоровья и развития»

Слайд 2Содержание Понятие первообразной Неопределенный интеграл Таблица первообразных Три правила нахождения

Слайд 3Понятие первообразнойФункцию F(x) называют первообразной для функции f(x) на интервале (a;

Слайд 4Примерыf(x) = 2x; F(x) = x2 F′(x)=

Слайд 5Неопределенный интегралНеопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

Слайд 6Примеры

Слайд 7Таблица первообразныхf(x)F(x)F(x)

Слайд 8Три правила нахождения первообразных1º Если F(x) есть первообразная для f(x), а

Слайд 9Физический смысл первообразной

Слайд 10Определенный интеграл– формула Ньютона-Лейбница.Геометрический смысл определенного интеграла заключается в том, что

Слайд 11Вычисление определенного интеграла

Слайд 12Площадь криволинейной трапеции abxyy = f(x)0ABCDx = ax = by =

Слайд 13Площадь криволинейной трапеции (1) abxyy = f(x)0ABCDx = ax = by

Слайд 14abxyy = f(x)0y = g(x)ABCDMPПлощадь криволинейной трапеции (2)

Слайд 15abxyy = f(x)0y = g(x)ABCDMPПлощадь криволинейной трапеции (3)

Слайд 16Пример 1:вычислить площадь фигуры, ограниченной линиями y = x2, y =

Слайд 17abxyy = f(x)0y = g(x)ABCDсЕПлощадь криволинейной трапеции (4)

Слайд 18Пример 2:28xy = (x – 2)20ABCD4y4

Слайд 19Пример 2:

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Первообразная Интеграл
МОУ СОШ № 5 – «Школа здоровья и развития»

Слайд 2Содержание
Понятие первообразной
Неопределенный интеграл
Таблица первообразных
Три правила нахождения

Слайд 3Понятие первообразной
Функцию F(x) называют первообразной для функции f(x) на интервале (a;

Слайд 4Примеры
f(x) = 2x; F(x) = x2
F′(x)=

Слайд 5Неопределенный интеграл
Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x)

Слайд 7Таблица первообразных
f(x)
F(x)
F(x)

Слайд 8Три правила нахождения первообразных
1º Если F(x) есть первообразная для f(x), а

Слайд 10Определенный интеграл
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в том, что

Слайд 12
Площадь криволинейной трапеции

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y =

Слайд 13
Площадь криволинейной трапеции (1)

a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y

Слайд 14

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P
Площадь криволинейной трапеции (2)

Слайд 15

a
b
x
y
y = f(x)
0

y = g(x)
A
B
C
D
M
P

Площадь криволинейной трапеции (3)

Слайд 16

Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y =

Слайд 17

a
b
x
y
y = f(x)
0
y = g(x)
A
B
C
D

с
Е
Площадь криволинейной трапеции (4)

Слайд 18

Пример 2:
2
8
x
y = (x – 2)2
0
A
B
C
D
4
y

4