Владимировна
г. Караганды
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОСНОВНЫЕ ПОНЯТИЯ ЛОГИКИ И СУЖДЕНИЙ презентация
Содержание
- 1. ОСНОВНЫЕ ПОНЯТИЯ ЛОГИКИ И СУЖДЕНИЙ
- 2. Вся наша речь состоит из высказываний, то
- 3. Логика — это наука о формах
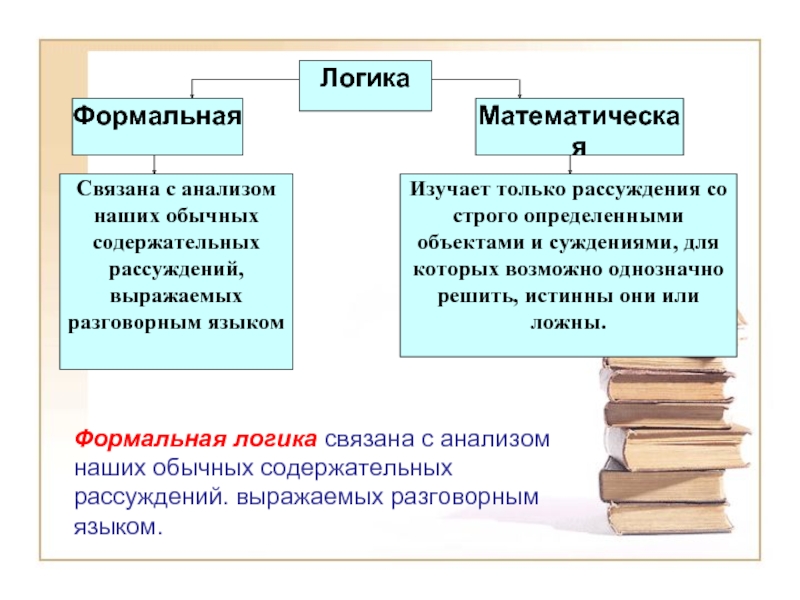
- 4. Логика Формальная Математическая Связана с анализом наших
- 5. Математическая логика является одной из частей формальной
- 6. Алгебра высказываний Алгебра логики изучает идеализированное высказывание,
- 7. Суждения - это некоторые высказывания, которые могут
- 8. Суждения подразделяются на общие и частные.
- 9. Простые высказывания в алгебре логики обозначаются заглавными
- 10. Составные суждения: Этот ученик умный и
- 11. Связка И в составных суждениях
- 12. Связка НЕ применяется для
- 13. 1. Какие из следующих предложений являются высказываниями?
- 14. 2. Определите истинность высказывания. 1)
- 15. Домашнее задание. Прочитать § 3.1. Выполнить задание 3.
- 16. Успехов в изучении информатики!
Слайд 2 Вся наша речь состоит из высказываний, то есть из имеющих смысл
языковых выражений. Высказывания могут быть выражены с помощью естественных языков и формальных.
Например, высказывание на естественном языке имеет вид "пятью пять — двадцать пять", а на формальном, математическом языке оно записывается в виде: "5 * 5 = 25".
Высказывание — законченное по смыслу
предложение, относительно которого
можно утверждать, истинно оно или ложно.
С незапамятных времен существовала
такая наука, как ЛОГИКА
Например, высказывание на естественном языке имеет вид "пятью пять — двадцать пять", а на формальном, математическом языке оно записывается в виде: "5 * 5 = 25".
Высказывание — законченное по смыслу
предложение, относительно которого
можно утверждать, истинно оно или ложно.
С незапамятных времен существовала
такая наука, как ЛОГИКА
Слайд 3
Логика — это наука о формах и законах человеческого мышления и,
в частности, о законах доказательных рассуждений.
Различают несколько вариантов логики как научной дисциплины: формальная логика математическая логика, вероятностная логика, диалектическая логика и т. д.
Различают несколько вариантов логики как научной дисциплины: формальная логика математическая логика, вероятностная логика, диалектическая логика и т. д.
Слайд 4Логика
Формальная
Математическая
Связана с анализом наших обычных содержательных рассуждений, выражаемых разговорным языком
Изучает только
рассуждения со строго определенными объектами и суждениями, для которых возможно однозначно решить, истинны они или ложны.
Формальная логика связана с анализом
наших обычных содержательных
рассуждений. выражаемых разговорным
языком.
Слайд 5 Математическая логика является одной из частей формальной логики и изучает только
v рассуждения со строго определенными объектами и суждениями, для которых возможно однозначно решить, истинны они или ложны.
Вероятностная логика основана на применении больших серий испытаний со случайными параметрами. Точность полученных
результатов зависит от количества
проведенных опытов. Например,
вероятность выпадения "орла" или
"решки" при бросании монеты
равна 1/2, и чем больше произведено
бросаний монеты, тем эта вероятность точнее.
Вероятностная логика основана на применении больших серий испытаний со случайными параметрами. Точность полученных
результатов зависит от количества
проведенных опытов. Например,
вероятность выпадения "орла" или
"решки" при бросании монеты
равна 1/2, и чем больше произведено
бросаний монеты, тем эта вероятность точнее.
Слайд 6Алгебра высказываний
Алгебра логики изучает идеализированное высказывание, относительно которого можно утверждать, истинно
высказывание или ложно. Алгебра логики не вникает в содержание высказываний. Таким
образом, алгебра логики является двухзначной, то есть любое из высказываний может дать
характеристику, передающую одно
из двух значений — "истина" или
"ложь".
образом, алгебра логики является двухзначной, то есть любое из высказываний может дать
характеристику, передающую одно
из двух значений — "истина" или
"ложь".
Слайд 7 Суждения - это некоторые высказывания, которые могут быть истинными или ложными.
Например,
суждения "Снег белый", "2*2=4" истинные, а суждения "Земля плоская", "2*2=5" ложные.
Обычно те факты, которые мы наблюдаем, принимаются за истинные. Ложные
утверждения возникают чаще
всего из-за ошибок в рассуждениях
или предположениях или из-за
стремления выдать желаемое
за действительное.
Обычно те факты, которые мы наблюдаем, принимаются за истинные. Ложные
утверждения возникают чаще
всего из-за ошибок в рассуждениях
или предположениях или из-за
стремления выдать желаемое
за действительное.
Слайд 8
Суждения подразделяются на общие и частные.
Частные суждения выражают конкретные факты,
например "3+3<7", "Сегодня был солнечный день".
Общие суждения характеризуют свойства групп объектов или явлений, например "Если прошел дождь, то на улице мокро", "Любой квадрат является параллелограммом", и т. п.
Общие суждения могут оказаться истинными для какой-то части объектов и ложными
для других объектов.
Например, утверждение
"Собаки не любят кошек" справедливо
для большого числа собак, но
не для всех. Утверждение "х*у>0" истинно
для х=1 и у=1 и в то же время ложно
для х=0 при произвольном у.
Общие суждения характеризуют свойства групп объектов или явлений, например "Если прошел дождь, то на улице мокро", "Любой квадрат является параллелограммом", и т. п.
Общие суждения могут оказаться истинными для какой-то части объектов и ложными
для других объектов.
Например, утверждение
"Собаки не любят кошек" справедливо
для большого числа собак, но
не для всех. Утверждение "х*у>0" истинно
для х=1 и у=1 и в то же время ложно
для х=0 при произвольном у.
Слайд 9 Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Абай
— великий поэт}.
В = {Пушкин А. С. — великий математик}.
Истинному высказыванию ставится в соответствие "1", ложному — "0".
Таким образом: А = 1, В = 0.
В = {Пушкин А. С. — великий математик}.
Истинному высказыванию ставится в соответствие "1", ложному — "0".
Таким образом: А = 1, В = 0.
Слайд 10 Составные суждения:
Этот ученик умный и смышленый.
Это ученик умный.
Этот ученик
смышленый.
Составные высказывания на естественном языке образуются с помощью союзов "И", "ИЛИ", "НЕ", которые в алгебре высказываний заменяются на логические операции.
Составные высказывания на естественном языке образуются с помощью союзов "И", "ИЛИ", "НЕ", которые в алгебре высказываний заменяются на логические операции.
Слайд 11
Связка И в составных суждениях всегда предполагает одновременную истинность составляющих суждений.
Завтра
мы будем работать в саду и парке.
Составное суждений со связкой ИЛИ в математике считается истинным, если истинно хотя бы одно из составляющих суждений, и считается ложным, если ложно все его составляющие.
Завтра мы будем работать в саду или парке.
Составное суждений со связкой ИЛИ в математике считается истинным, если истинно хотя бы одно из составляющих суждений, и считается ложным, если ложно все его составляющие.
Завтра мы будем работать в саду или парке.
Слайд 12
Связка НЕ применяется для формулировок отрицаний. Отрицание истинно, если ложно исходное
утверждение, и, наоборот, отрицание ложно, если верно исходное утверждение.
Слайд 131. Какие из следующих предложений являются высказываниями? Определите их истинность.
1) Сканер
— это устройство ввода информации.
2) Внимание!
3) 5 = 4 + 1
4) Сумма чисел "4" и "1" равна "5".
5) Сумма чисел "4" и "1" не равна "5".
6) 4 + 1 = 5
7) 4 + 1 > 5
8) А — первая буква в алфавите.
9) Сколько в одной тонне килограммов?
10) В одной тонне 1000 килограммов.
11) В одной тонне 100 килограммов.
12) Число 2 — четное.
13) Число 2 — четное?
14) Некоторые ученики моего класса — "отличники".
15) Все ученики моего класса — "отличники".
16) Который час?
17) Сейчас половина одиннадцатого.
2) Внимание!
3) 5 = 4 + 1
4) Сумма чисел "4" и "1" равна "5".
5) Сумма чисел "4" и "1" не равна "5".
6) 4 + 1 = 5
7) 4 + 1 > 5
8) А — первая буква в алфавите.
9) Сколько в одной тонне килограммов?
10) В одной тонне 1000 килограммов.
11) В одной тонне 100 килограммов.
12) Число 2 — четное.
13) Число 2 — четное?
14) Некоторые ученики моего класса — "отличники".
15) Все ученики моего класса — "отличники".
16) Который час?
17) Сейчас половина одиннадцатого.
Слайд 14
2. Определите истинность высказывания.
1) Балхаш — самое глубокое озеро Казахстана.
2) Компьютер
все может.
3) Тигр — хищное животное.
4) Все медведи бурые.
5) Все птицы умеют летать.
6) Принтер — это устройство вывода информации.
7) Луна является спутником Земли.
8) Домбра — казахский народный инструмент.
9) Астана — столица Казахстана.
10) Акын — народный поэт-певец.
3) Тигр — хищное животное.
4) Все медведи бурые.
5) Все птицы умеют летать.
6) Принтер — это устройство вывода информации.
7) Луна является спутником Земли.
8) Домбра — казахский народный инструмент.
9) Астана — столица Казахстана.
10) Акын — народный поэт-певец.