- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимальное квантования презентация
Содержание
- 1. Оптимальное квантования
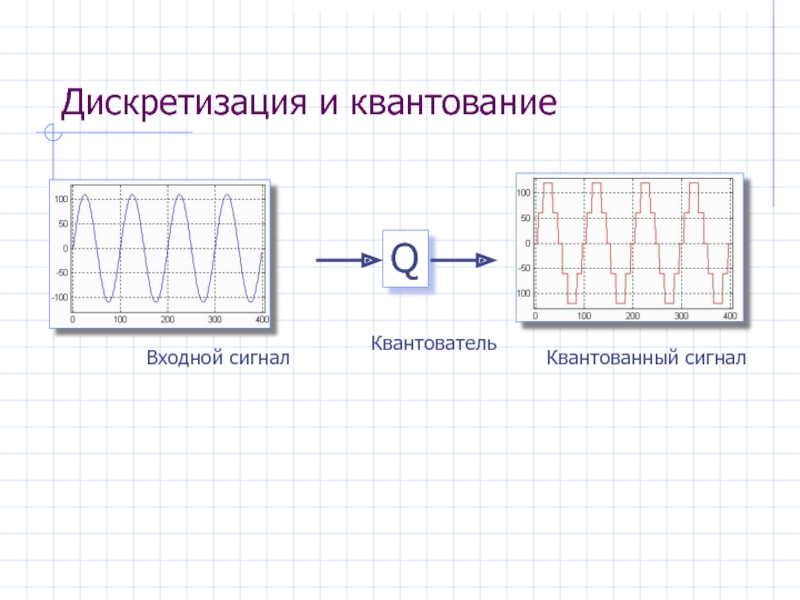
- 2. Дискретизация и квантование Входной сигнал Квантованный сигнал Q Квантователь
- 3. Квантование : область применения АЦП сигналов (audio,video,etc.)
- 4. Квантование & округление Любо действительное число x
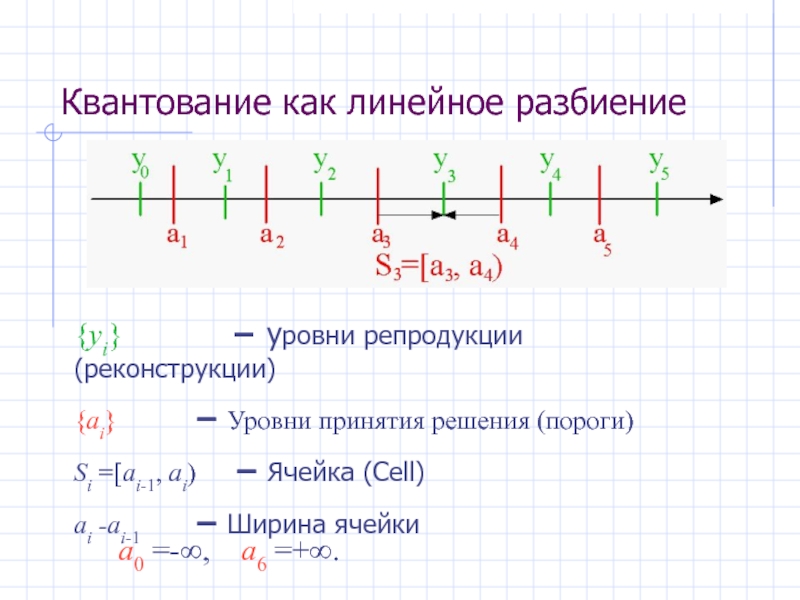
- 5. Квантование как линейное разбиение {yi}
- 6. Неравномерный квантователь: M = 8 уровней Переходная (вход-выход) характеристика неравномерного квантователя R=log2M
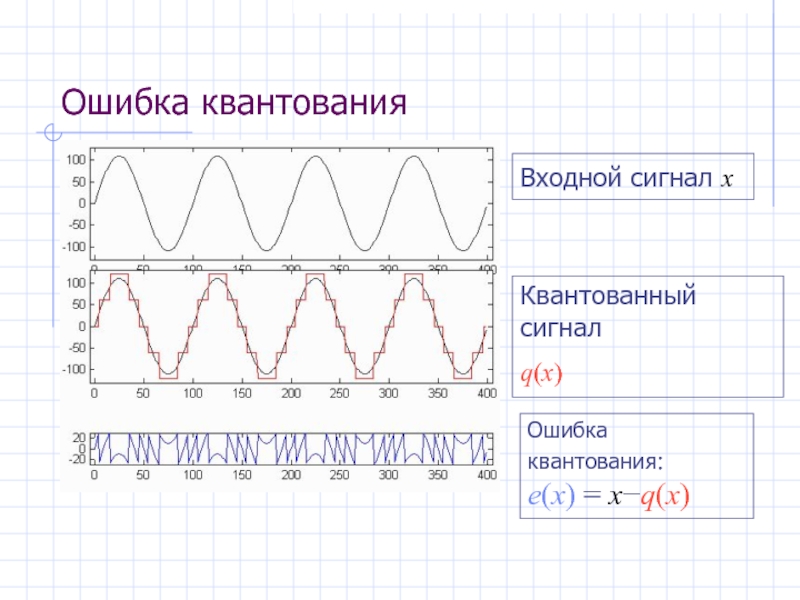
- 7. Ошибка квантования Ошибка квантования: e(x) = x−q(x) Входной сигнал x Квантованный сигнал q(x)
- 8. Измерение искажения: СКО, дисперсия Плотность распределения
- 9. Отношение сигнал –шум
- 10. Источник с равномерным распределением : СКО
- 11. Источник с равномерным распределением : отношение сигнал-шум
- 12. Задача оптимального квантования Задан сигнал x,
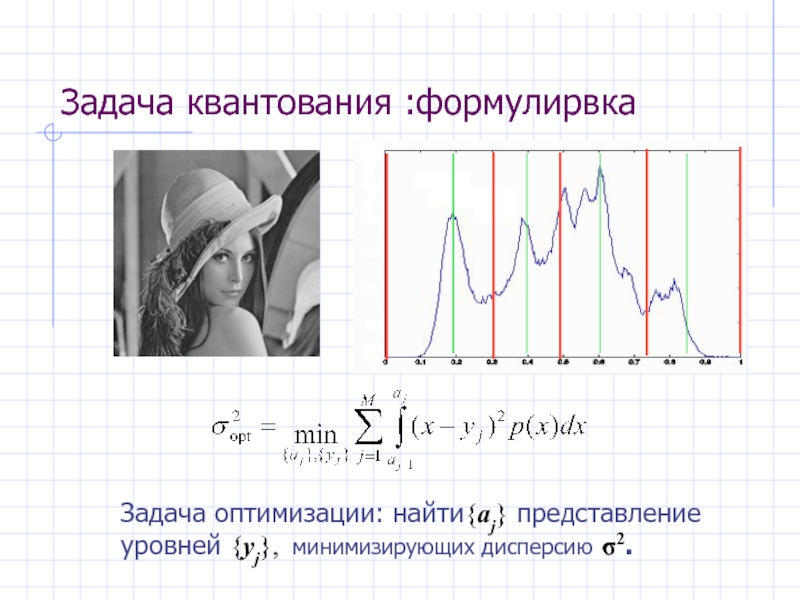
- 13. Задача квантования :формулирвка Задача оптимизации: найти{aj} представление уровней {yj}, минимизирующих дисперсию σ2.
- 14. Скалярный квантователь Max-Lloyd
- 15. Max-Lloyd решение
- 16. Max-Lloyd решение
- 17. Max-Lloyd: условие оптимального квантования Представление уровней yi
- 18. Как конструировать оптимальный квантователь? Если мы
- 19. Max-Lloyd: итеративный алгоритм 0. гипотетическое начальное множество
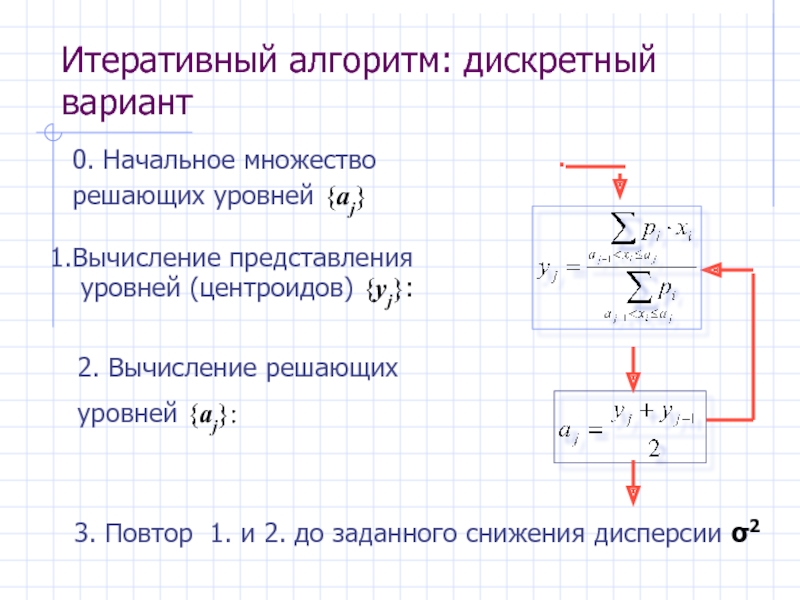
- 20. Итеративный алгоритм: дискретный вариант 0. Начальное множество
- 21. Как построить оптимальный скалярный квантователь? Итеративный
- 22. Lloyd Matlab t = [0:.1:2*pi]; sig =
- 23. Высокоскоростное квантования
- 24. Высокоскоростное квантования Данные X: -∞ <
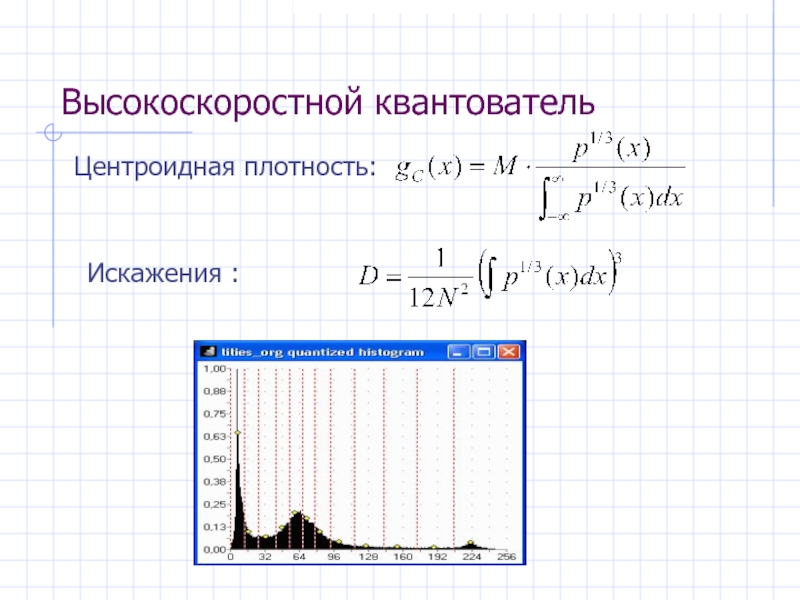
- 25. Центроидная плотность (ЦП) ЦП: gC=1/Δj, один
- 26. Оптимальное высокоскоростное квантование Найти такую
- 27. Метод множителей Лагранжа Преобразуем задачу
- 28. Поиск минимума D* Центроидная плотность: Используем ограничение Для вычисления коэффициента λ.
- 29. Высокоскоростной квантователь Центроидная плотность: Искажения :
- 30. Оптимальный скалярный квантователь
- 31. Формулировка задачи Пусть X={x1, x2,
- 32. Задача разбиения последовательности Ошибка квантования для
- 33. Задача оптимизации Для заданных данных X,
- 34. Функция стоимости DM(0,N] Положим, мы введем
- 35. Подход динамического программирования (ДП) Окончательно: Перепишем функцию стоимости в виде:
- 36. Рекуррентное уравнение Инициализация : Рекурсия :
- 37. Оптимальное скалярное квантование Оптимальный скалярный квантователь
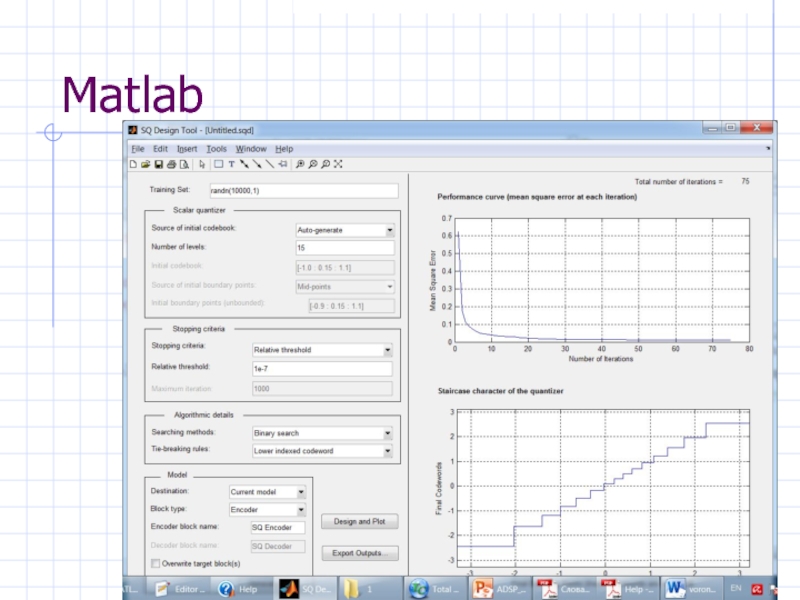
- 38. Matlab
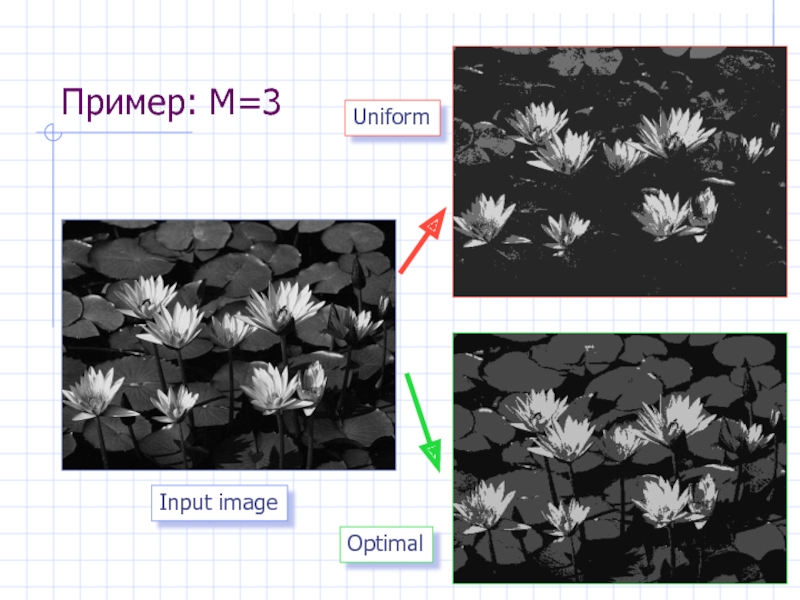
- 39. Пример: M=3 Input image Uniform Optimal
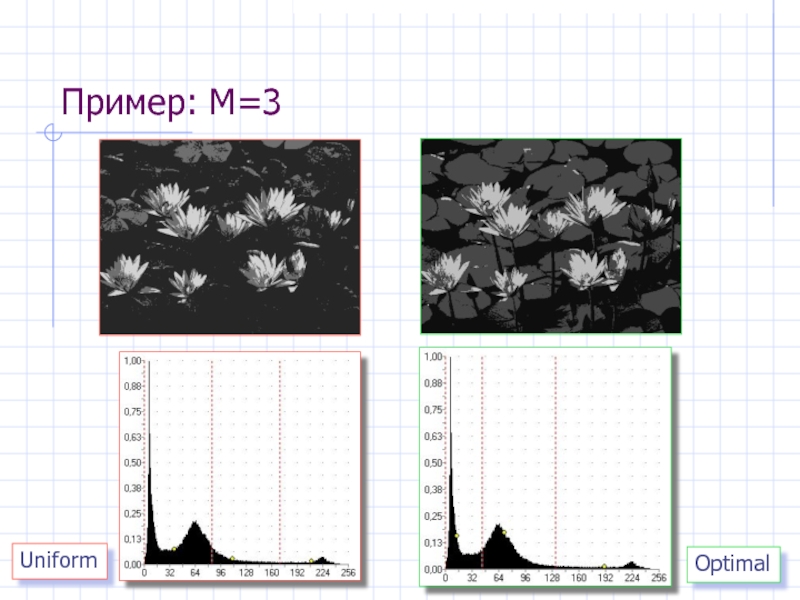
- 40. Пример: M=3 Uniform Optimal
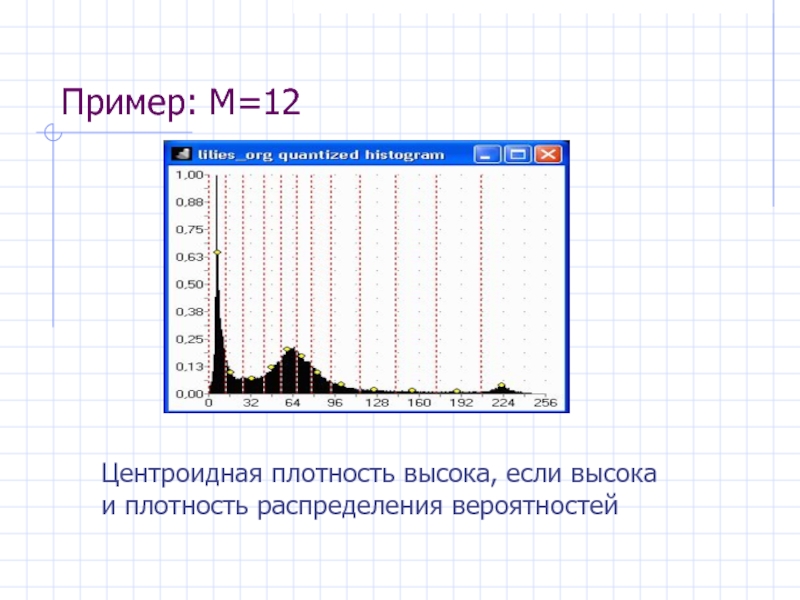
- 41. Пример: M=12 Центроидная плотность высока, если высока и плотность распределения вероятностей
- 42. Высокоскоростное квантования
- 43. Векторное квантование
- 44. VQ: определение ∙ ∙ ∙ ∙ ∙
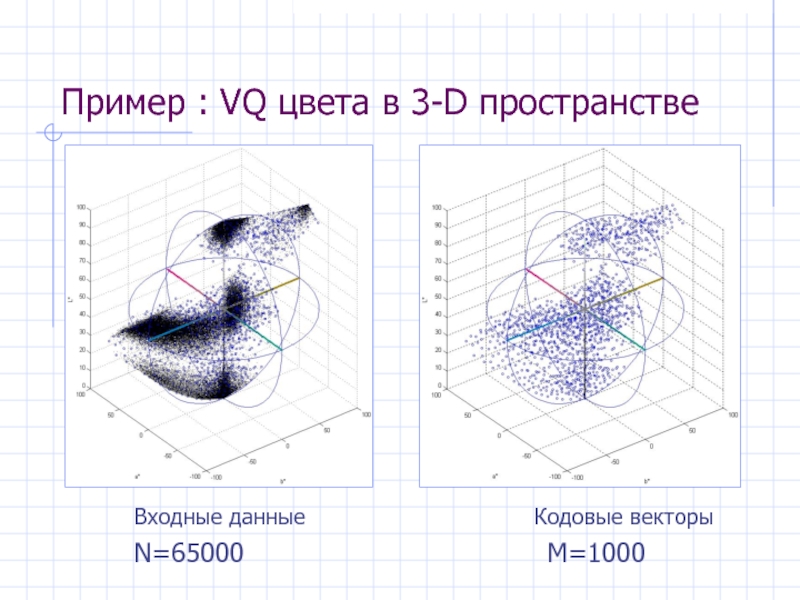
- 45. Пример : VQ цвета в 3-D пространстве Входные данные Кодовые векторы N=65000 M=1000
- 46. VQ voronoi(rand(100,1), rand(100,1)) set(gca, 'visible', 'off')
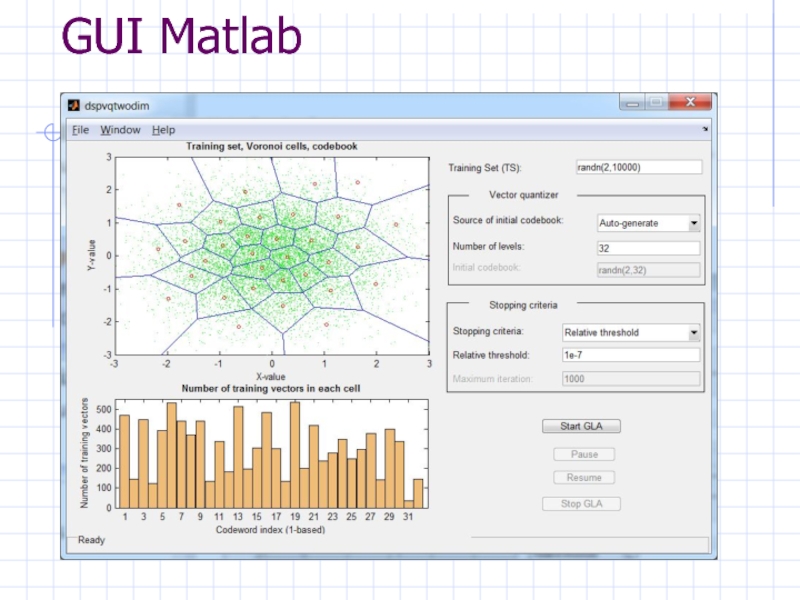
- 47. GUI Matlab
- 48. Вопросы Спасибо за внимание
Слайд 3Квантование : область применения
АЦП сигналов (audio,video,etc.)
Бинаризация и многоуровневая пороговая обработка
цифрового изображения
Квантование
(JPEG, JPEG2000)
Слайд 4Квантование & округление
Любо действительное число x может быть округлено к ближайшему
If k−0.5 ≤ x 5 5.5 6 6.5 7 x=6.4 x=5.6 q(x)=6.0
Слайд 5Квантование как линейное разбиение
{yi} − уровни репродукции
{ai} − Уровни принятия решения (пороги)
Si =[ai-1, ai) − Ячейка (Cell)
ai -ai-1 − Ширина ячейки
a0 =-∞, a6 =+∞.
Слайд 6Неравномерный квантователь:
M = 8 уровней
Переходная (вход-выход) характеристика
неравномерного квантователя
R=log2M
Слайд 8Измерение искажения: СКО, дисперсия
Плотность распределения вероятности (РВ) x определим как
Ошибка квантования: e(x) = x − q (x)
Среднее значение μ ошибки квантования:
Дисперсия σ2 ошибки квантования :
Слайд 10Источник с равномерным распределением : СКО
Данные x -> 0-среднее значение,
Шаг равномерного распределения: Δ=A/M.
Слайд 11Источник с равномерным распределением : отношение сигнал-шум
Данные x -> 0-среднее
Число бит: R=log2M, M – число уровней или M=2R ячеек.
Шаг равномерного квантования : Δ=A/M
”6 dB per bit rule”
Цена 1 бита в квантователе ⇒ 6 dB в отношении сигнал-шум
Слайд 12Задача оптимального квантования
Задан сигнал x, с плотностью распределения вероятности(ПРВ) (или гистограмма)
Требуется: найти квантователь q(x) сигнала x, который минимизирует дисперсию ошибки квантования σ2:
Слайд 13Задача квантования :формулирвка
Задача оптимизации: найти{aj} представление уровней {yj}, минимизирующих дисперсию σ2.
Слайд 17Max-Lloyd: условие оптимального квантования
Представление уровней yi -центроиды:
Решающие уровни ai среднее 2
yj+1
yj
aj
yj-1
aj-1
Слайд 18Как конструировать оптимальный квантователь?
Если мы имеем некоторое множество уровней и
удовлетворяют ли эти уровни критерию минимума
дисперсии ошибки
Но уравнения не говорят нам как найти
оптимальные уровни
?
Слайд 19Max-Lloyd: итеративный алгоритм
0. гипотетическое начальное множество
решающих уровней {aj}
Вычисление представление
(центроидов) {yj}:
2. Вычисление решающих
уровней {aj}:
3. Повтор 1. и 2. до заданного снижения дисперсии σ2
∙
Слайд 20Итеративный алгоритм: дискретный вариант
0. Начальное множество
решающих уровней {aj}
Вычисление представления
уровней (центроидов)
2. Вычисление решающих
уровней {aj}:
3. Повтор 1. и 2. до заданного снижения дисперсии σ2
∙
Слайд 21Как построить оптимальный скалярный квантователь?
Итеративный алгоритм Ллойда не может гарантировать
Слайд 22Lloyd Matlab
t = [0:.1:2*pi];
sig = sin(t);
partition = [-1:.2:1];
codebook = [-1.2:.2:1];
% Now
[partition2,codebook2] = lloyds(sig,codebook);
[index,quants,distor] = quantiz(sig,partition,codebook);
[index2,quant2,distor2] = quantiz(sig,partition2,codebook2);
% Compare mean square distortions from initial and optimized
[distor, distor2] % parameters.
ans =
0.014798675568578 0.002223655629773
Слайд 24Высокоскоростное квантования
Данные X: -∞ < x < ∞ ; p(x)
Положим, что p(x) имеет вид плоской функции над ячейкой Cj
Квантование в M ячейках: M >> 1.
Искажение для ячейки Cj с учетом выдвинутых предположений:
Искажение для равномерного квантователя: D=Δ2/12
Слайд 25Центроидная плотность (ЦП)
ЦП: gC=1/Δj, один центроид для одной ячейки.
В
В этом случае искажение в одной ячейки оценивается как
Общее искажение D:
Слайд 26Оптимальное высокоскоростное квантование
Найти такую ЦП gC(x) которая минимизирует
общее искажение
ограничение:
Слайд 27Метод множителей Лагранжа
Преобразуем задачу в задачу оптимизации
без ограничений с
Найдем минимум стоимостной функции Лагранжа:
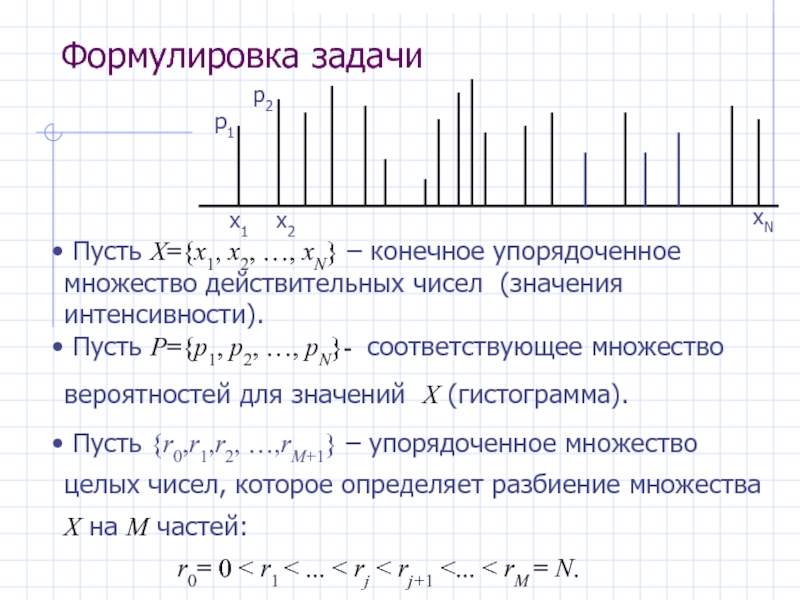
Слайд 31Формулировка задачи
Пусть X={x1, x2, …, xN} – конечное упорядоченное множество
Пусть P={p1, p2, …, pN}- соответствующее множество вероятностей для значений X (гистограмма).
Пусть {r0,r1,r2, …,rM+1} – упорядоченное множество целых чисел, которое определяет разбиение множества X на M частей:
r0= 0 < r1 < ... < rj < rj+1 <... < rM = N.
x1 x2
xN
p1
p2
Слайд 32Задача разбиения последовательности
Ошибка квантования для одной ячейки:
Центроид ячейки
Индексы разбиения: r0= 0 < r1 <... < rj < ... < rM =N.
(r0= 0 для x0= −∞.)
Общая ошибка квантования:
Слайд 33Задача оптимизации
Для заданных данных X, вероятностей P и числа ячеек
найти такое разбиение {ro,r1, r2, …, rM} которое приводит
к минимуму общую ошибку квантования :
где
и
Слайд 34Функция стоимости DM(0,N]
Положим, мы введем в рассмотрение функцию стоимости Dm(0,n]
Xn={x1, x2, …, xn} из m ячеек:
Тогда DM(0,N] дает решение задачи .
Слайд 35Подход динамического программирования (ДП)
Окончательно:
Перепишем функцию стоимости в виде:
Слайд 37Оптимальное скалярное квантование
Оптимальный скалярный квантователь определяет наикратчайший путь во взвешенном
ДП алгоритм [1963]: временная сложностьs O(MN2)
Wu [1991] уменьшил временную сложность оптимального ДП алгоритма до O(MN)
X,Y,Z [2003] ”Fast algorithm for multilevel thresholding”:
O(NM)→ O(NM-1)
Слайд 41Пример: M=12
Центроидная плотность высока, если высока
и плотность распределения вероятностей
Слайд 44VQ: определение
∙
∙
∙
∙
∙
∙
∙
∙
∙
∙
X={x1,x2,…,xN } есть множество входных векторов в d-D
c={c1,c2,…,cM} множество кодовых векторов в пространстве
P разбиение пространства на M кодовых ячеек (кластеров)
C={C1,C2,…,CM}
∙
∙
VQ имеет NP-сложность!










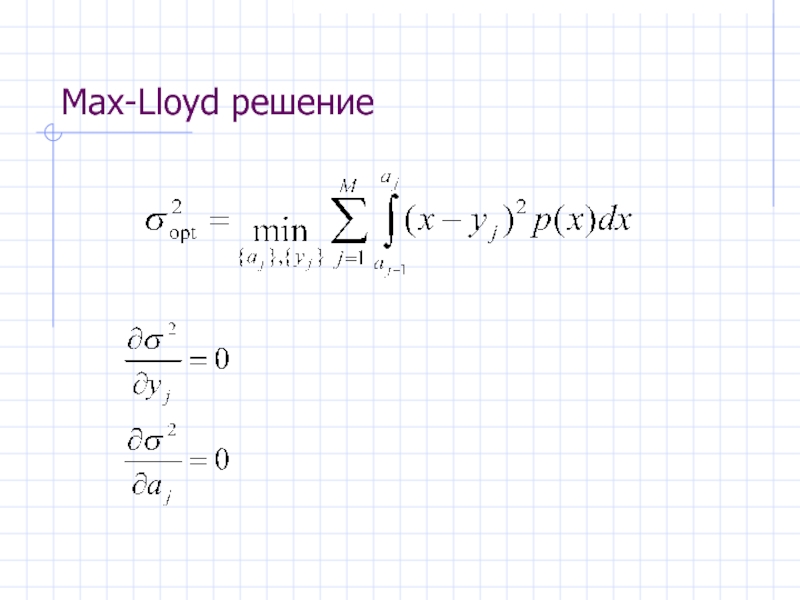





![Lloyd Matlabt = [0:.1:2*pi];sig = sin(t);partition = [-1:.2:1];codebook = [-1.2:.2:1];% Now optimize, using codebook as](/img/tmb/4/351180/7abb2d5bdc622eed309b9ec7d44a956e-800x.jpg)









![Функция стоимости DM(0,N] Положим, мы введем в рассмотрение функцию стоимости Dm(0,n] которая минимизирует ошибку квантования](/img/tmb/4/351180/73367b11ea91c4276e1b0c8c44ba8d70-800x.jpg)