- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определение производной. Геометрический смысл производной. Приложение производной к решению задач презентация
Содержание
- 1. Определение производной. Геометрический смысл производной. Приложение производной к решению задач
- 3. Отгадайте ключевое слово урока 1) С ее
- 4. Исторические сведения Производная – одно из фундаментальных
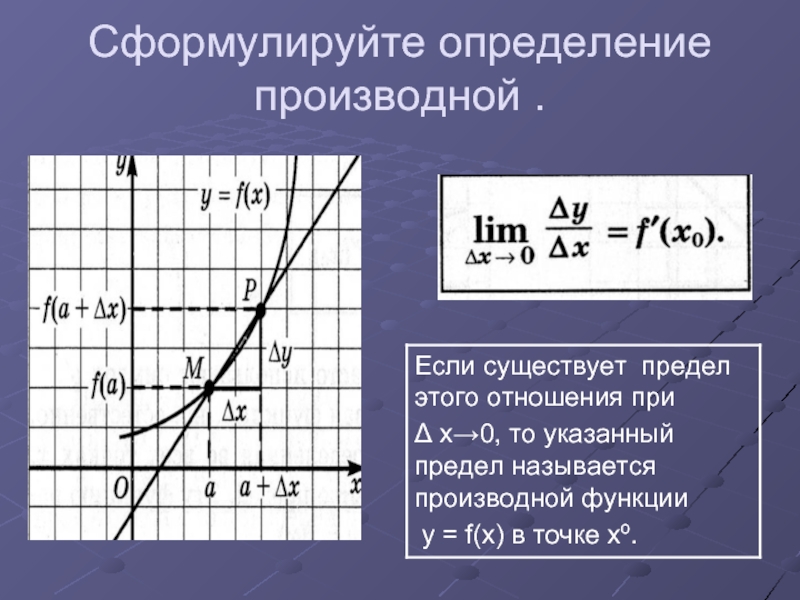
- 5. Сформулируйте определение производной .
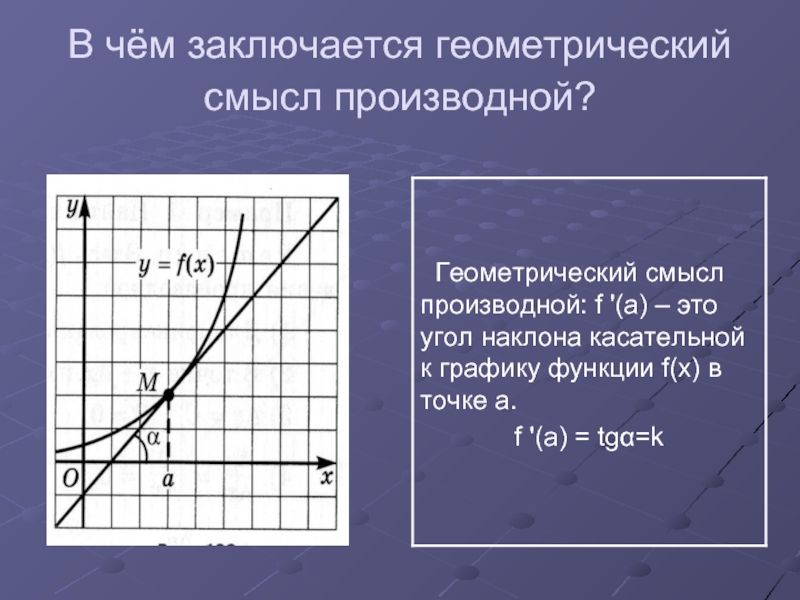
- 6. В чём заключается геометрический смысл производной?
- 7. Правила дифференцирования (u+v)' =
- 8. Уравнение касательной
- 9. Алгоритм нахождения наименьшего и наибольшего значения функцииy=f(x)
- 10. При исследовании свойств функции следует найти
- 11. Найти производную
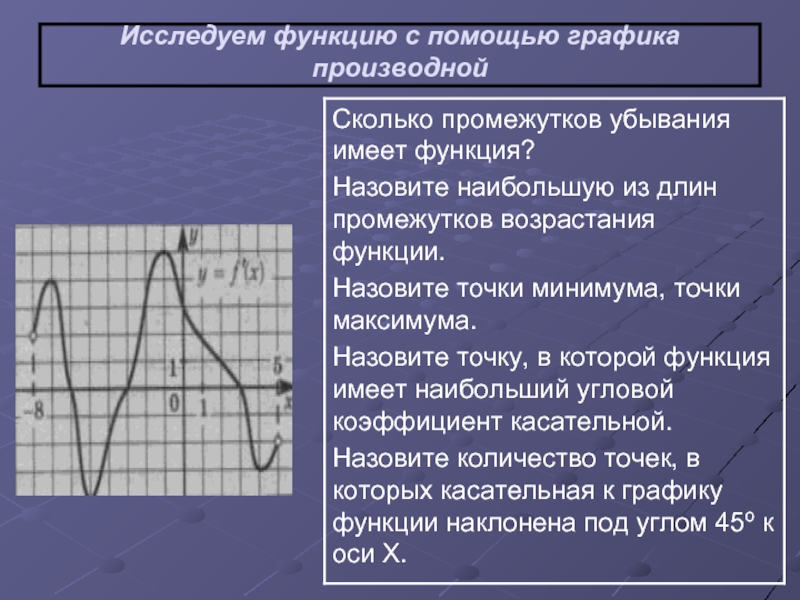
- 12. Исследуем функцию с помощью графика производной
- 13. «Что бы это значило?»
- 14. «Что бы это значило?»
- 15. Приложения производной Применении производной в геометрии(касательная к
- 16. Построение касательной и нормали к графику функции
- 17. Групповая работа
- 18. Задание 1 группы Задача №1.
- 19. Задание 2 группы Составить уравнение общих
- 20. «Лишь дифференциальное исчисление дает
- 21. Задание для всех групп Что вы можете
- 22. Домашнее задание составить тест по теме «Применение
Слайд 1«Определение производной. Геометрический смысл производной.
Приложение производной к решению задач»
Выполнили:
Кенжимбетова Г.У.
2011
Слайд 3Отгадайте ключевое слово урока
1) С ее появлением математика перешагнула из алгебры
2) Ньютон назвал ее «флюксией» и обозначал точкой;
3) Бывает первой, второй,… ;
4) Обозначается штрихом.
Слайд 4Исторические сведения
Производная – одно из фундаментальных понятий
математики. Оно возникло в
от друга И.Ньютон и Г.Лейбниц разработали основные
элементы дифференциального исчисления.
«Метод флюкций». Так Ньютон назвал свою работу,
посвященную основным понятиям математического
анализа. Функцию Ньютон назвал флюентой,
а производную – флюкцией. Обозначения Ньютона
для производных - х* (с точкой) и у* - сохранились
в физике до сих пор.
Исчисление, созданное Ньютоном и Лейбницем, получило название дифференциального исчисления. С его помощью был решен целый ряд задач теоретической механики, физики и астрономии.
Слайд 9Алгоритм нахождения наименьшего и наибольшего значения функцииy=f(x) на отрезке [a; b]
1.
2. Найдите стационарные и критические точки функции, лежащие внутри отрезка [a;b ].
3. Вычислить значения функции y=f(x) в точках, отобранных на втором шаге, и в точках a и b;выбрать среди этих значений наименьшее и наибольшее .
Слайд 10 При исследовании свойств функции следует найти
Область определения функции
Производную
Критические точки функции (производная равна 0 или не существует)
Промежутки возрастания и убывания
Точки экстремума и сами экстремумы.
Слайд 15Приложения производной
Применении производной в геометрии(касательная к графику функции).
Применении производной в физике
Применение производной к исследованию функции.
Применение производной к решению задач на нахождение наибольшего и наименьшего значения функции.
Слайд 16Построение касательной и нормали к графику функции у = f(x) в
Упражнение 1.
Написать уравнение касательной и нормали к графику функции у = f(х)
в точке с абсциссой а=1.
Решение:
f(x)=x –x, а=1
f (x)=3x -1
f (a) = 3*1-1 = 2
f(a) = 0
y - 0 = 2(x-1)
y = 2x- 2 – уравнение касательной
y - 0 = -1/2 * (х-1)
y = -1/2x+1/2 – уравнение нормали
Ответ: y = 2x- 2, y = -1/2x+1/2
Слайд 18Задание 1 группы
Задача №1.
Тело массой m кг движется по
Задача №2.
Материальная точка движется по закону х(t)=- t3 +6 t2 +5 t ( х – в метрах, t – в секундах).
Определите скорость точки в момент, когда ее ускорение равно нулю.
Слайд 19Задание 2 группы
Составить уравнение общих касательных к кривым
f(x)=х² +4х +8
Слайд 20
«Лишь дифференциальное исчисление
дает естествознанию возможность
изображать математически не только
состояния, но
Ф.Энгельс
Слайд 21Задание для всех групп
Что вы можете сказать о производной функции, которую
Каким может быть график функции, которая соответствует поговорке «Больше меры конь не скачет»?
Слайд 22Домашнее задание
составить тест по теме «Применение производной». Задания могут быть с
Найти производную
Найти точки максимума или минимума
Найти промежутки возрастания или убывания
Найти наибольшее значение функции и т.д






![Алгоритм нахождения наименьшего и наибольшего значения функцииy=f(x) на отрезке [a; b]1. Найдите производную.2. Найдите стационарные](/img/tmb/1/84795/ce8e49fbbb54d4c6395e8e5eec3a9c46-800x.jpg)