- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обзор современного состояния области алгоритмов и структур данных презентация
Содержание
- 1. Обзор современного состояния области алгоритмов и структур данных
- 2. Идеи
- 3. План Computer Science Web-графы Случайные графы Highway
- 4. Теоретики
- 5. Практики
- 6. Программисты
- 7. Эдгар Дейкстра
- 8. Никлаус Вирт
- 9. Чарльз Хоар
- 10. Дональт Кнут
- 11. Программа +
- 12. Computer Science Закон Вирта Программы становятся медленне
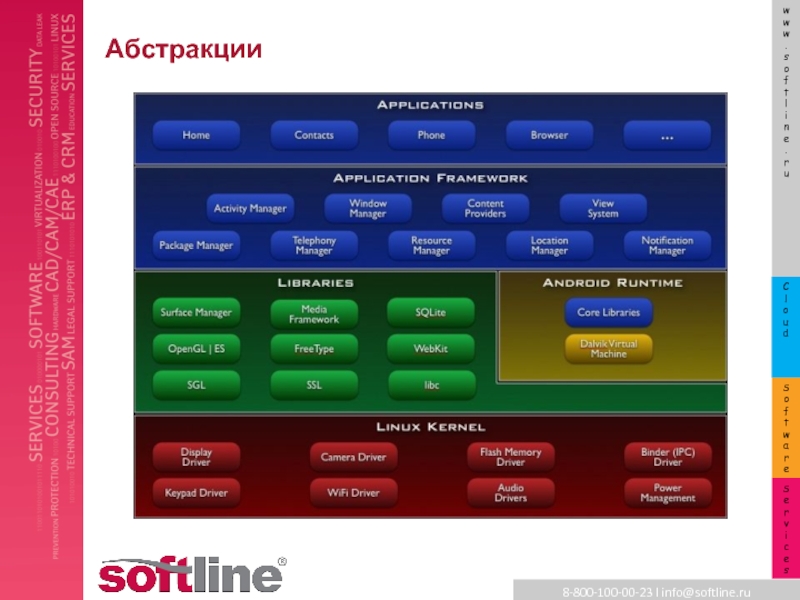
- 13. Абстракции
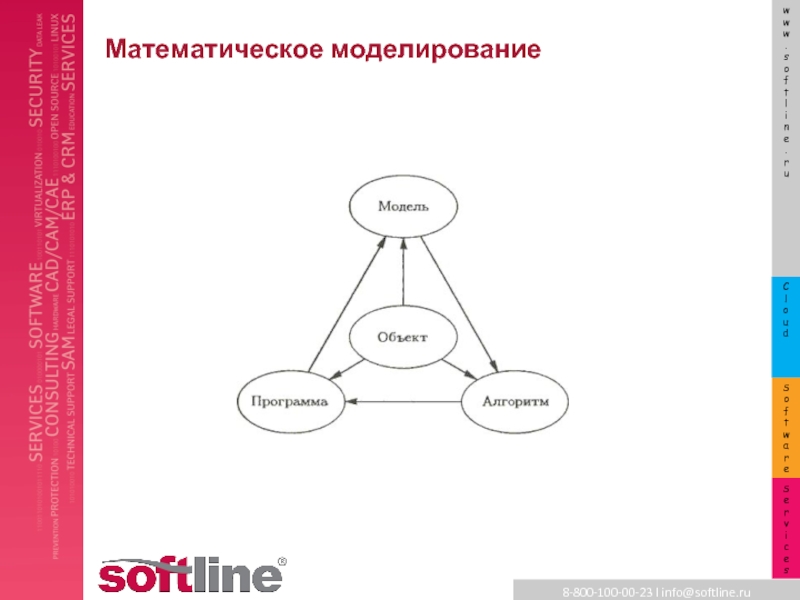
- 14. Математическое моделирование
- 15. Теория графов + Теория вероятностей = PROFIT +
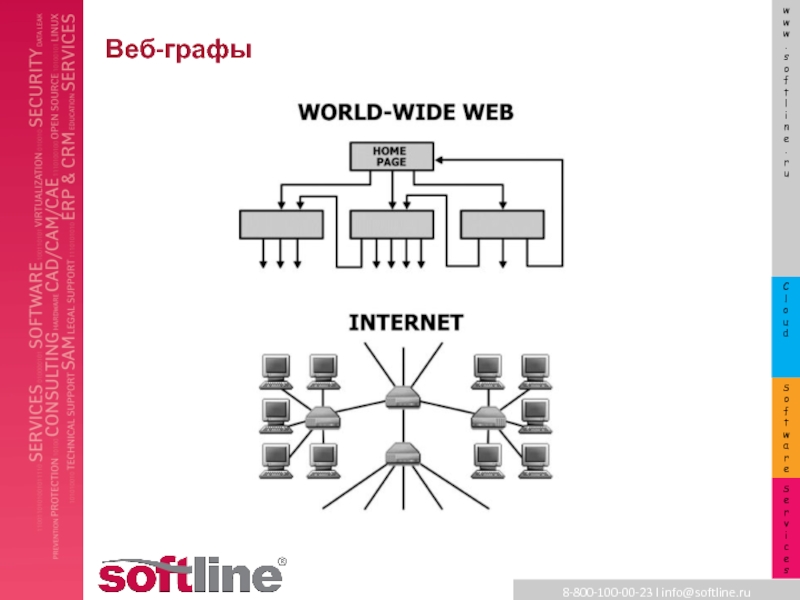
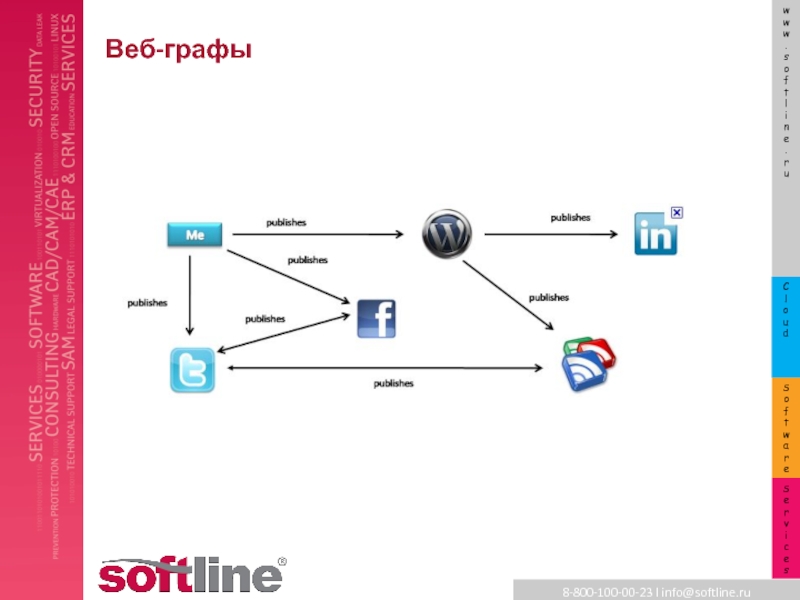
- 16. Веб-графы
- 17. Веб-графы
- 18. Случайные графы Наблюдения Барабаши-Альберт Как устроен
- 19. Случайные графы Наблюдения Барабаши-Альберт
- 20. Случайные графы Модель Эрдёша-Реньи G(n,p) V =
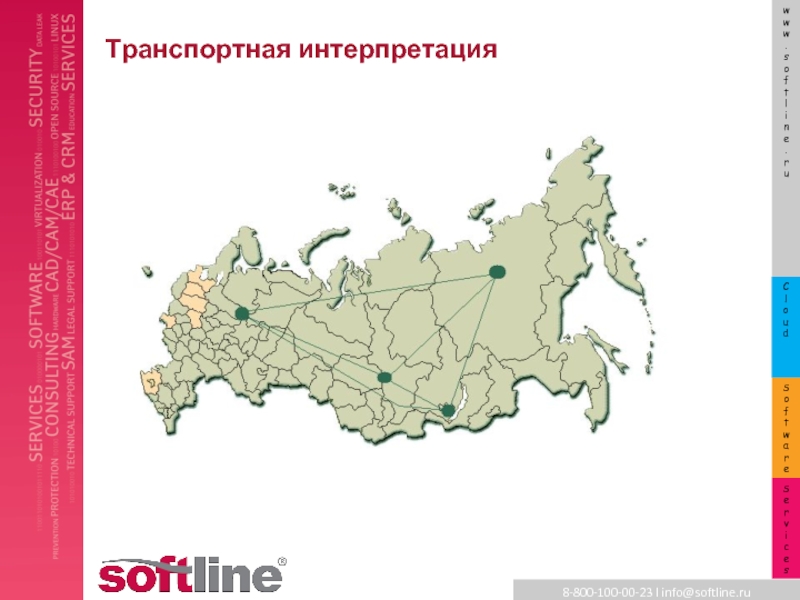
- 21. Транспортная интерпретация
- 22. Highway dimension
- 23. Highway dimension Почему современные алгоритмы на
- 24. P vs NP
- 25. 1 миллион долларов!
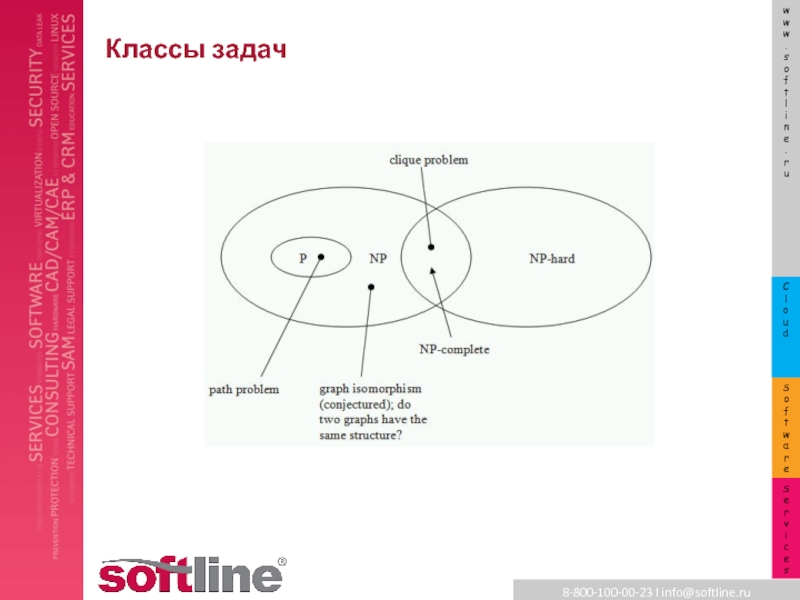
- 26. Классы задач
- 27. P vs NP Задача поиска задаётся алгоритмом
- 28. Андрей Михайлович Райгородский
- 29. Андрей Гольдберг
- 30. Что осталось нерассмотренным Параллельные алгоритмы Распознавание изображений
- 31. Так говорил Дейкстра I think it wise,
Слайд 1Обзор современного состояния области алгоритмов и структур данных
Калачёв Максим Александрович
Разработчик
maxkalachev@yandex.ru
Слайд 3План
Computer Science
Web-графы
Случайные графы
Highway dimenstion
NP vs P
Что осталось нерассмотренным
Послесловие
Слайд 12Computer Science
Закон Вирта
Программы становятся медленне более быстро, чем компьютеры становятся быстрее
P
=
A =
Mρ - множество процедур решения задачи
R2 ⊂ Mρ ² - бинарное отношение на Mρ
(ρi, ρj) ∈ R2 ⇔ после пройедуры ρi выполняется процедура ρj
A =
Mρ - множество процедур решения задачи
R2 ⊂ Mρ ² - бинарное отношение на Mρ
(ρi, ρj) ∈ R2 ⇔ после пройедуры ρi выполняется процедура ρj
Слайд 18Случайные графы
Наблюдения Барабаши-Альберт
Как устроен web-граф?
Barabashi, Albert, 1999, 2000
5 млрд вершин, псевдомультиорграф
Ключевые
свойства веб-графа:
∙ Разрежённость
на k вершин kt рёбер, k ≥ 1
∙ Диаметр графа ∈ {5, 6}
Теория о шести рукопожатиях
∙ Степенное распределение степеней вершин
P(d) ∼ c / d λ
λ ≈ 2.1, c – нормирующий множитель
∙ Разрежённость
на k вершин kt рёбер, k ≥ 1
∙ Диаметр графа ∈ {5, 6}
Теория о шести рукопожатиях
∙ Степенное распределение степеней вершин
P(d) ∼ c / d λ
λ ≈ 2.1, c – нормирующий множитель
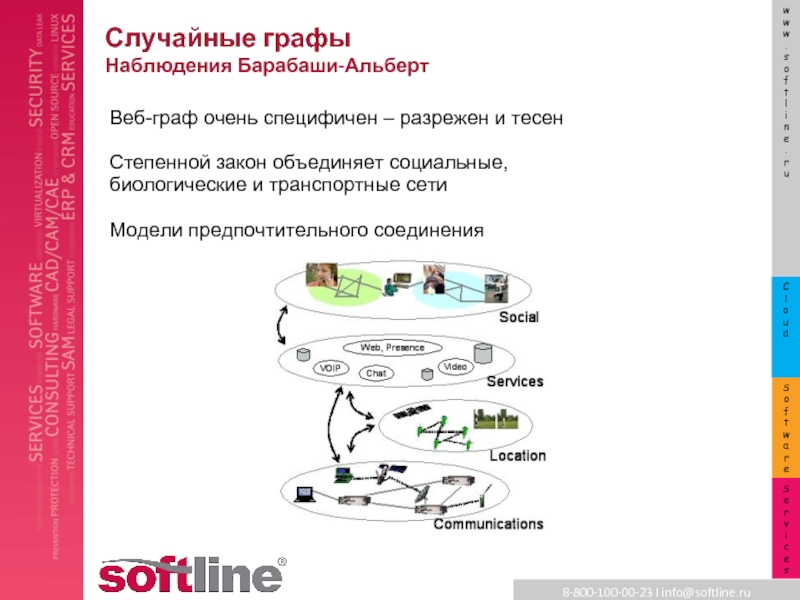
Слайд 19Случайные графы
Наблюдения Барабаши-Альберт
Веб-граф очень специфичен – разрежен и тесен
Степенной закон объединяет
социальные, биологические и транспортные сети
Модели предпочтительного соединения
Модели предпочтительного соединения
Слайд 20Случайные графы
Модель Эрдёша-Реньи
G(n,p)
V = {1, 2, …, n}, E
рёбра проводятся взаимно-независимо
с
вероятностью p ∈ [0, 1] в соответствии со
схемой Бернулли
e1, …, em, m = C2n – количество всех испытаний
Вероятностное пространство <Ωn, Fn, Pn,p>
Ωn = {G = (Vn, E)} – множество элементарных событий
Fn = 2Ωn – множество событий
Pn,p(G) = p|E|(1-p)m-|E| - вероятность повления конкретного графа
вероятностью p ∈ [0, 1] в соответствии со
схемой Бернулли
e1, …, em, m = C2n – количество всех испытаний
Вероятностное пространство <Ωn, Fn, Pn,p>
Ωn = {G = (Vn, E)} – множество элементарных событий
Fn = 2Ωn – множество событий
Pn,p(G) = p|E|(1-p)m-|E| - вероятность повления конкретного графа
Слайд 23Highway dimension
Почему современные алгоритмы на картах работают очень быстро
100000 млн вершин
Время
работы 10-2 c
Интуитивные идеи:
Указатели на дугах
Поиск A*
Достижимость
Шоссейная и желаемые иерархии
Перевалочные пункты
Интуитивные идеи:
Указатели на дугах
Поиск A*
Достижимость
Шоссейная и желаемые иерархии
Перевалочные пункты
Слайд 27P vs NP
Задача поиска задаётся алгоритмом C, который получает на вход
условие I и кандидата на решение S и имеет полиномиальное, относительно I время работы.
S называется решением если и только если C(S, I) = true
NP – класс всех задач поиска, решение для которых может быть быстро проверено
P – класс задач поиска, решение для которых может быть быстро найдено
P ≠ NP – верно ли, что каждый раз, когда решение можно быстро проверить, его можно быстро найти
Задача о расписании
Задача о вершинном покрытии
A → B
S называется решением если и только если C(S, I) = true
NP – класс всех задач поиска, решение для которых может быть быстро проверено
P – класс задач поиска, решение для которых может быть быстро найдено
P ≠ NP – верно ли, что каждый раз, когда решение можно быстро проверить, его можно быстро найти
Задача о расписании
Задача о вершинном покрытии
A → B
Слайд 30Что осталось нерассмотренным
Параллельные алгоритмы
Распознавание изображений
Нейронные сети
Генетические алгоритмы
Нечёткие модели
Строковые алгоритмы
Комбинаторная оптимизация
Численные алгоритмы
Вычислительная
геометрия
Криптографические алгоритмы
Компьютерная лингвистика
……..
Криптографические алгоритмы
Компьютерная лингвистика
……..
Слайд 31Так говорил Дейкстра
I think it wise, and only honest, to warn
you that my goal is immodest. It is not my purpose to "transfer knowledge" to you that, subsequently, you can forget again. My purpose is no less than to effectuate in each of you a noticeable, irreversable change. I want you to see and absorb calculational arguments so effective that you will never be able to forget that exposure. I want you to gain, for the rest of your lives, the insight that beautiful proofs are not "found" by trial and error but are the result of a consciously applied design discipline. I want to inspire you to raise your quality standards. I mean, if 10 years from now, when you are doing something quick and dirty, you suddenly visualize that I am looking over your shoulders and say to yourself "Dijkstra would not have liked this.", well, that would be enough immortality for me.