- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
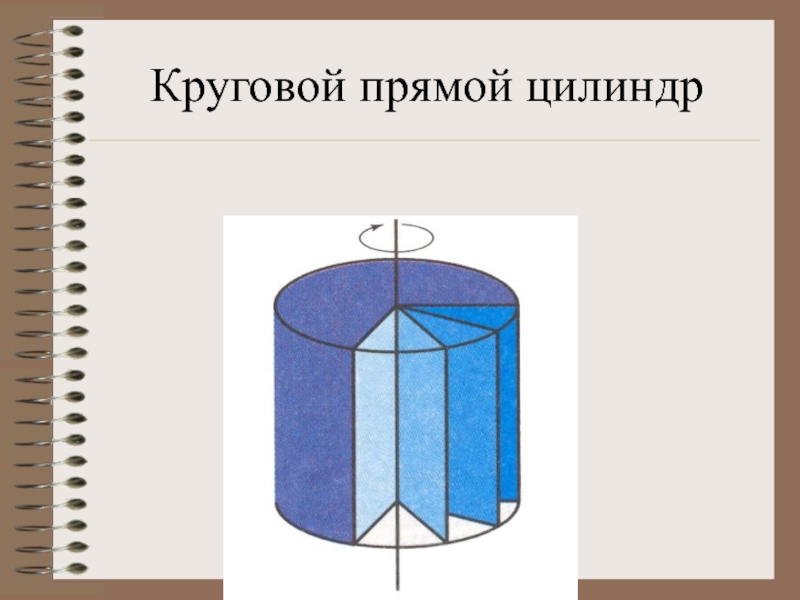
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОБЪЁМ. презентация
Содержание
- 1. ОБЪЁМ.
- 2. Положительная величина, характеризующая часть пространства, занимаемую телом, называется объемом тела. Определение:
- 3. Чтобы найти объём многогранника, нужно разбить его
- 4. Общие свойства объемов тел:
- 5. Рассмотрим первое свойство. за единицу объема
- 6. равные тела имеют равные объемы, при перемещении
- 7. Рассмотрим третье свойство. если тело разбить на
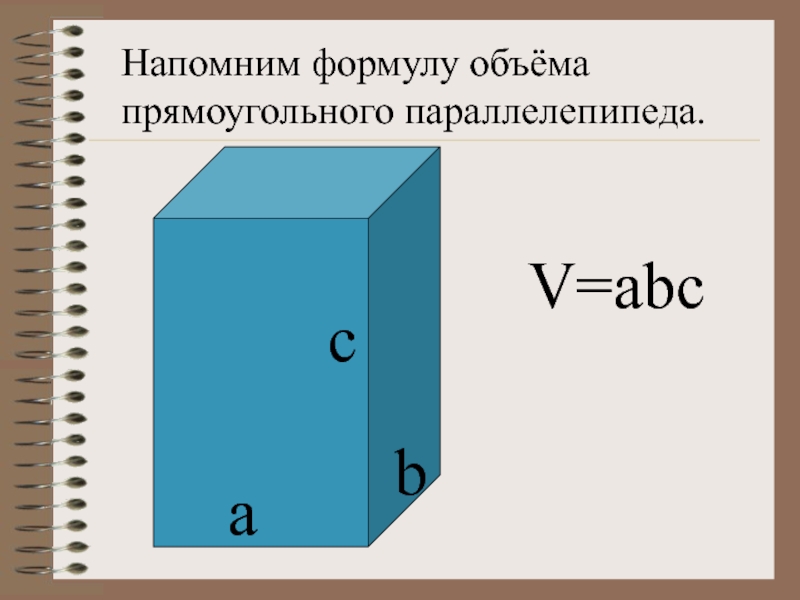
- 8. с а b V=abc Напомним формулу объёма прямоугольного параллелепипеда.
- 9. Как же найти объём произвольной призмы? Если
- 10. Рассмотрим произвольную прямую треугольную призму ABCA1B1C1. Если
- 11. Докажем, что объём прямой треугольной призмы, в
- 12. V=abc:2 V=Sc V=Sh
- 13. Существуют так же и наклонные призмы, объём
- 14. Как и любые другие тела, многогранники имеют
- 15. Понятие цилиндра.
- 16. ЦИЛИНДР Если в одной из
- 17. Цилиндры вокруг нас.
- 18. Цилиндрическая поверхность. Если в одной
- 19. Точное название определенного выше тела – прямой
- 20. Цилиндры бывают прямыми и наклонными в зависимости
- 21. Высота, радиус и ось цилиндра.
- 22. Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра, радиус которого равен 2. 4
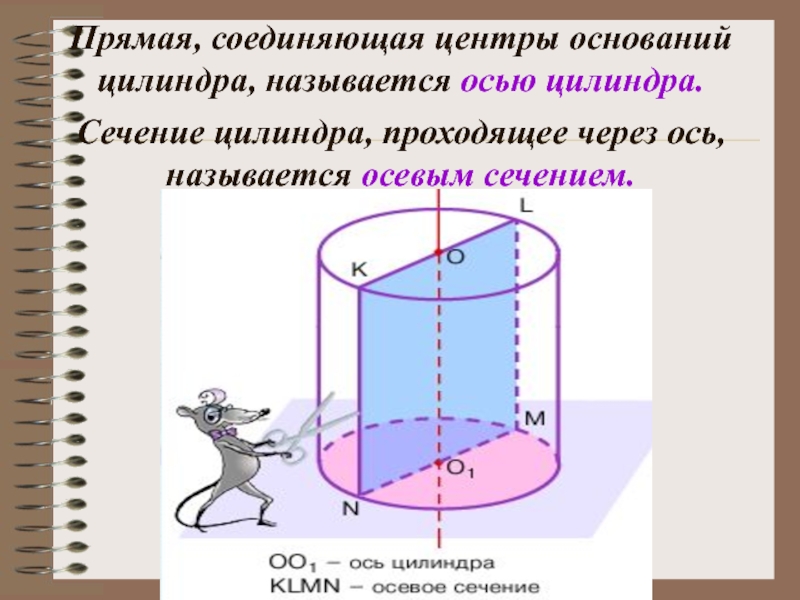
- 23. Прямая, соединяющая центры оснований цилиндра, называется осью
- 24. Найдите площадь осевого сечения цилиндра, если известны радиус его основания и высота. 20
- 25. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси.
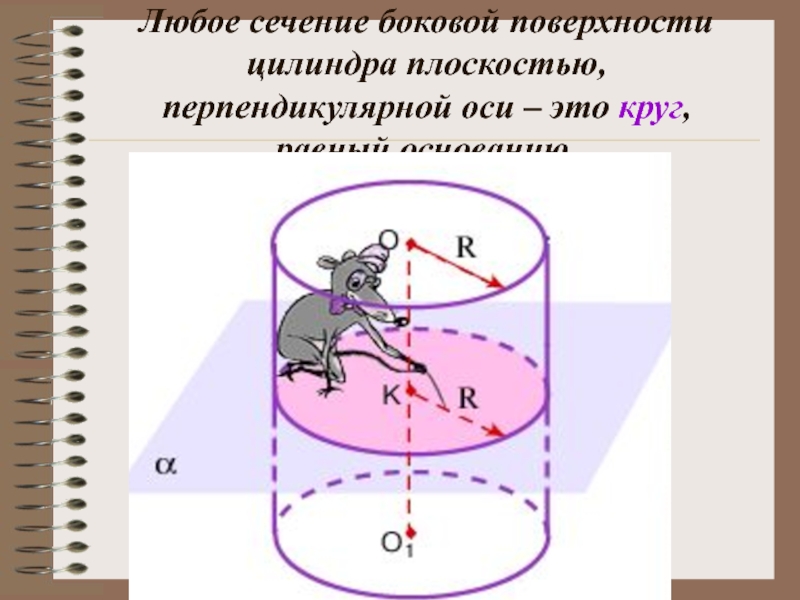
- 26. Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг, равный основанию.
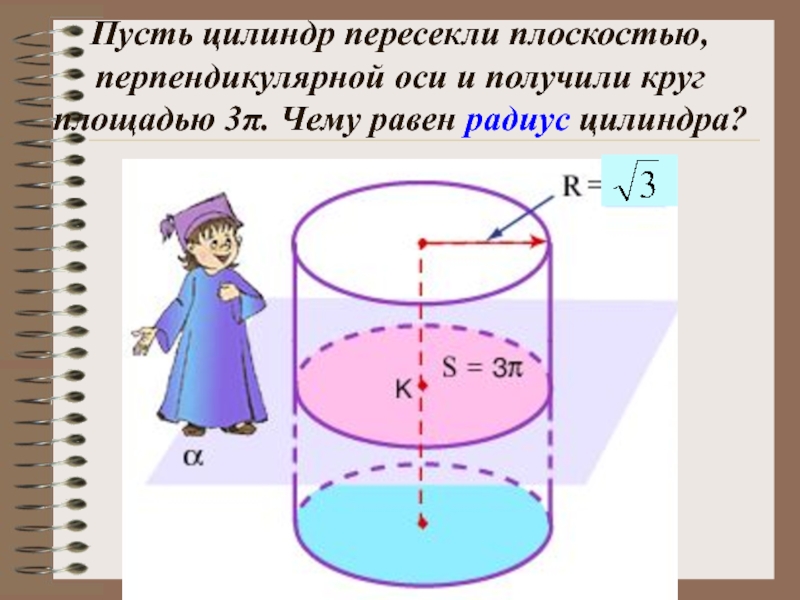
- 27. Пусть цилиндр пересекли плоскостью, перпендикулярной оси и
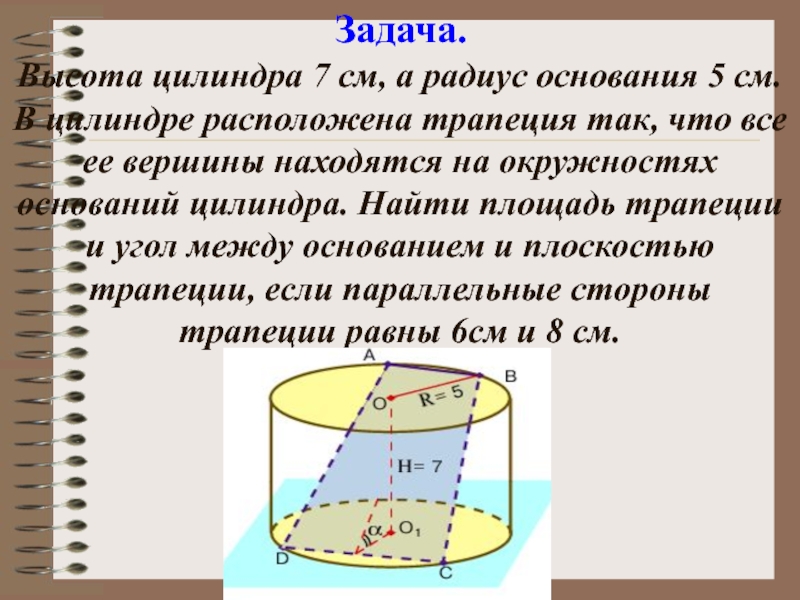
- 28. Высота цилиндра 7 см, а радиус основания
- 29. Цилиндр Определение. Тело,
- 30. Круговой прямой цилиндр
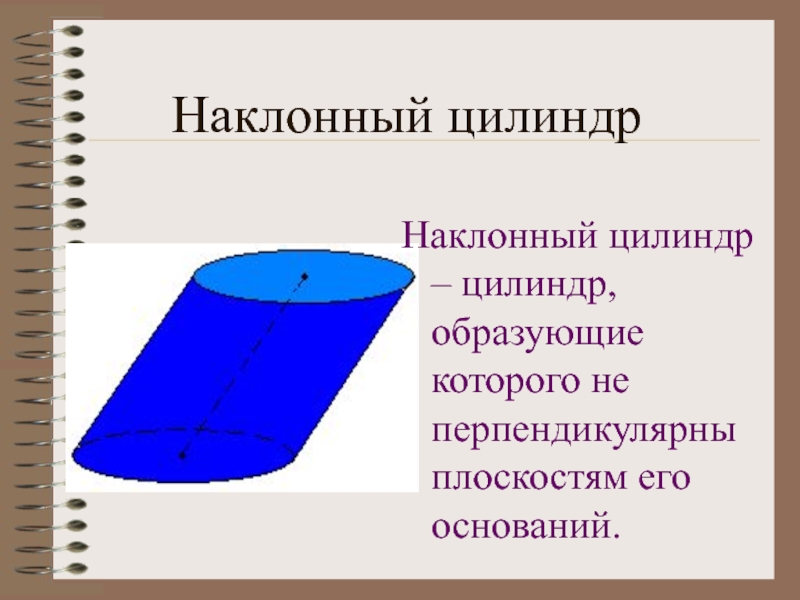
- 31. Наклонный цилиндр Наклонный цилиндр – цилиндр, образующие которого не перпендикулярны плоскостям его оснований.
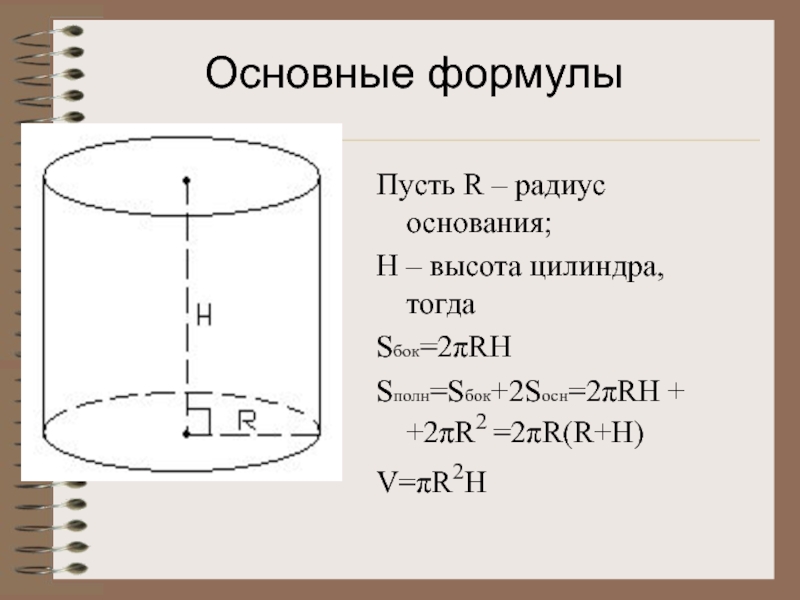
- 32. Пусть R – радиус основания; H
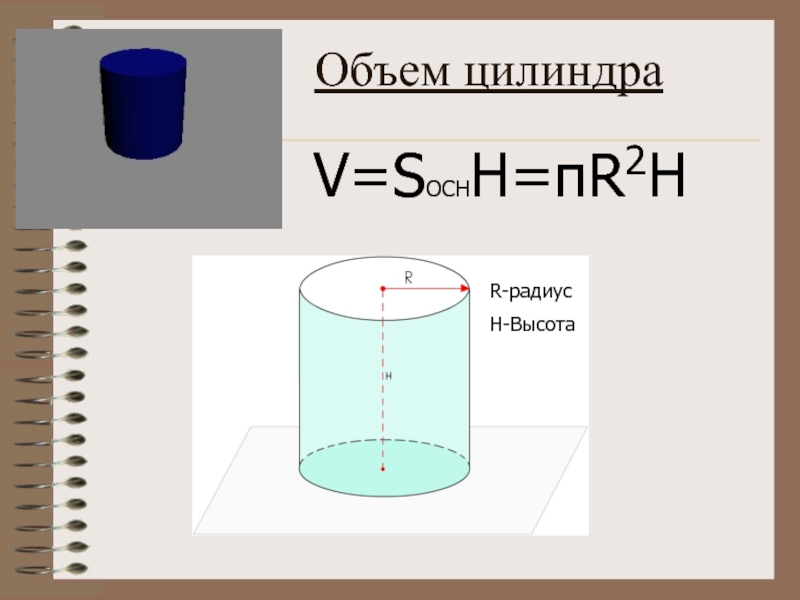
- 33. Объем цилиндра V=SОСНH=πR2H R-радиус H-Высота
Слайд 1ОБЪЁМ.
ЦЕЛИ УРОКА:
Усвоить понятие объёма многогранника;
Запомнить основные свойства объёма;
Узнать формулу объёма призмы.
Слайд 2Положительная величина, характеризующая часть пространства, занимаемую телом, называется объемом тела.
Определение:
Слайд 3Чтобы найти объём многогранника, нужно разбить его на кубы с ребром,
равным единице измерения.
V=20ед.3
Слайд 4Общие свойства объемов тел:
1) за единицу объема
принят объем куба, ребро которого равно единице длины;
2) равные тела имеют равные объемы, при перемещении тела его объем не изменяется;
3) если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей.
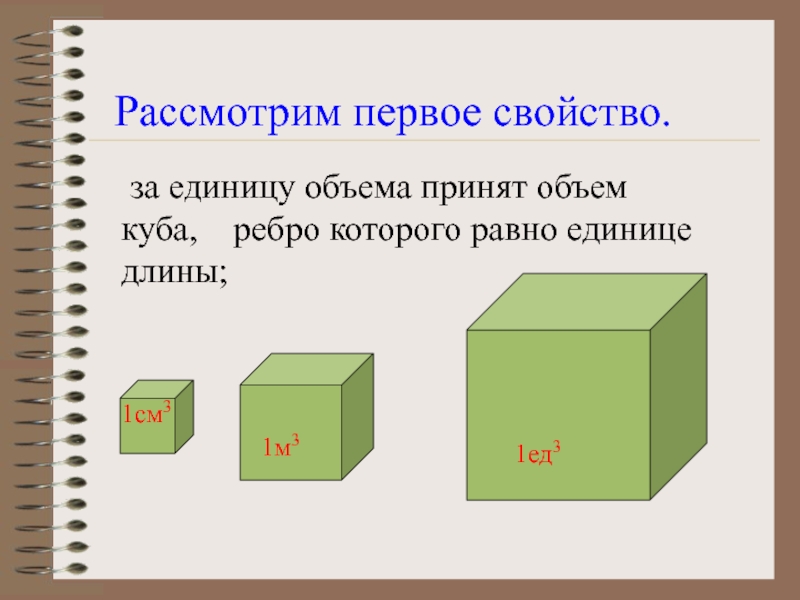
Слайд 5Рассмотрим первое свойство.
за единицу объема принят объем куба, ребро
которого равно единице длины;
1см3
1м3
1ед3
Слайд 6равные тела имеют равные объемы, при перемещении тела его объем не
изменяется;
Рассмотрим второе свойство.
V1
V2
V1= V2
Слайд 7Рассмотрим третье свойство.
если тело разбить на части, являющиеся простыми телами, то
объем тела равен объему его частей.
Слайд 9Как же найти объём произвольной призмы?
Если есть прямая n - угольная
призма (n>3), разобьем ее на конечное число прямых треугольных призм. Сложив объемы этих треугольных призм, получим объем n - угольной призмы.
Ф1
Ф2
Ф3
V=V1 +V2 +V3
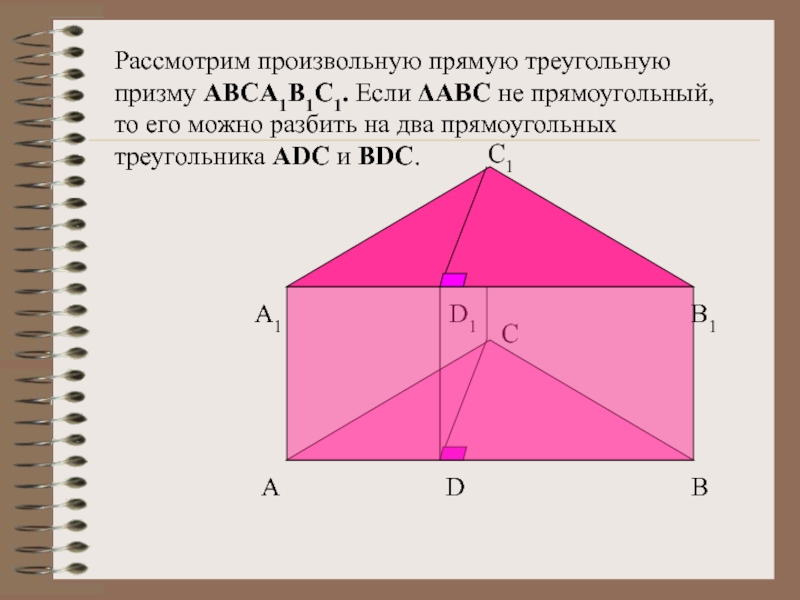
Слайд 10Рассмотрим произвольную прямую треугольную призму ABCA1B1C1. Если ΔABC не прямоугольный, то
его можно разбить на два прямоугольных треугольника ADC и BDC.
A D B
A1 D1 B1
C1
C
Слайд 11Докажем, что объём прямой треугольной призмы, в основании, которой прямоугольный треугольник
равен произведению площади основания на высоту.
V=abc
V=abc
:2
:2
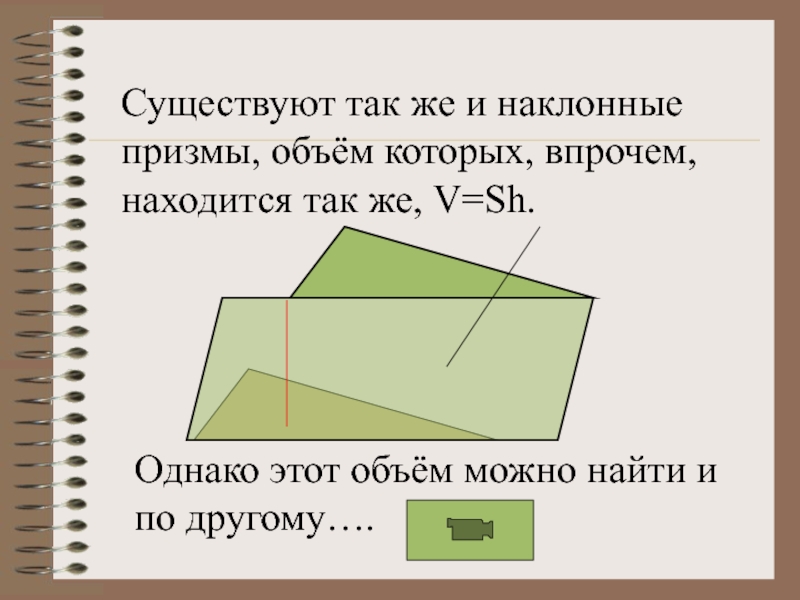
Слайд 13Существуют так же и наклонные призмы, объём которых, впрочем, находится так
же, V=Sh.
Однако этот объём можно найти и по другому….
Слайд 14Как и любые другие тела, многогранники имеют ОБЪЁМ!
Его можно измерить с
помощью выбранной единицы измерения объёма:
кубический сантиметр (см3)
кубический метр (м3)
кубический миллиметр (мм3)
и т.д.
кубический сантиметр (см3)
кубический метр (м3)
кубический миллиметр (мм3)
и т.д.
Слайд 16ЦИЛИНДР
Если в одной из 2 параллельных плоскостей взять окружность,
и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров, это тело называется цилиндром.
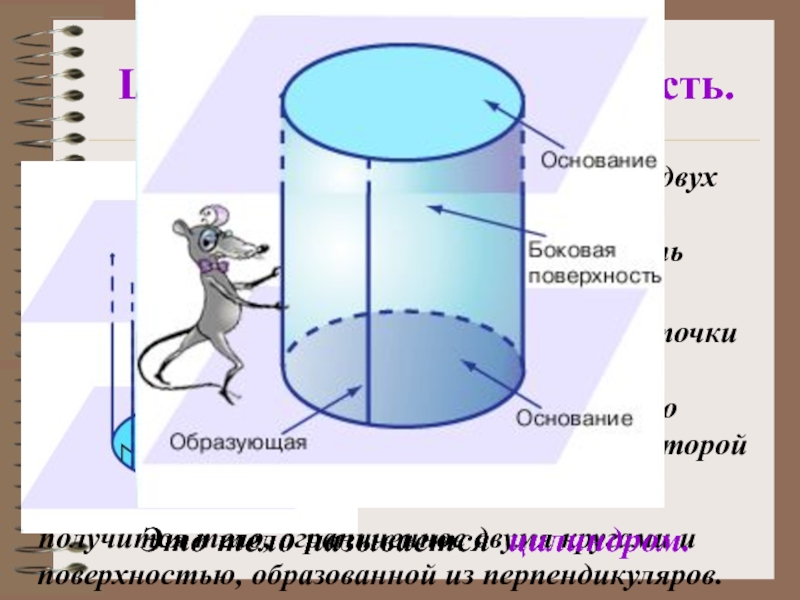
Слайд 18Цилиндрическая поверхность.
Если в одной из двух параллельных плоскостей взять
окружность,
и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то
и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то
получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров.
Это тело называется цилиндром.
Слайд 19Точное название определенного выше тела – прямой круговой цилиндр.
Вообще,
цилиндр возникает при пересечении цилиндрической поверхности, образованной множеством параллельных прямых, проведенных через каждую точку замкнутой кривой линии, и двух параллельных плоскостей.
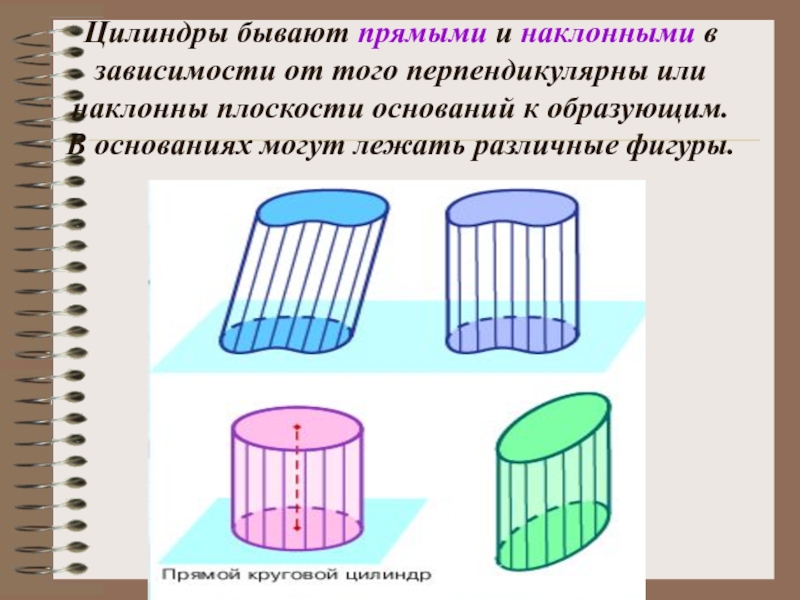
Слайд 20Цилиндры бывают прямыми и наклонными в зависимости от того перпендикулярны или
наклонны плоскости оснований к образующим.
В основаниях могут лежать различные фигуры.
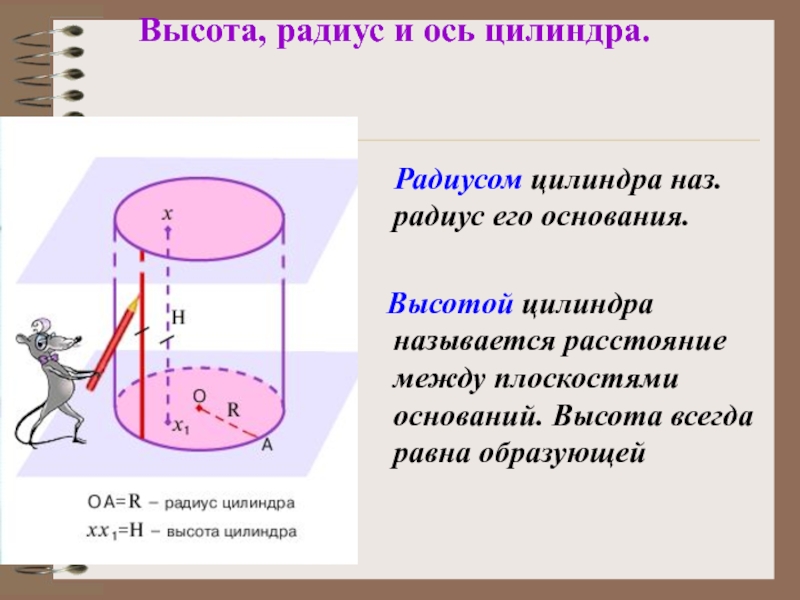
Слайд 21Высота, радиус и ось цилиндра.
Радиусом цилиндра наз. радиус его
основания.
Высотой цилиндра называется расстояние между плоскостями оснований. Высота всегда равна образующей
Высотой цилиндра называется расстояние между плоскостями оснований. Высота всегда равна образующей
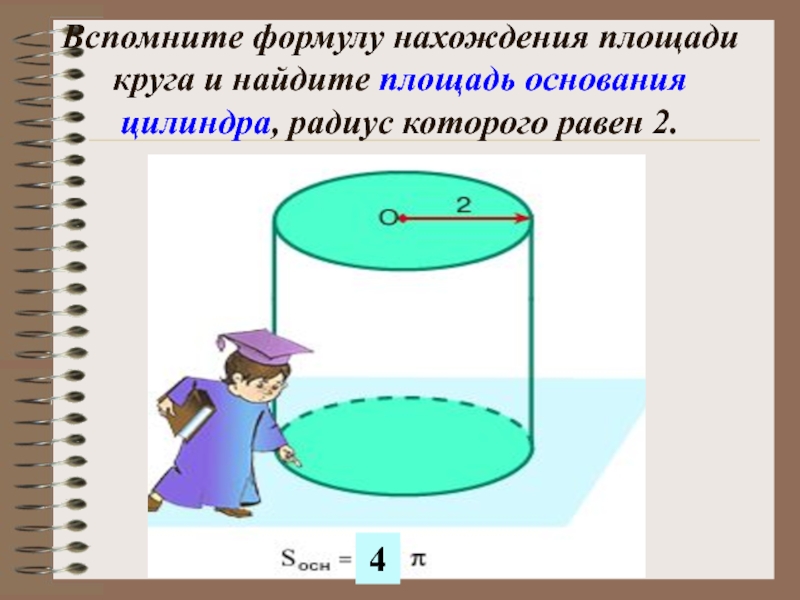
Слайд 22Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра, радиус
которого равен 2.
4
Слайд 23Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра.
Сечение цилиндра, проходящее через
ось, называется осевым сечением.
Слайд 25Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его
стороны как оси.
Слайд 26Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг,
равный основанию.
Слайд 27Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3π.
Чему равен радиус цилиндра?
Слайд 28Высота цилиндра 7 см, а радиус основания 5 см. В цилиндре
расположена трапеция так, что все ее вершины находятся на окружностях оснований цилиндра. Найти площадь трапеции и угол между основанием и плоскостью трапеции, если параллельные стороны трапеции равны 6см и 8 см.
Задача.
Слайд 29Цилиндр
Определение.
Тело, которое образуется при вращении прямоугольника вокруг
прямой, содержащей его сторону, называется цилиндром.
Слайд 31Наклонный цилиндр
Наклонный цилиндр – цилиндр, образующие которого не перпендикулярны плоскостям его
оснований.
Слайд 32Пусть R – радиус основания;
H – высота цилиндра, тогда
Sбок=2πRH
Sполн=Sбок+2Sосн=2πRH +
+2πR2 =2πR(R+H)
V=πR2H
V=πR2H
Основные формулы
