- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Некоторые вопросы моделирования морских экосистем презентация
Содержание
- 1. Некоторые вопросы моделирования морских экосистем
- 2. Определение модели по А. А. Ляпунову: Моделирование — это
- 3. При рассмотрении моделей сосредоточим наше внимание
- 4. Задача: изучить структуру сообществ макробентоса Каркинитского
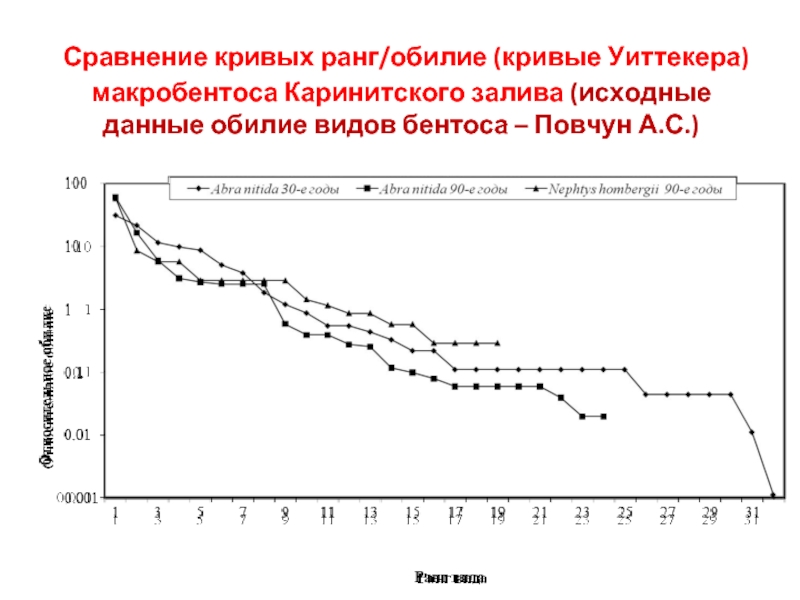
- 6. Сравнение кривых ранг/обилие (кривые Уиттекера) макробентоса
- 7. Глубоководный бентос, представленный в 30-е годы сообществом
- 8. Несколько менее общее определение математической модели, основанное
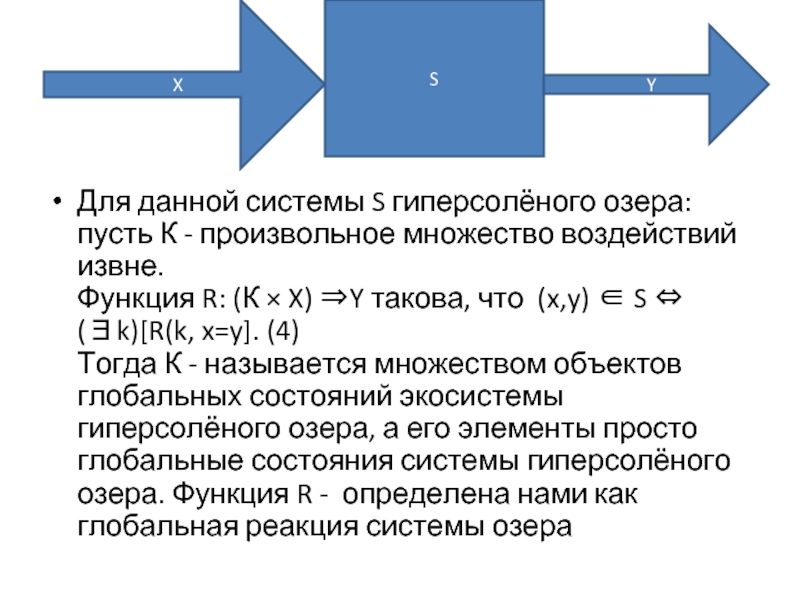
- 10. Для данной системы S гиперсолёного озера:
- 11. Исходные данные Макрофиты озера морского происхождения, расположенного
- 12. Модель поддерживающей ёмкости экосистемы гиперсолёного озера (данные-Prazukin, et al. 2008).
- 13. Модель = =Уравнение=Уравнение, выражающее идею.
- 14. Lt =27,25 (1-e- 0.609 ( t+0,143))
- 15. Оценить продолжительность жизни по расчетным показателям, вычисленным
- 16. Lt =27.25(1-e- 0.609 (t+0.143)) T = - [ln (1-Lm/L∞)] / К
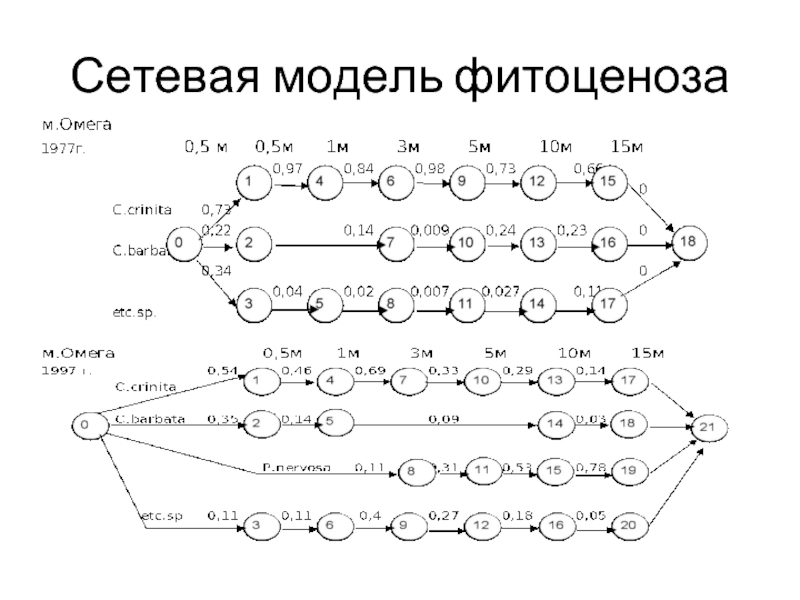
- 17. Сетевая модель фитоценоза (исходные данные -
- 18. Сетевая модель фитоценоза
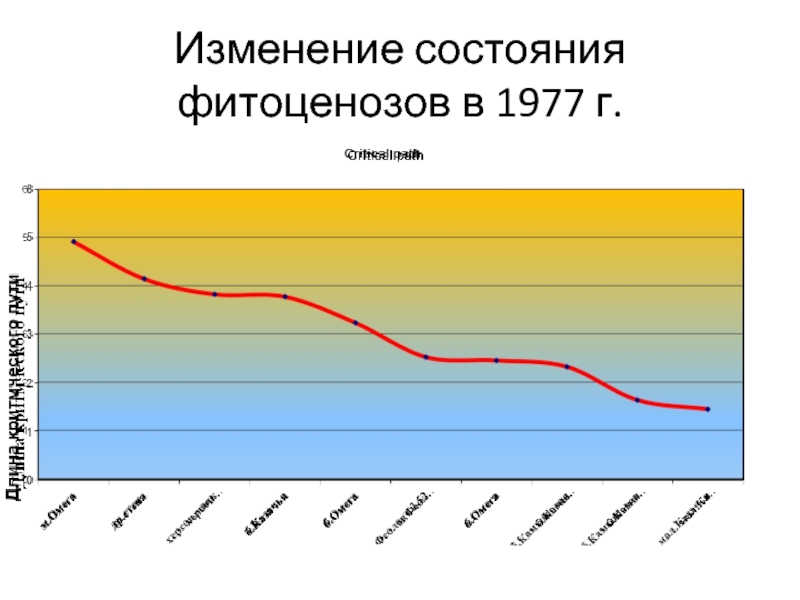
- 19. Изменение состояния фитоценозов в 1977 г.
- 20. Результатом оказалось то, что величины оценочных характеристик
- 21. Задачи математического моделирования Существует два основных класса
- 22. Основные этапы математического моделирования Построение модели. Решение
- 23. Построение модели. На этом этапе задается некоторый
- 24. Решение математической задачи, к которой приводит модель
- 25. Интерпретация полученных следствий из математической модели Следствия,
- 26. Проверка адекватности модели. На этом этапе выясняется,
- 27. Модификация модели. На этом этапе происходит либо
- 28. Классификация моделей (по характеру решаемых проблем)
- 29. Структурные модели Модель характеризует структуру сложного объекта,
- 30. Классификация моделей (по характеру исходных данных
- 31. Гипотетические модели Наиболее просто строится модель, когда
- 32. Заключение Построение математической модели в прикладных задачах
Слайд 2
Определение модели по А. А. Ляпунову: Моделирование — это опосредованное практическое или теоретическое исследование
объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель)
Слайд 3
При рассмотрении моделей сосредоточим наше внимание на
Постановке задачи
Входных параметрах
Модели
Результатах
Слайд 4Задача: изучить структуру сообществ
макробентоса Каркинитского залива в XX веке
находящаяся в
некотором объективном соответствии с познаваемым объектом;
способная замещать его в определенных отношениях;
дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.
способная замещать его в определенных отношениях;
дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.
Слайд 6 Сравнение кривых ранг/обилие (кривые Уиттекера) макробентоса Каринитского залива (исходные данные
обилие видов бентоса – Повчун А.С.)
Слайд 7Глубоководный бентос, представленный в 30-е годы сообществом двустворчатого моллюска Abra nitida
отличала устойчивая структура.
В 90-х годах сообщество Abra nitida смещается на северо-запад залива, а его место занимает сообщество полихеты Nephtys hombergii. Структура сообщества Abra nitida трансформируется.
В конце столетия структура глубоководного бентоса упрощена, что характерно для биотопов со средним уровня загрязнения.
В 90-х годах сообщество Abra nitida смещается на северо-запад залива, а его место занимает сообщество полихеты Nephtys hombergii. Структура сообщества Abra nitida трансформируется.
В конце столетия структура глубоководного бентоса упрощена, что характерно для биотопов со средним уровня загрязнения.
Слайд 8Несколько менее общее определение математической модели, основанное на идеализации «вход — выход —
состояние»
: Абстрактное математическое представление процесса, происходящего в биотопе, использует набор переменных, чтобы представлять входы, выходы и внутренние состояния.
В общем случае математическая модель реального объекта, процесса или системы представляется в виде системы функционалов
Фi (X,Y,Z,t)=0,
где X - вектор входных переменных, X=[x1,x2,x3, ... , xN]t,
Y - вектор выходных переменных, Y=[y1,y2,y3, ... , yN]t,
К - вектор внешних воздействий,
t - координата времени.
: Абстрактное математическое представление процесса, происходящего в биотопе, использует набор переменных, чтобы представлять входы, выходы и внутренние состояния.
В общем случае математическая модель реального объекта, процесса или системы представляется в виде системы функционалов
Фi (X,Y,Z,t)=0,
где X - вектор входных переменных, X=[x1,x2,x3, ... , xN]t,
Y - вектор выходных переменных, Y=[y1,y2,y3, ... , yN]t,
К - вектор внешних воздействий,
t - координата времени.
Слайд 10
Для данной системы S гиперсолёного озера: пусть К - произвольное множество
воздействий извне.
Функция R: (К × X) ⇒Y такова, что (x,y) ∈ S ⇔ (∃k)[R(k, x=y]. (4)
Тогда К - называется множеством объектов глобальных состояний экосистемы гиперсолёного озера, а его элементы просто глобальные состояния системы гиперсолёного озера. Функция R - определена нами как глобальная реакция системы озера
X
S
Y
Слайд 11Исходные данные
Макрофиты озера морского происхождения, расположенного вблизи черноморского мыса Херсонесский (г.
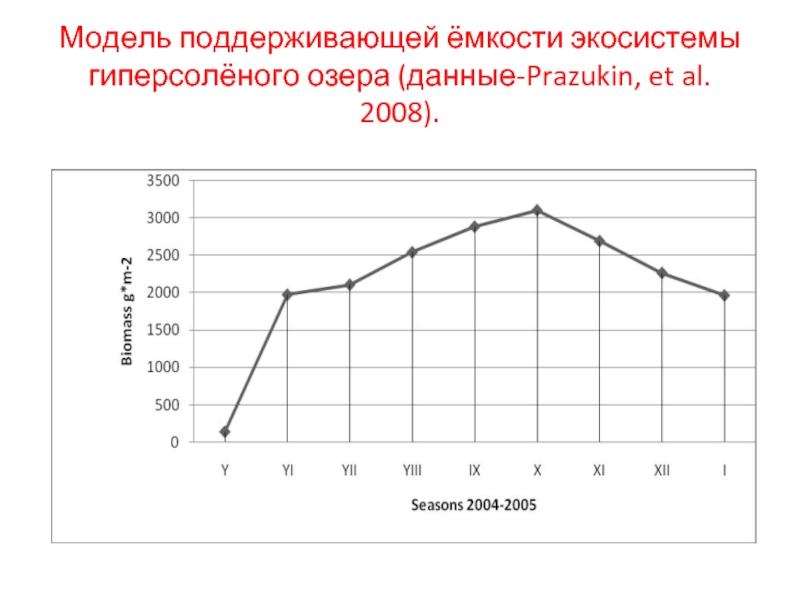
Севастополь). Исследование донной растительности озера показало, что в ее состав входят 4 вида, три из которых относятся к водорослям отдела Chlorophyta и один – к морским травам отдела Angiospermae. Зеленые водоросли представлены двумя родами (Cladophora Kütz. и Ulothrix Kütz.), двумя семействами (Ulothrichacea Kütz. и Cladophoracea Wille ) двух порядков (Chlorococcales Marchand и Cladophorales Haeckel). К зеленым водорослям озера относятся виды Cladophora vadorum (Aresch.) Kütz., C. siwachensis C. Meyer, Ulothrix implexa (Kütz.) Kütz. Из морских трав в озере встречен один вид - Ruppia cirrhosa (Petagna) Grande. Поддерживающая ёмкость расчитана в величинах средней фитомассы (г*м-2 ). На тренде, изменения поддерживающей ёмкости Херсонесского озера за исследуемый период отмечено два экстремума: максимум 3097,27 г*м-2 и минимум 137,39 г*м-2
Слайд 12Модель поддерживающей ёмкости экосистемы гиперсолёного озера (данные-Prazukin, et al. 2008).
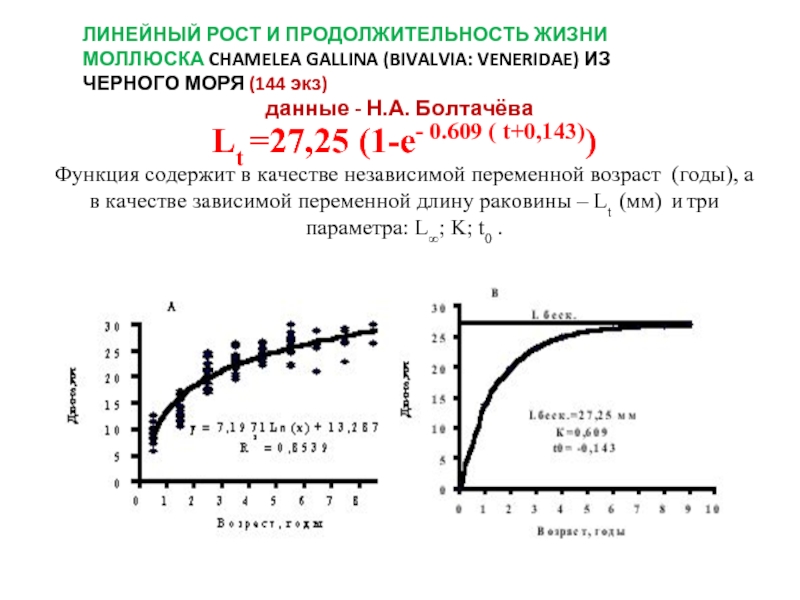
Слайд 14 Lt =27,25 (1-e- 0.609 ( t+0,143)) Функция содержит в качестве независимой переменной
возраст (годы), а в качестве зависимой переменной длину раковины – Lt (мм) и три параметра: L∞; K; t0 .
ЛИНЕЙНЫЙ РОСТ И ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ МОЛЛЮСКА CHAMELEA GALLINA (BIVALVIA: VENERIDAE) ИЗ ЧЕРНОГО МОРЯ (144 экз)
данные - Н.А. Болтачёва
Слайд 15Оценить продолжительность жизни по расчетным показателям, вычисленным на основании уравнения Берталанфи
T= -[ln(1-Lm/L∞)]/К,
где Т – возраст наиболее крупной особи, Lm - ее длина, К, L∞ - параметры уравнения Берталанфи, в качестве Lm - средний из максимальных размеров (например, из 7 измерений) равный 27,10 мм.
Полученный расчетный максимальный возраст равен максимальному возрасту моллюсков в исследованной выборке: 9 годам. Этот факт можно объяснить достаточно близким соответствием эмпирической и расчетной кривой
Интересен тот факт, что максимальный возраст, отмеченный для хамелеи из Средиземного моря – 4 года. Средний размер раковины для этой возрастной группы около 27 мм. Такого размера моллюски из Черного моря достигают в возрасте 8 лет
Разница в скорости роста одного и того же вида в разных частях ареала может быть вызвана разными температурными условиями обитания: 7 – 28 оС (Средиземное море, побережье Испании) и 4 - 21 оС (Черное море, бухта Омега)
Слайд 17Сетевая модель фитоценоза (исходные данные
- А.А. Калугина-Гутник - Н.А. Мильчакова)
Была
создана база данных на основе имеющихся материалов 1967,1977,1997гг. В базу вошли фитоценозы Севастопольских бухт и западного побережья Крыма. Построены сетевые модели цистозировых фитоценозов открытого берега. Херсонесский маяк, Древняя стена, м. Омега.
Слайд 20Результатом оказалось то, что величины оценочных характеристик моделей разбивают Севастопольские бухты
на ранжированный ряд, в котором меньшим величинам соответствуют бухты с наибольшей степенью загрязнения, а большим фитоценозы открытого берега. Согласно оценочным параметрам, сетевых моделей за 20 лет в фитоценозах Херсонессого маяка, м. Омега, в районе Херсонесского заповедника произошли структурные изменения свидетельствуют о перестройке структуры сообществ и уменьшении составляющей доминирующего видов C.crinita и C.barbata. Все отмеченные нами изменения в фитоценозах свидетельствуют об ухудшении состояния рассмотренных фитосообществ.
Слайд 21Задачи математического моделирования
Существует два основных класса задач, связанных с математическими моделями:
прямые и обратные. В первом случае все параметры модели считаются известными, и нам остается только исследовать её поведение (сетевая модель, стохастическая модель структуры сообщества)
Порой требуется решить обратную задачу: какие-то параметры модели неизвестны (например, не могут быть измерены явно), и требуется их найти, сопоставляя поведение реальной системы с её моделью (гиперсолёное озеро, модель роста)
Порой требуется решить обратную задачу: какие-то параметры модели неизвестны (например, не могут быть измерены явно), и требуется их найти, сопоставляя поведение реальной системы с её моделью (гиперсолёное озеро, модель роста)
Слайд 22Основные этапы математического моделирования
Построение модели.
Решение математической задачи, к которой приводит модель.
Интерпретация
полученных следствий из математической модели.
Проверка адекватности модели.
Модификация модели
Проверка адекватности модели.
Модификация модели
Слайд 23Построение модели.
На этом этапе задается некоторый объект — e.g.- сообщество. При
этом, как правило, четкое описание ситуации затруднено.
Сначала выявляются основные особенности биотопа и связи между биотическими и абиотическими составляющими на качественном уровне.
Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.
Сначала выявляются основные особенности биотопа и связи между биотическими и абиотическими составляющими на качественном уровне.
Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.
Слайд 24Решение математической задачи, к которой приводит модель
На этом этапе большое внимание
уделяется разработке алгоритмов и численных методов решения задачи, при помощи которых результат может быть найден с необходимой точностью.
Слайд 25 Интерпретация полученных следствий из математической модели
Следствия, выведенные из модели на языке
математики, интерпретируются на языке, принятом в гидробиологии.
Слайд 26Проверка адекватности модели.
На этом этапе выясняется, согласуются ли результаты эксперимента с
теоретическими следствиями из модели в пределах определенной точности e.g.- в качестве примера может послужить сравнение в разнице в скорости роста одного и того же вида в разных частях ареала и обитания максимальный возраста, отмеченного для хамелеи из Чёрного и Средиземного морей
Слайд 27Модификация модели.
На этом этапе происходит либо усложнение модели, чтобы она была
более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.
Слайд 28Классификация моделей
(по характеру решаемых проблем)
Модели могут быть разделены на
функциональные и структурные.
Функциональные модели:
все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие — как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа.
Функциональные модели:
все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие — как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа.
Слайд 29Структурные модели
Модель характеризует структуру сложного объекта, состоящего из отдельных частей, между
которыми существуют определенные связи. Как правило, эти связи не поддаются количественному измерению. Для построения таких моделей удобно использовать теорию графов (сетевая модель фитоценоза).
Слайд 30Классификация моделей
(по характеру исходных данных и результатов предсказания )
Модели
могут быть разделены на детерминистические и вероятностно-статистические.
Модели детерминистические дают определенные, однозначные предсказания(уравнение роста).
Модели вероятностно-статистические основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер (структура глубоководного бентоса).
Модели детерминистические дают определенные, однозначные предсказания(уравнение роста).
Модели вероятностно-статистические основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер (структура глубоководного бентоса).
Слайд 31Гипотетические модели
Наиболее просто строится модель, когда хорошо известны законы, определяющие поведение
и свойства объекта, процесса или системы, и имеется большой практический опыт их применения.
Более сложная ситуация возникает тогда, когда наши знания об изучаемом объекте, процессе или системе недостаточны. В этом случае при построении математической модели приходится делать дополнительные предположения, которые носят характер гипотез, такая модель называется гипотетической.
Выводы, полученные в результате исследования такой гипотетической модели, носят условный характер
Более сложная ситуация возникает тогда, когда наши знания об изучаемом объекте, процессе или системе недостаточны. В этом случае при построении математической модели приходится делать дополнительные предположения, которые носят характер гипотез, такая модель называется гипотетической.
Выводы, полученные в результате исследования такой гипотетической модели, носят условный характер
Слайд 32Заключение
Построение математической модели в прикладных задачах гидробиологии – один из наиболее
сложных и ответственных этапов работы.
Опыт показывает, что во многих случаях правильно выбрать модель – значит решить проблему более, чем наполовину.
Трудность данного этапа состоит в том, что он требует соединения математических и специальных знаний. Поэтому очень важно, чтобы при решении прикладных задач математики обладали специальными знаниями об объекте, а их партнеры, специалисты, – определенной математической культурой, опытом исследования в своей области.
Опыт показывает, что во многих случаях правильно выбрать модель – значит решить проблему более, чем наполовину.
Трудность данного этапа состоит в том, что он требует соединения математических и специальных знаний. Поэтому очень важно, чтобы при решении прикладных задач математики обладали специальными знаниями об объекте, а их партнеры, специалисты, – определенной математической культурой, опытом исследования в своей области.










![Оценить продолжительность жизни по расчетным показателям, вычисленным на основании уравнения Берталанфи T= -[ln(1-Lm/L∞)]/К, где Т](/img/tmb/1/34327/d2e41e9a29986435c2f5a64b59e1b788-800x.jpg)
![Lt =27.25(1-e- 0.609 (t+0.143))T = - [ln (1-Lm/L∞)] / К](/img/tmb/1/34327/812ad458d8b73a7469eef74128c0a828-800x.jpg)