- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нахождение площади решётчатого многоугольника. презентация
Содержание
- 1. Нахождение площади решётчатого многоугольника.
- 2. Актуальность. Задачи на нахождение
- 3. Цель работы Поиск рационального способа решения данных задач.
- 4. Задание ЕГЭ 2012 года
- 5. Задание ЕГЭ 2012 года
- 6. Нахождение площади многоугольника с помощью формулы
- 7. Это соотношение открыл и
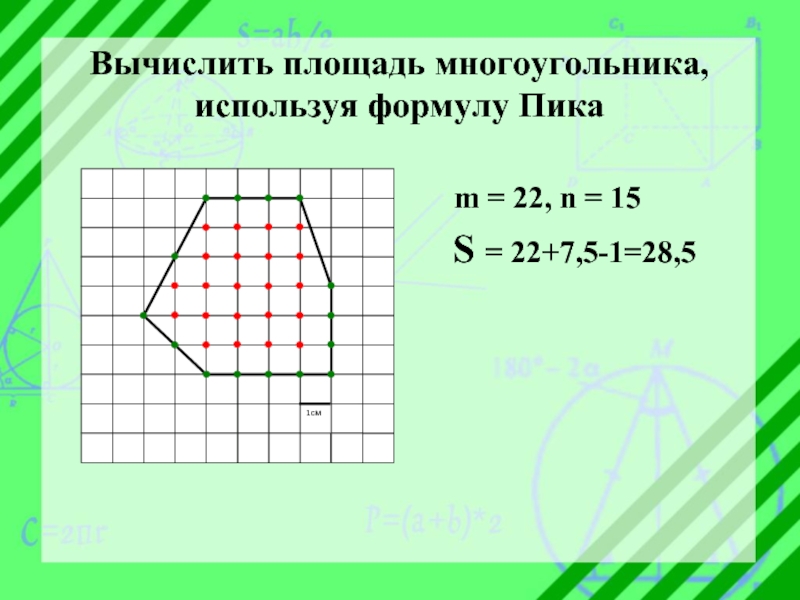
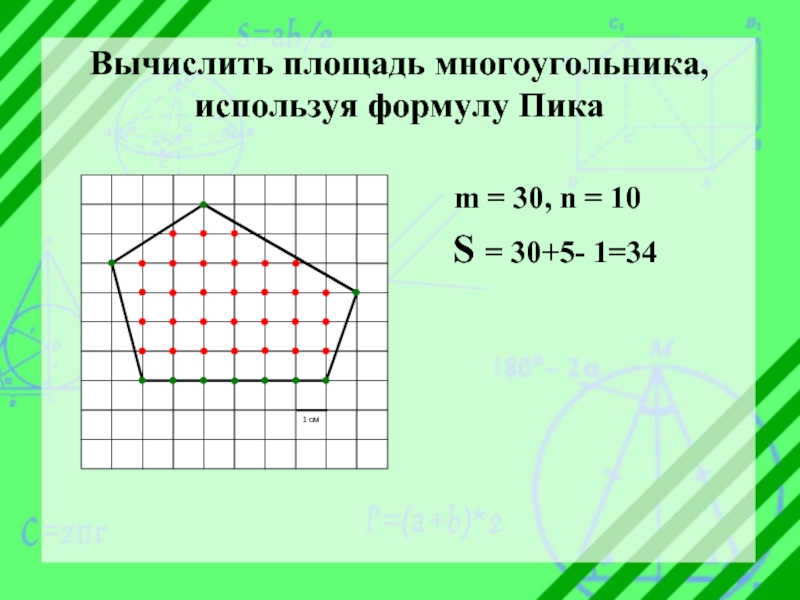
- 9. Вычислить площадь многоугольника, используя формулу Пика
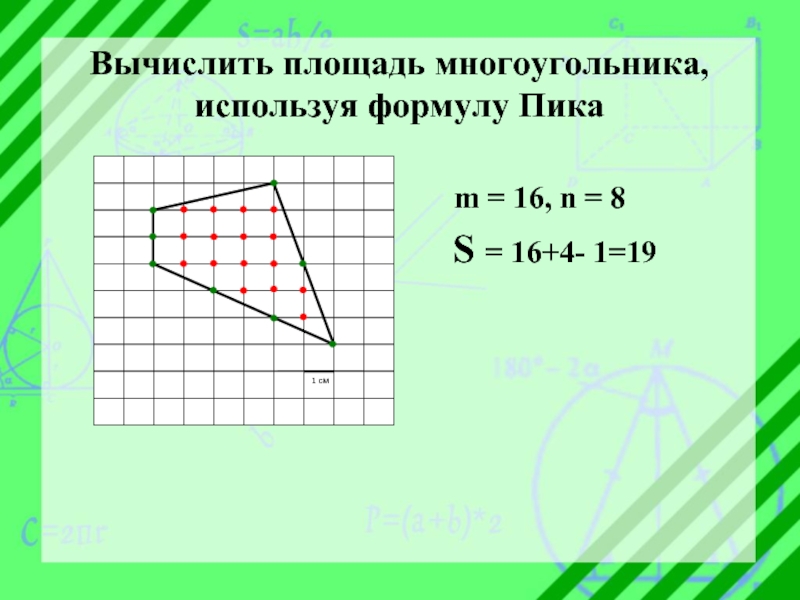
- 10. Вычислить площадь многоугольника, используя формулу Пика
- 11. Вычислить площадь многоугольника, используя формулу Пика
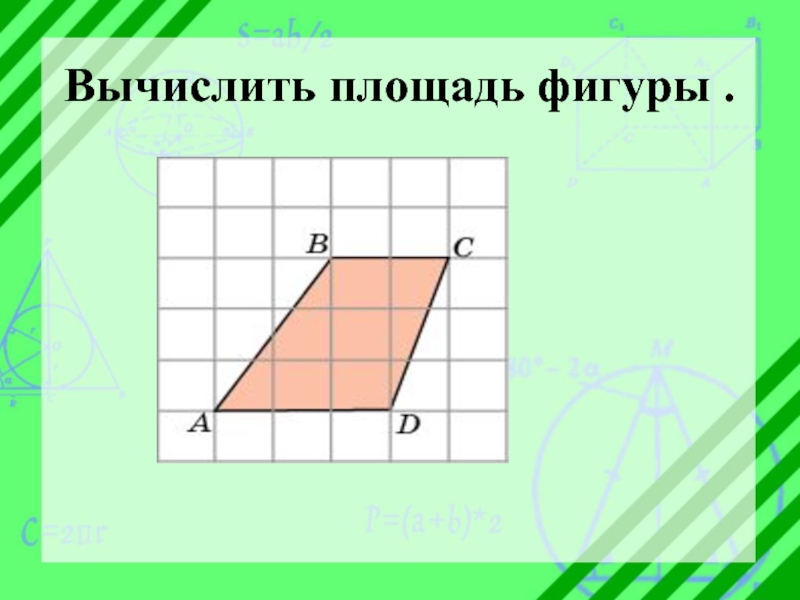
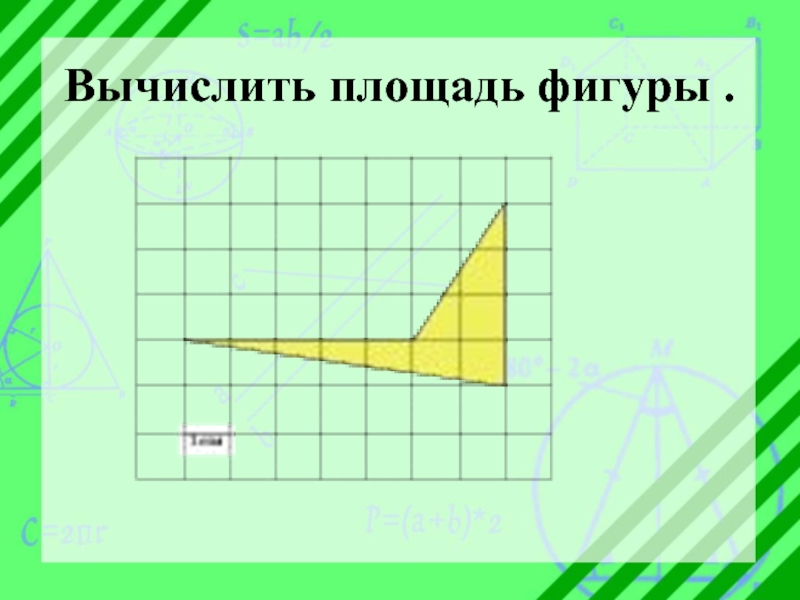
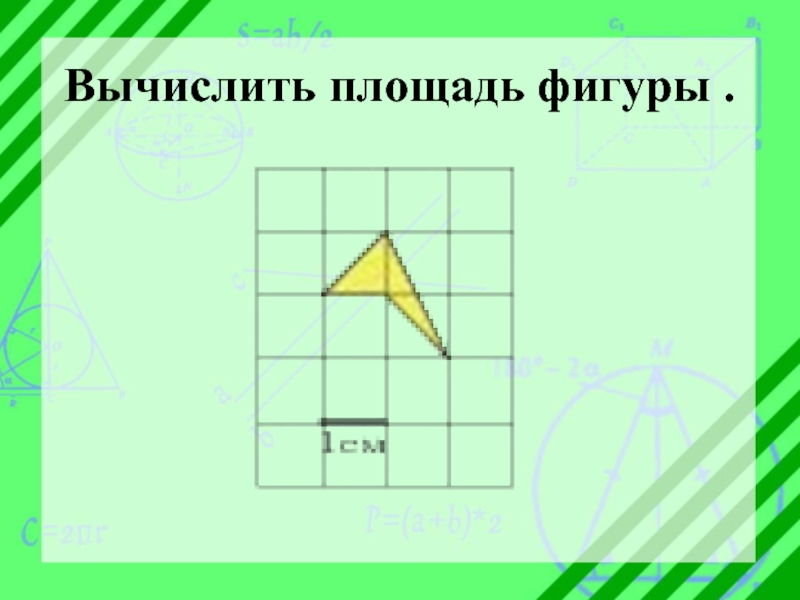
- 12. Вычислить площадь фигуры .
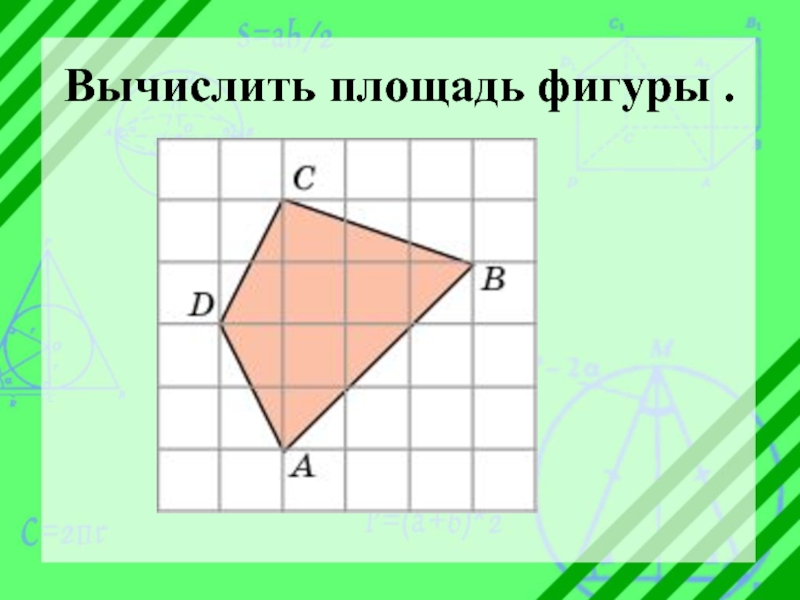
- 13. Вычислить площадь фигуры .
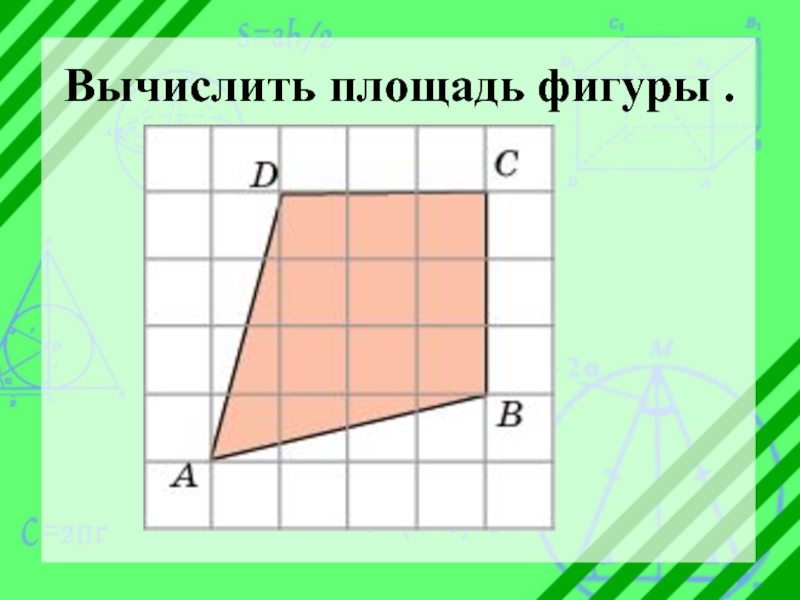
- 14. Вычислить площадь фигуры .
- 15. Вычислить площадь фигуры .
- 16. Вычислить площадь фигуры .
- 17. Вычислить площадь фигуры .
- 18. Вычислить площадь фигуры .
Слайд 2Актуальность.
Задачи на нахождение площадей решетчатых многоугольников часто встречаются на
ЕГЭ по математике.
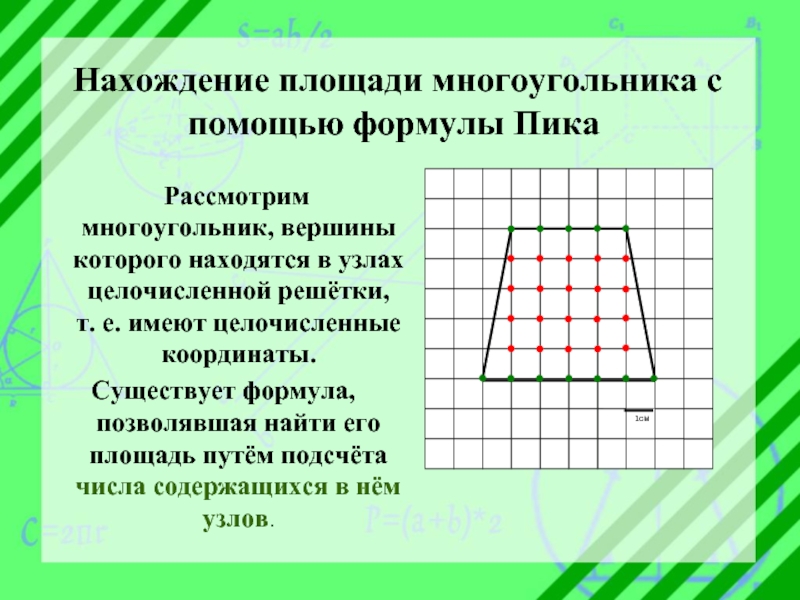
Слайд 6 Нахождение площади многоугольника с помощью формулы Пика
Рассмотрим
многоугольник, вершины которого находятся в узлах целочисленной решётки, т. е. имеют целочисленные координаты.
Существует формула, позволявшая найти его площадь путём подсчёта числа содержащихся в нём узлов.
Существует формула, позволявшая найти его площадь путём подсчёта числа содержащихся в нём узлов.
Слайд 7
Это соотношение открыл и доказал
австрийский математик
Георг Александр
Пик.
S = ( m + n/2 -1) ,
где m – колличество точек решетки
находящихся внутри многоугольника,
n – колличество точек решетки ,
лежащих на его
границе.
S = ( m + n/2 -1) ,
где m – колличество точек решетки
находящихся внутри многоугольника,
n – колличество точек решетки ,
лежащих на его
границе.
Слайд 8
Данная теорема не изучается в курсе
средней общеобразовательной школы.
Тем не менее , ее очень удобно использовать для решения задач на нахождение площадей решетчатого многоугольника.
Тем не менее , ее очень удобно использовать для решения задач на нахождение площадей решетчатого многоугольника.