- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МЫ ХОДИМ ПО ПЛОЩАДЯМ:КАК ИХ ИЗМЕРИТЬ? презентация
Содержание
- 1. МЫ ХОДИМ ПО ПЛОЩАДЯМ:КАК ИХ ИЗМЕРИТЬ?
- 2. ЦЕЛИ РАБОТЫ: уточнить понятие площади, выяснить историю
- 3. УТОЧНЕНИЕ ПОНЯТИЯ ПЛОЩАДИ Опр. 1. Фигура называется
- 4. ИСТОРИЯ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ Понятия площадей прямолинейных фигур
- 5. Основоположники геометрии. Математические труды.
- 6. Основоположники геометрии. Автор труда
- 7. Основоположники геометрии. Дал систематическое изложение основных
- 8. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ
- 9. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ
- 10. ВЫВОД ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА Нетрудно доказать, что
- 11. ВЫВОД ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА Тогда площадь произвольного
- 12. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ
- 13. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ
- 14. ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ
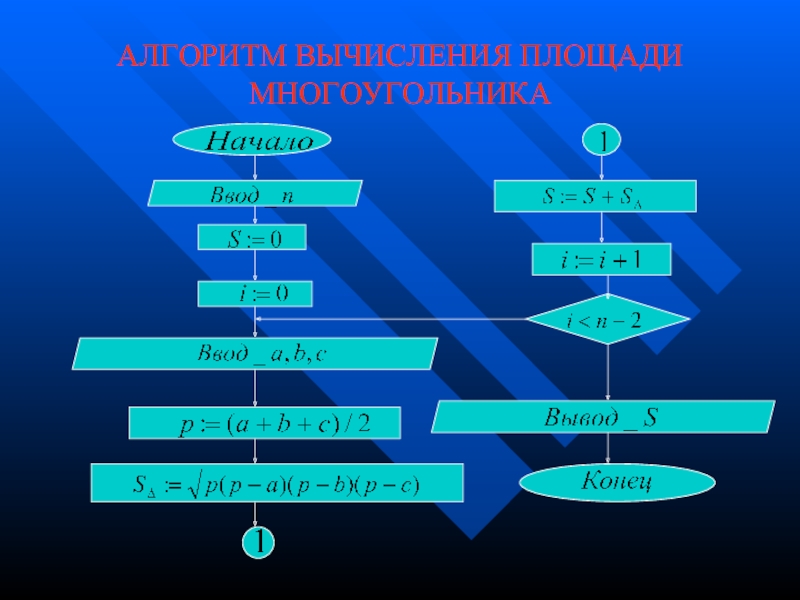
- 15. АЛГОРИТМ ВЫЧИСЛЕНИЯ ПЛОЩАДИ МНОГОУГОЛЬНИКА
- 16. ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ Треугольник
- 17. ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ Параллелограмм
- 18. ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ Трапеция
- 19. А КАК ПОСТУПИТЬ С КРУГОМ? Круг не
- 20. СЛЕДУЕТ ОТДАТЬ ДОЛЖНОЕ ДРЕВНЕГРЕЧЕСКИМ МАТЕМАТИКАМ!
- 21. МЫ ХОДИМ ПО ПЛОЩАДЯМ Над программой работали:
- 22. ИСТОЧНИКИ: материалы Internet, В.Д.Чистяков «Исторические экскурсы на
Слайд 1МЫ ХОДИМ ПО ПЛОЩАДЯМ:
КАК ИХ ИЗМЕРИТЬ?
Авторы: учащиеся 9 класса.
Copyright@Borisov&Maslova.Verchopenie.2004
Всем привет!
Слайд 2ЦЕЛИ РАБОТЫ:
уточнить понятие площади,
выяснить историю вопроса,
выстроить теорию «площади фигур» на основе
создать алгоритм вычисления площади многоугольника,
как поступить с кругом?
Слайд 3УТОЧНЕНИЕ ПОНЯТИЯ ПЛОЩАДИ
Опр. 1. Фигура называется простой, если она разбивается на
Опр. 2. Площадью простой фигуры называется неотрицательная ве-личина, обладающая следующи-ми свойствами:
Единицы площади:
Основные: 1 кв. см., 1 кв. м.;
Производные: 1 кв. мм., 1 кв. дм, 1ар, 1га, ...
1 ед.
1 кв. ед.
Слайд 4ИСТОРИЯ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ
Понятия площадей прямолинейных фигур (треугольника, прямоугольника, параллелограмма и трапеции)
Например, на папирусе Райнда приводится такая задача «Если тебе дан участок в поле с боковой стороной в 20 хет, с основаниями в 6 и 4 хет, то какова его площадь?» и ее решение:
½ ·(4+6)·20=100.
Слайд 5Основоположники геометрии.
Математические труды.
При доказательстве теорем о площадях
АРХИМЕД
ок. 287-212 до н. э.
- древнегреческий математик и механик
Слайд 6Основоположники геометрии.
Автор труда «Начала» в 13 книгах, в
ЕВКЛИД
конец IV-III в. до н. э.
- древнегреческий математик
- древнегреческий математик
Слайд 7Основоположники геометрии.
Дал систематическое изложение основных достижений античности в математике и
ГЕРОНА ФОРМУЛА - выражает площадь S треугольника через длины трех его сторон a, b и c и полупериметр p.
Точные даты рождения и смерти этого древнегреческого ученого и изобретателя из города Александрии неизвестны, поскольку арабские списки его трудов были переведены на современные языки только через 2000 лет после его смерти.
ГЕРОН
АЛЕКСАНДРИЙСКИЙ
около I века
- древнегреческий математик и механик
Слайд 8ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА
Поскольку фигура называется простой,
Слайд 9ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА
1. ВЫВОД ФОРМУЛЫ ПЛОЩАДИ
Так как площадь квадрата со стороной в 1 ед. равна S=1*1 кв. ед. (св-во 3),
то площадь прямоугольного треугольника с катетами 1 и 1 ед. будет равна S= ½*1*1 кв. ед. (св-во 2).
1 кв. ед.
S=1*1 кв. ед.
1 ед.
S=1/2*1*1 кв. ед.
1/2 кв. ед.
1 ед.
1 ед.
1 ед.
1 ед.
1 ед.
Слайд 10ВЫВОД ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА
Нетрудно доказать, что с увеличением одного из катетов
Тогда с увеличением другого катета полученного треугольника в b раз его площадь увеличится еще и в b раз и станет равной S=1/2*а*b кв. ед.
1 ед.
а ед.
S=1/2*а*1 кв. ед.
а ед.
b ед.
S=1/2*а*b кв. ед.
Слайд 11ВЫВОД ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА
Тогда площадь произвольного треугольника будет равна сумме площадей
Таким образом, площадь любого треугольника вычисляется по формуле
h
a1
a2
S1
S2
S = S1 + S2 =
= 1/2*a1*h + 1/2*a2*h =
= 1/2*(a1 + a2)*h = 1/2*a*h.
а
Слайд 12ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА
2. ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА равна
Таким образом,
И ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА, как частный случай параллелограмма, вычисляется по формуле:
h
а
S
S = 2*S1 = 2* 1/2ah = ah.
а
b
Слайд 13ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА
3. ПЛОЩАДЬ ТРАПЕЦИИ равна
Таким образом, площадь трапеции вычисляется по формуле:
а
b
h
S
S = 1/2*ah + 1/2*bh =
= 1/2*(a + b)h.
Слайд 14ПОСТРОЕНИЕ ТЕОРИИ «ПЛОЩАДИ ФИГУР» НА ОСНОВЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА
4. ПЛОЩАДЬ МНОГОУГОЛЬНИКА (выпуклого)
S
S
S
1
2
n-2
S
3
S = S + S + ... + S .
1
2
n-2
Слайд 16ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ
Треугольник
где a, b, c – стороны треугольника, р
Слайд 17ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ
Параллелограмм
Формулы площади ромба видоизменяются по
Ромб
Слайд 18ТАБЛИЦА ФОРМУЛ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ
Трапеция
Произвольный четырехугольник
где d – диагональ трапеции (четырехугольника).
Слайд 19А КАК ПОСТУПИТЬ С КРУГОМ?
Круг не является простой фигурой, поэтому формула
и его части: круговой сектор
и круговой сегмент
Слайд 21МЫ ХОДИМ ПО ПЛОЩАДЯМ
Над программой работали:
➢ 1-я гр. Понятие площади (Макаров А.).
➢ 2-я
➢ 3-я гр. Формулы площади четырехугольника (Прыгунов В., Мякотина Л., Ливадина М.).
➢ 4-я гр. Вычисление площади произвольного многоугольника (Поладов М., Киряева Ю., Демченко А.).
➢ 5-я гр. Формулы площади круга и его частей (Иванисова А., Избирян М.).
6-я гр. Основоположники теории площадей (Литвинов В., Кременева А., Шеховцова В.).
И УМЕЕМ ИХ ВЫЧИСЛЯТЬ!
Слайд 22ИСТОЧНИКИ:
материалы Internet,
В.Д.Чистяков «Исторические экскурсы на уроках математики в средней школе»,
Учебник по
А.И.Азевич «Задачи по геометрии. 7-9 классы. Дидактические материалы и контрольные работы.»