- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Молекулярная динамика(MD)лекция 2 презентация
Содержание
- 1. Молекулярная динамика(MD)лекция 2
- 2. Молекулярная механика Основы: Симуляции подчиняются законам
- 3. Уравнение Ньютона Fi Ковалентные взаимодействия Не ковалентные взаимодействия
- 4. Силовое поле, константы Константы из
- 5. Молекулярная динамика Сумма сил
- 6. Методология подготовки системы для МД Построение
- 7. Периодичные граничные условия МД поли-аланина показала
- 8. Что можно узнать из МД? равновесные свойства:
- 9. Ограничения МД Симуляции основаны на законе Ньютона
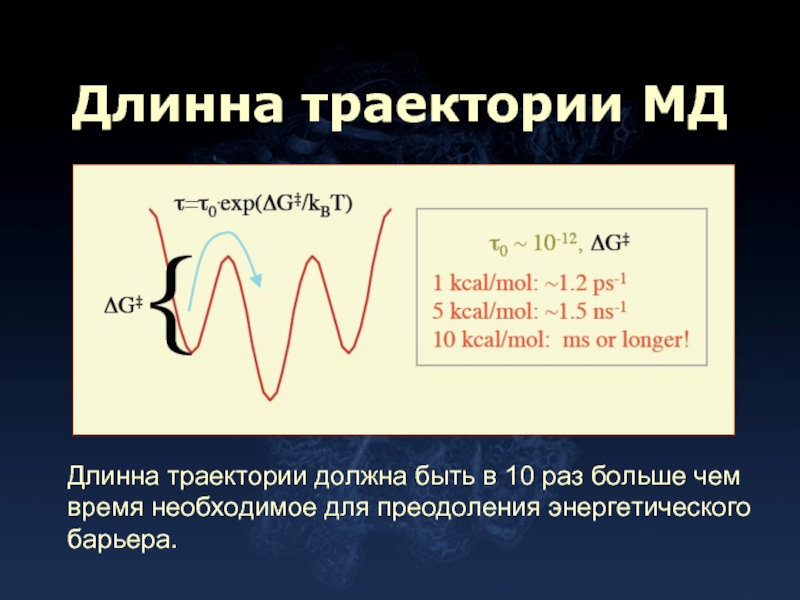
- 10. Длинна траектории МД Длинна траектории должна быть
- 11. Удаленные электростатические взаимодействия
- 12. Удаленные электростатические взаимодействия N2
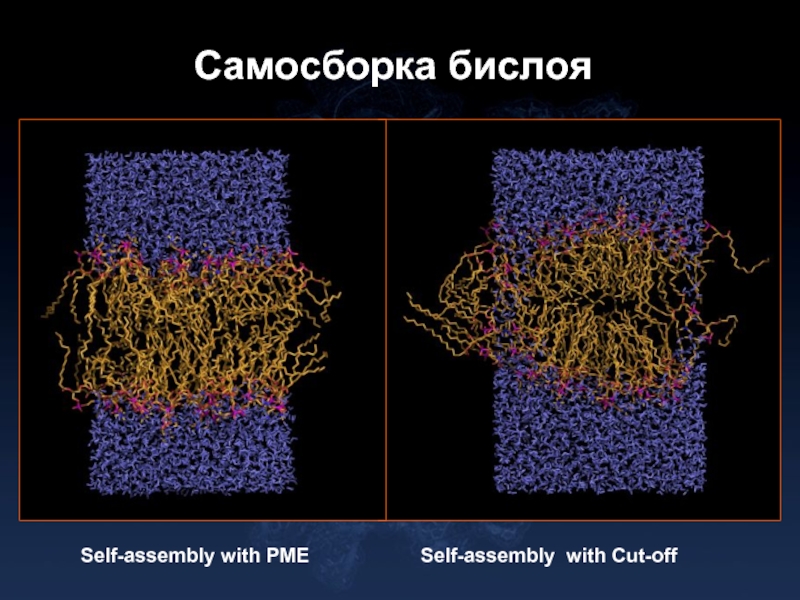
- 13. Самосборка бислоя Self-assembly with PME Self-assembly with Cut-off
- 14. Алгоритмы минимизации энергии системы hn максимальное
- 15. Алгоритмы минимизации энергии системы Conjugate Gradient
- 16. Алгоритмы минимизации энергии системы Очень эффективный
- 17. Увеличение шага интегратора МД Можно присвоить
- 18. Конструкции атомов-пустышек в GROMACS
- 19. МД с поляризацией (Shell MD) Используется
- 20. Стохастическая динамика Константа фрикции «Процесс шума» Используется при симуляции кристаллов
- 21. Броуновская динамика Коофицент фрикции «Процесс шума»
- 22. Анализ нормальных мод Выявление гармонических колебаний
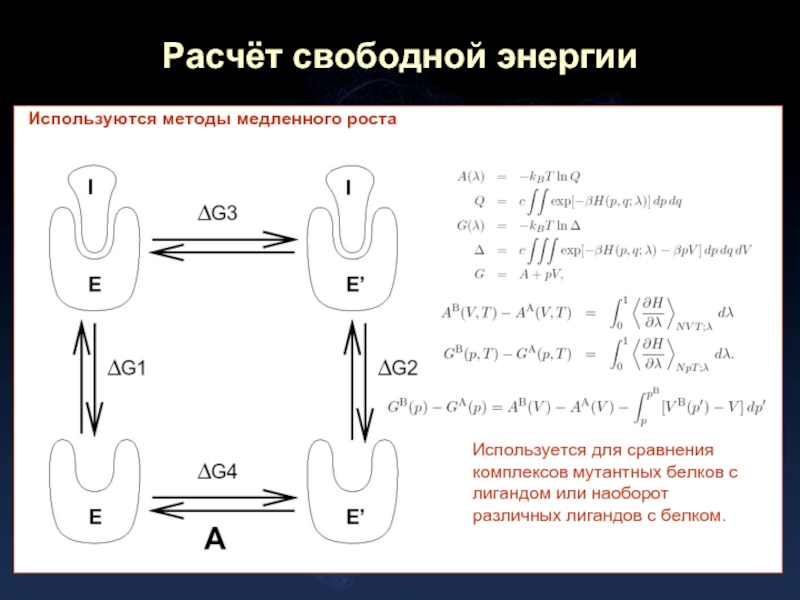
- 23. Расчёт свободной энергии Используются методы медленного
- 24. Существенная динамика (principal component analysis,essential dynamics)
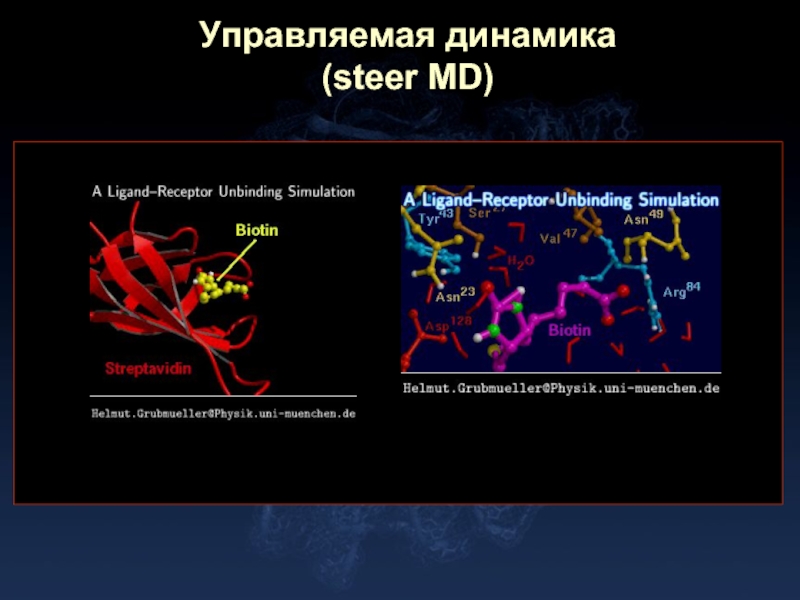
- 25. Управляемая динамика (steer MD)
- 26. Анализ траекторий Gromacs предоставляет более 50
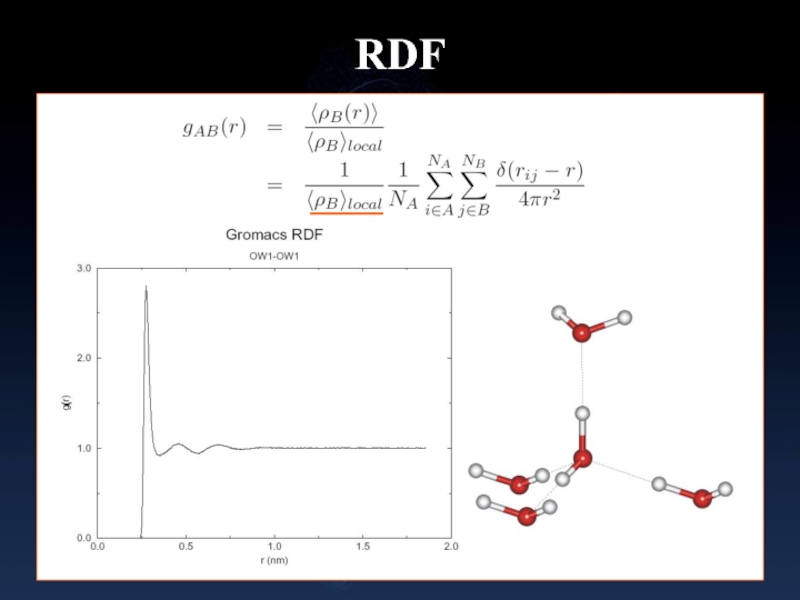
- 27. RDF
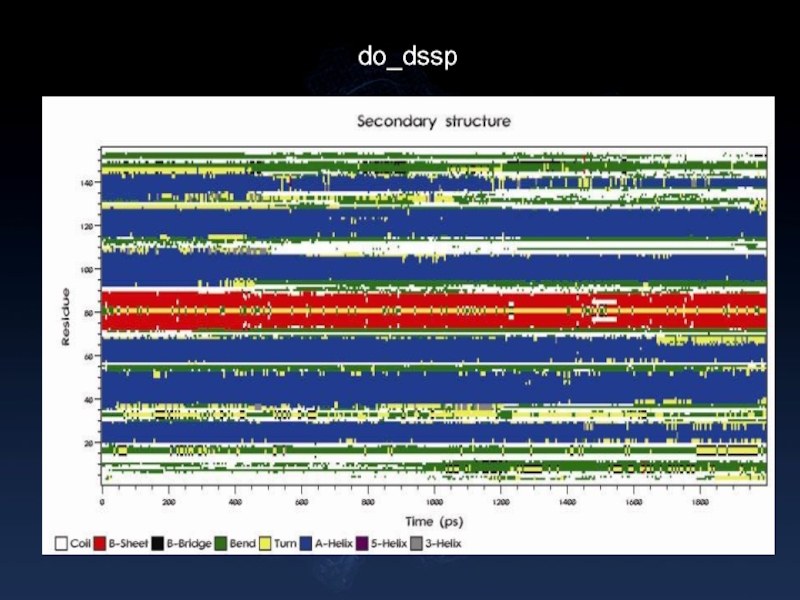
- 28. do_dssp
- 29. ………….
Слайд 2Молекулярная механика
Основы:
Симуляции подчиняются законам классической физики. Движущая сила : Функции потенциальной
Использование:
Поиск конформаций биомолекул.
Исследование флуктуации и динамики биополимеров.
Расчет, как самой свободной энергии систем, так и её изменение.
Слайд 4
Силовое поле, константы
Константы из уравнения :
1) связи , Кb, b0 ИР-спектроскопия, QM
2)
3) торсионные углы Kφ, δ ИР-спектроскопия, ЯМР, QM
4) Частичные заряды qi угадывание, термодинамика,QM
5) Параметры WdV Aij, Cij угадывание,термодинамика, QM
Большинство значений можно получить из
высокоточных расчётов QM ab initio (DFT B3LYP 6-31+G*). Полученные значения "подгоняют" под уравнения силового поля.
Слайд 6Методология подготовки системы для МД
Построение топологии молекулы на основе координат
т.е. перечисление
Выбор формы и размера ячейки
Минимизация энергии структуры в вакууме
методы: steep, CG, l-bfgs
Добавление растворителя и ионов в ячейку
"Утряска" воды и ионов вокруг не подвижной
молекулы
Слайд 7
Периодичные граничные условия
МД поли-аланина показала искусственную стабилизацию альфа спирали, при использовании
Слайд 8Что можно узнать из МД?
равновесные свойства:
Константа связывания лиганда с белком
Средняя потенциальная
Распределение жидкости вокруг различных элементов
динамические и неравновесные свойства:
Вязкость жидкости
Процесс диффузии в мембраны
Динамика фазовых изменений
Кинетику реакции
Слайд 9Ограничения МД
Симуляции основаны на законе Ньютона
Электроны не учитываются
Силовые поля это приближение
Удалённые
Граничные условия между ячейками не натуралистичны
Слайд 10Длинна траектории МД
Длинна траектории должна быть в 10 раз больше чем
Слайд 12Удаленные электростатические взаимодействия
N2
Приемлемый выход это PME, particle mesh Ewald
Слайд 14Алгоритмы минимизации энергии системы
hn максимальное смещение
Steepest descent (крутой спуск)
Если
Если то новые координаты не принимаются и
Слайд 15Алгоритмы минимизации энергии системы
Conjugate Gradient (сопряженный градиент)
Окончание минимизации определяется значением
максимальной
файле.
Рекомендуется для подготовки системы к анализу
нормальных мод. Не может использоваться при
использовании ограничений (dummies).
Слайд 16Алгоритмы минимизации энергии системы
Очень эффективный алгоритм. Рекомендуется
использовать вместе с PME.
L-bfgs
Строит
Слайд 17Увеличение шага интегратора
МД
Можно присвоить атому водорода массу 2 а.е. При
этом
2. Использовать специальные конструкции. Dummies.
Слайд 18Конструкции атомов-пустышек в
GROMACS
Атомы входящие в конструкцию
Атомы - пустышки
Время расчёта
Используя атомы
Слайд 19МД с поляризацией
(Shell MD)
Используется поляризационная модель Дика и Оверхаузера. В этой
частица представляющая степени свободы электронного облака прикреплена к
ядру «пружинкой».
const
Слайд 21Броуновская динамика
Коофицент фрикции
«Процесс шума»
Используется для изучения диффузии молекул.
Можно использовать большой
Алгоритм контроля длинны связей: только LINCS
Слайд 22Анализ нормальных мод
Выявление гармонических колебаний молекулы.
Последовательность использования программ пакета GROMACS:
Mdrun –минимизация
g_nmeig - диагонализация Гессиан матрицы
g_anaeig - анализ
Слайд 23Расчёт свободной энергии
Используются методы медленного роста
Используется для сравнения комплексов мутантных
Слайд 26
Анализ траекторий
Gromacs предоставляет более 50 программ для анализа траекторий.
Можно выделить ряд
Общие свойства: g_energy, g_com
Функция кругового распеределения: g_rdf
Связи, углы, торсионые углы : g_bond, g_angle, g_sgangle
Растояния: g_gyrate, g_sgangle, g_mindist, g_mdmat
Белки : g_hbond, do_dssp, g_rama, xrama, wheel
Граница фаз: g_order, g_density, g_potential, g_coord