- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование систем. Лекция 1 презентация
Содержание
- 1. Моделирование систем. Лекция 1
- 2. Моделирование – это совокупность методик для совершенствования
- 3. История Система GPSS была разработана сотрудником фирмы IBM Джефри
- 4. Литература 32471_gpss_world_reference GPSS_EE_Help gpss_new Девятков
- 5. Курс «Моделирование цифровых устройств и системы
- 6. Тема 3.
- 7. Модель – это
- 8. Наиболее полная теория моделирования изложена в
- 9. Общая теория моделирования Классификации
- 10. Это метод исследования, основанный на том,
- 11. Осмысление реального объекта. Эксперимент
- 12. Формализация описания поведения объектов сложных систем
- 13. Написание программы модели не будет представлять
- 14. Тема реферата Основы теории вероятностей и математической
- 15. Общность СМО и Вычислительных СИСТЕМ Анализ
- 16. Системы массового обслуживания
- 17. Организация процесса моделирования Система моделирует поведение реального
- 18. Определение транзакта Транзакт, это абстрактный объект
- 19. Описание потоков заявок Поток заявок описывается
- 20. Состав системы GPSS World Язык для описания
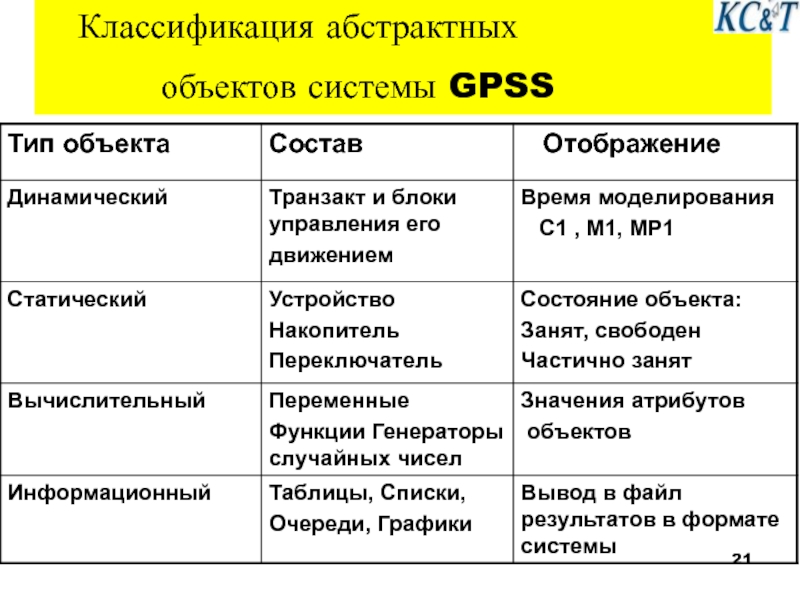
- 21. Классификация абстрактных объектов системы GPSS
- 22. Механизм создания времени генерации транзактов Механизм управления
- 23. Формирование входных воздействий в
- 24. Пояснения к решению задачи моделирования входных
- 25. Визуализация процесса моделирования Равномерный закон времён поступления
- 26. Моделирование экспоненциального распределения
- 27. GENERATE (Normal(1,150,10))
- 28. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Найти учебную
Слайд 2Моделирование – это совокупность
методик для совершенствования исследования сложных систем
Введение
В настоящее время моделирование используется
во всех направлениях деятельности человека.
Большинство систем моделирования ориентируется на конкретные области техники: emPlant – машиностроение, Delmia – судостроение, Netrac – телекоммуникация и связь, VHDL - цифровые устройства. Системы общего назначения -
GPSS World, Anylogic, Simula, ProcessModel, AutoMod.
General Purpose Simulation System
Слайд 3История
Система GPSS была разработана сотрудником фирмы IBM Джефри Гордоном в 1961 году.
Гордоном были созданы 5
GPSS III (1965), GPSS/360 (1967) и GPSS V (1971). Известный ранее только специалистам,
в нашей стране этот программный пакет завоевал популярность после издания в СССР в 1980 году
монографии Т Дж. Шрайбера.
В ней была рассмотрена одна из ранних версий языка — GPSS/360,
а также основные особенности более мощной версии — GPSS V, поддерживаемой компанией IBM,
у нас она была более известна как пакет моделирования дискретных систем (ПМДС).
Этот пакет работал в среде подсистемы диалоговой обработки системы виртуальных машин единой серии (ПДО СВМ ЕС) ЭВМ.
После окончания поддержки GPSS V компанией IBM следующей версией стала система GPSS/H компании
Wolverine Software разработанная в 1978 году под руководством Дж. Хенриксена. В 1984 году
появилась первая версия GPSS для персональных компьютеров с операционной системой DOS — GPSS/PC. Она была разработана компанией Minuteman Software под руководством С. Кокса. Конец XX века ознаменовался разработкой компанией Minuteman Software программного продукта GPSS World, увидевшей свет в 1993 году.
За сравнительно небольшой период времени было выпущено несколько его версий,
причем в каждой последующей возможности системы моделирования наращивались. Помимо этих основных версий существует также Micro-GPSS,
разработанная Ингольфом Сталлом в Швеции, — это упрощенная версия, предназначенная для изучения языка GPSS, и WebGPSS,
также предназначенная для изучения работы системы и разработки простейших имитационных моделей в сети интернет.
История
Система GPSS была разработана сотрудником фирмы IBM Джефри Гордоном в 1961 году. Гордоном были созданы 5 первых версий языка: GPSS (1961), GPSS II (1963), GPSS III (1965), GPSS/360 (1967) и GPSS V (1971). Известный ранее только специалистам, в нашей стране этот программный пакет завоевал популярность после издания в СССР в 1980 году монографии Т Дж. Шрайбера. В ней была рассмотрена одна из ранних версий языка — GPSS/360, а также основные особенности более мощной версии — GPSS V, поддерживаемой компанией IBM, у нас она была более известна как пакет моделирования дискретных систем (ПМДС). Этот пакет работал в среде подсистемы диалоговой обработки системы виртуальных машин единой серии (ПДО СВМ ЕС) ЭВМ. После окончания поддержки GPSS V компанией IBM следующей версией стала система GPSS/H компании Wolverine Software разработанная в 1978 году под руководством Дж. Хенриксена. В 1984 году появилась первая версия GPSS для персональных компьютеров с операционной системой DOS — GPSS/PC. Она была разработана компанией Minuteman Software под руководством С. Кокса. Конец XX века ознаменовался разработкой компанией Minuteman Software программного продукта GPSS World, увидевшей свет в 1993 году. За сравнительно небольшой период времени было выпущено несколько его версий, причем в каждой последующей возможности системы моделирования наращивались. Помимо этих основных версий существует также Micro-GPSS, разработанная Ингольфом Сталлом в Швеции, — это упрощенная версия, предназначенная для изучения языка GPSS, и WebGPSS, также предназначенная для изучения работы системы и разработки простейших имитационных моделей в сети интернет.
Слайд 4 Литература
32471_gpss_world_reference
GPSS_EE_Help
gpss_new
Девятков В. В. Руководство пользователя по GPSS World. Издательство
Слайд 5Курс «Моделирование цифровых устройств и
системы автоматизированного проектирования
Тема 1.
Общие
классификация. Основные уровни моделирования сложных
систем. Имитационное моделирование концептуальных и
реальных объектов. Основы формализации
сложных систем при имитационном моделировании.
Аналитическое представление сложной системы.
Характеристики реальных сложных систем. Понятие события,
процесса, активности.
Тема 2.
Имитационное моделирование вычислительных систем.
Описание поведения сложной системы для построения
имитационной модели. Принципы моделирования
параллельных процессов и одновременных событий.
Способы реализации квазипараллелизма в моделях.
Способы формализации вычислительной системы для
организации в имитационных моделях
квазипараллелизма: просмотр активностей, составление
расписания событий, транзактный, процессный, агрегатный.
Слайд 6
Тема 3.
Элементы теории массового обслуживания. Организация
случайных
Закон Пуассона и его использование для описания процессов
в системах массового обслуживания.
Описание различных функций распределения случайных
событий в системе моделирования. Аналитические
зависимости для анализа характеристик вычислительной
системы как системы массового обслуживания.
Тема 4.
Показатели работоспособности вычислительной системы:
быстродействие, загрузка ЭВМ, производительность. Основные
факторы, определяющие производительность вычислительной
системы. Одномерный и многомерный потоки заявок. Закон
сохранения времени ожидания. Характеристики различных
дисциплин обслуживания. Зависимость характеристик
вычислительной системы от ее конфигурации.
Слайд 7
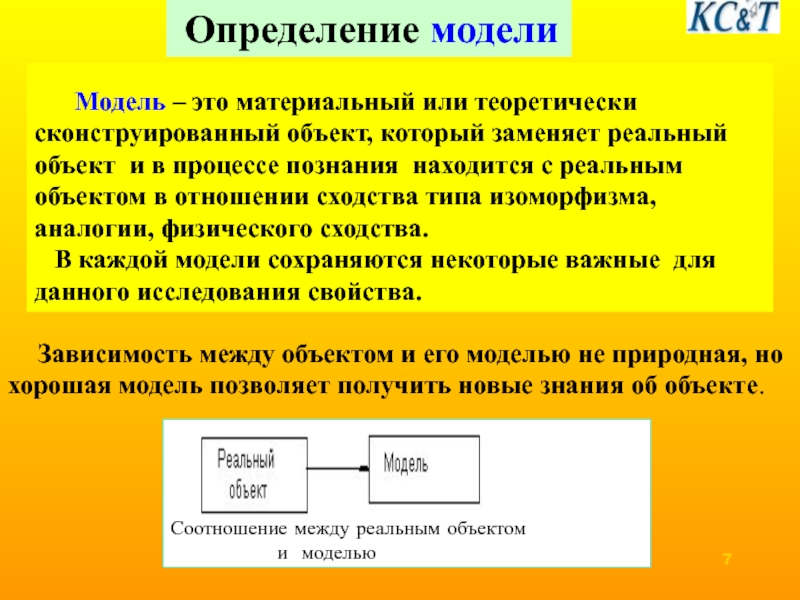
Модель – это материальный или теоретически сконструированный объект,
В каждой модели сохраняются некоторые важные для данного исследования свойства.
Зависимость между объектом и его моделью не природная, но хорошая модель позволяет получить новые знания об объекте.
Определение модели
Соотношение между реальным объектом
и моделью
Слайд 8 Наиболее полная теория моделирования изложена в книге
Р. Шеннона «Имитационное
Основные качества модели
Модель не существует изолированно от объекта, так как она строится на основе реального объекта.
2. Модель при всем своем сходстве с оригиналом по основным признакам, всегда отличается от оригинала. Чаще всего модель отражает те свойства оригинала, которые существенны для того, кто использует реальный объект.
3. Модель всегда имеет целевое назначение. Модель представляет некую систему исследований, служащую средством получения информации о реальном объекте.
Слайд 9
Общая теория моделирования
Классификации моделей
Способы реализации модели
Характер воспроизводимых
объектов
Способы получения информации о
поведении модели.
Слайд 10 Это метод исследования, основанный на том,
что изучаемая динамическая
эксперименты с целью получения информации
об изучаемой системе.
Чтобы решить задачу имитационного моделирования нужно
обеспечить взаимодействие трех видов познания:
логического, физического, семиотического.
Логическое познание – способ описания объекта – формулы, алгоритмы
Физическое познание – представление результата формализации некоторыми аналогами
Семиотическое познание - система знаков, символов для
представления и интерпретации результатов моделирования
Имитационное моделирование
Слайд 11
Осмысление реального объекта.
Эксперимент над объектом (вместо эксперимента над реальным объектом)
3. Прогнозирование характеристик и поведения системы.
4. Организация взаимодействия с устройствами обработки информации о работе системы.
5. Обучение и тренировка пользователей системы.
Определение целей имитационного
моделирования
Слайд 12Формализация описания поведения объектов сложных систем
2. Описание функционирования
реального объекта для
3. Структурная схема имитационных моделей
4. Понятие квазипараллелизма в моделях СС
5. Организация квазипараллелизма в имитационных моделях
Слайд 13 Написание программы модели не будет представлять
большой сложности, так как
компонент и их характеристик достаточно прост
и создан по правилам формирования языков
программирования.
Разработка имитационной модели
Представление результатов моделирования, их анализ и
описание рекомендаций по проектированию или
эксплуатации исследуемых Цифровых Систем требует
знания теории вероятностей и методов планирования
эксперимента, что обычно предполагается в инженерном
образовании.
Слайд 14Тема реферата
Основы теории вероятностей и математической статистики
1. Основные понятия теории вероятностей.
2.
3. Способы описания функций распределения. Основные параметры
функций распределения.
4. Формулы для вычисления параметров функций для указанных
ниже распределений:
Равномерный закон
Экспоненциальный закон
Закон Пуассона
Нормальный закон
Закон Парето
5. Области применения функций распределения каждого из названных
видов функций. Срок выполнения 3 недели.
Объём работы не более 4 страниц формата А4.
Необходимо представить графики всех названных функций
с указанием на графиках параметров функций распределения.
Материал представлять в электронном виде.
Адрес почты: irina-babalova@rambler.ru
Слайд 15Общность СМО и Вычислительных СИСТЕМ
Анализ вычислительных и информационных систем
показывает,
В ВС есть определенный набор компонент, к которым
предъявляются требования по обработке запросов.
Эти требования не всегда могут быть реализованы в связи с тем, что количество предоставляемых ресурсов ограничено.
Наиболее трудоемкими этапами моделирования являются
шаги по представлению вычислительных систем в формате компонент СМО, определению и описанию характеристик этих компонент. Надо суметь четко сформулировать требования к системе и знать законы ее функционирования.
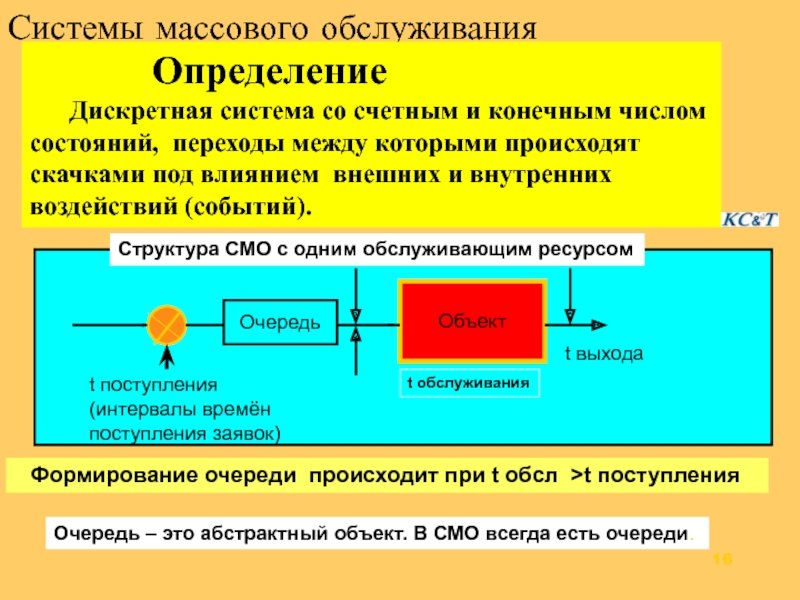
Слайд 16Системы массового обслуживания
Определение
Очередь
Объект
t поступления
(интервалы времён поступления заявок)
t обслуживания
t выхода
Формирование очереди происходит при t обсл >t поступления
Очередь – это абстрактный объект. В СМО всегда есть очереди.
Структура СМО с одним обслуживающим ресурсом
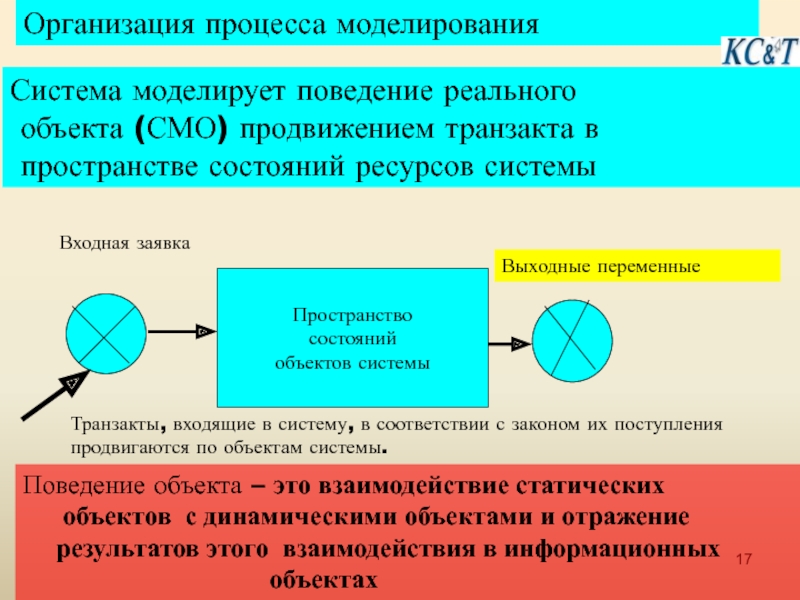
Слайд 17Организация процесса моделирования
Система моделирует поведение реального
объекта (СМО) продвижением транзакта
пространстве состояний ресурсов системы
Пространство
состояний
объектов системы
Входная заявка
Выходные переменные
Транзакты, входящие в систему, в соответствии с законом их поступления продвигаются по объектам системы.
Поведение объекта – это взаимодействие статических
объектов с динамическими объектами и отражение
результатов этого взаимодействия в информационных
объектах
Слайд 18Определение транзакта
Транзакт, это абстрактный объект
модели, связанный с входными воздействиями
на
Время существования Транзакта -
это время моделирования всего объекта
или время в той части модели,
в которой этот транзакт двигался.
Каждый транзакт имеет свои атрибуты и
параметры, не связанные со временем.
Все транзакты модели имеют свой порядковый
номер.
Основные блоки, работающие с транзактами:
Generate, Terminate, Priority, Mark, Assign, Gate, Test, Transfer, Advance, Split, Assembly, Gather,
Matсh
Слайд 19Описание потоков заявок
Поток заявок описывается моментами времени поступления заявок в
Законы поступления заявок могут быть детерминированными или случайными
Элементы теории вероятностей
Характеристики законов распределения случайных значений
Простейший поток и его свойства
Генерация случайных величин по закону Пуассона
Вычисление значений функций распределения
через равномерно распределенные случайные числа на
заданном интервале времен. Теорема.
Слайд 20Состав системы GPSS World
Язык для описания моделей и
командный язык для связи
моделирующей программы
2. Транслятор, состоящий из синтаксического
анализатора интерпретирующего типа и
препроцессора, формирующего результаты
моделирования
3. Монитор – управляющая программа,
выполняющая построчный анализ программы –
модели и исполнение каждой строки программы
Слайд 22Механизм создания времени генерации транзактов
Механизм управления количеством запусков модели
Атрибуты транзактов
Блоки
Визуализация процесса моделирования
Создание программы модели
Запуск программы модели
ОКНО результатов
Файл результатов (вывод таблиц)
Основные блоки, работающие с транзактами:
Generate, Terminate, Priority, Mark, Assign, Gate, Test, Transfer, Advance, Split, Assembly, Gather,
Matсh
Лабораторная работа № 1
Слайд 23Формирование входных воздействий
в системе GPSS World
Случайные
времен появления заявок
Система позволяет использовать множество генераторов случайных чисел RN1, RN2,…. RN100…. Система моделирования автоматически настраивается на заданный диапазон входных воздействий. [ A, B ]
Наиболее известные функции распределения случайных чисел - это нормальное и пуассоновское, экспоненциальное,равномерное..
GENERATE 150,50
GENERATE (Exponential(1,0,150))
GENERATE (Poisson(2,150))
GENERATE (Normal(1,150,50)) =10
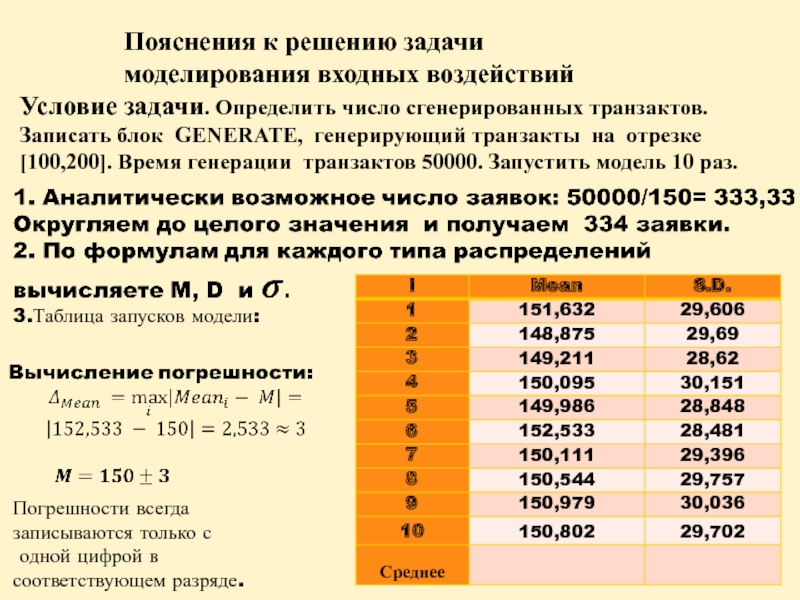
Слайд 24Пояснения к решению задачи
моделирования входных воздействий
Условие задачи. Определить число сгенерированных
3.Таблица запусков модели:
Погрешности всегда
записываются только с
одной цифрой в
соответствующем разряде.
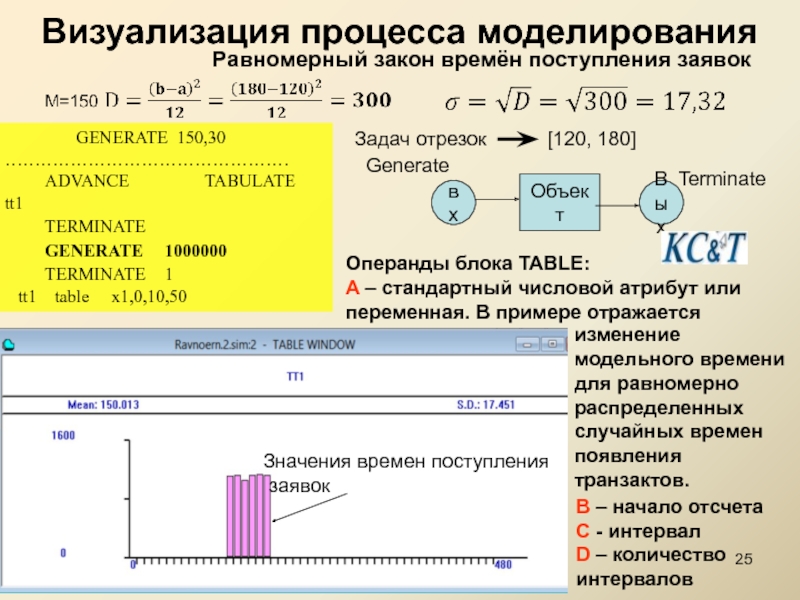
Слайд 25Визуализация процесса моделирования
Равномерный закон времён поступления заявок
…………………………………………
ADVANCE TABULATE tt1
TERMINATE
GENERATE 1000000
TERMINATE 1
tt1 table x1,0,10,50
вх
Объект
Вых
Операнды блока TABLE:
A – стандартный числовой атрибут или переменная. В примере отражается
изменение
модельного времени
для равномерно
распределенных
случайных времен
появления транзактов.
B – начало отсчета
C - интервал
D – количество
интервалов
Значения времен поступления
заявок
Задач отрезок [120, 180]
Generate
Terminate
Слайд 26
Моделирование экспоненциального распределения
В описании функции распределения времен поступления заявок значения параметров:
1- номер генератора
случайных чисел
S – сдвиг
распределения
σ =среднее квадратичное отклонение
Все параметры –
положительные
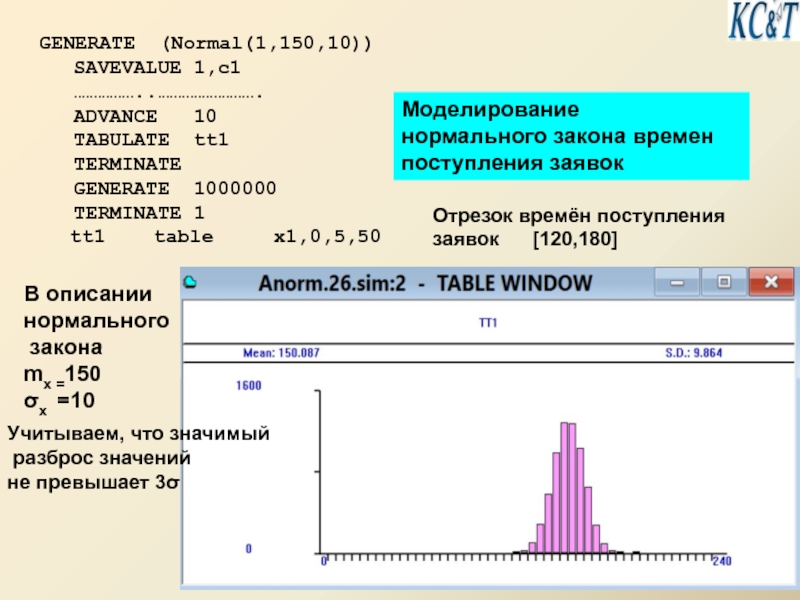
Слайд 27 GENERATE (Normal(1,150,10))
SAVEVALUE 1,c1
……………..…………………….
ADVANCE 10
TABULATE tt1
TERMINATE
GENERATE 1000000
TERMINATE 1
tt1
Моделирование
нормального закона времен
поступления заявок
В описании
нормального
закона
mx =150
σx =10
Отрезок времён поступления заявок [120,180]
Учитываем, что значимый
разброс значений
не превышает 3σ
Слайд 28ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Найти учебную литературу по моделированию
Установить на своих компьютерах
имитационного моделирования GPSS World (GPSSW)
3. Найти каталог примеров и просмотреть самые простые
примеры.
Адрес последней версии системы для университетов:
http://primat.org/load/poleznyj_soft/modelirovanie/
gpss_world_besplatnaja_studencheskaja_versija/28-1-0-117
Адрес почты для присылки ваших работ:
irina-babalova@rambler.ru