- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множественное выравнивание презентация
Содержание
- 1. Множественное выравнивание
- 2. Множественное выравнивание … это то же, что парное, только последовательностей сколько угодно ☺
- 3. Для чего строят множественные выравнивания?
- 4. Множественное выравнивание гомеодоменов Красным выделены консервативные
- 5. Биологический смысл Тот же, что у парного:
- 6. Парное и множественное выравнивание
- 7. (С) А.Б.Рахманинова Змей-Горыныч биоинформатики Биологическая
- 8. Парное выравнивание: вес >P1 ALGTEEIC >P2 ALGTIAA
- 9. Множественное выравнивание: формализация и алгоритмизация Можно определить
- 10. «Эвристический алгоритм (эвристика) — алгоритм решения задачи,
- 11. Руководящее дерево Очевидный недостаток:«один раз гэп
- 12. Программы множественного выравнивания ClustalW – к
- 13. Форматы хранения выравниваний Fasta Aln (он же
- 14. Редакторы выравниваний GeneDoc (установлен у нас) BioEdit
Слайд 2Множественное выравнивание
… это то же, что парное, только последовательностей сколько угодно
Слайд 3
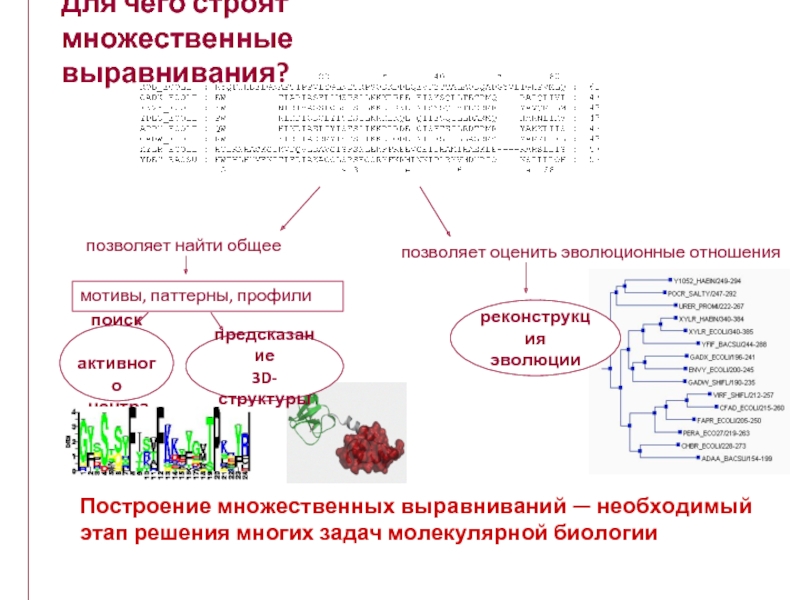
Для чего строят множественные выравнивания?
позволяет оценить эволюционные отношения
Построение множественных выравниваний
поиск
активного
центра
Слайд 4Множественное выравнивание гомеодоменов
Красным выделены консервативные (одинаковые у всех) остатки;
желтым – на
Красным выделены консервативные и функционально консервативные остатки
Слайд 5Биологический смысл
Тот же, что у парного: сопоставляемые остатки разных белков должны:
выполнять аналогичную функцию;
одинаково располагаться в пространстве.
Множественное выравнивание последовательностей использует больше информации, чем парное, поэтому (теоретически) должно в среднем чаще получаться биологически осмысленным.
Слайд 6
Парное и множественное выравнивание
Любое множественное выравнивание порождает набор
2. Не любой набор парных выравниваний можно просто
"сложить" во множественное выравнивание.
Пример:
P1 ALGTEEIC-
P2 ALGT--IAA
+ P1 AL-GTEEI-C
P1 AL-GTEEI-C P2 AL-GT--IAA
P3 ALVGTE-IAC P3 ALVGTE-IAC
+
P2 AL-GT-IAA
P3 ALVGTEIAC
≠
Слайд 7
(С) А.Б.Рахманинова
Змей-Горыныч биоинформатики
Биологическая задача −
поставить друг под другом
гомологичные позиции
Математическая
найти способ количественного
сравнения качества
выравниваний.
Программирование − создание
эффективного алгоритма и
его реализация
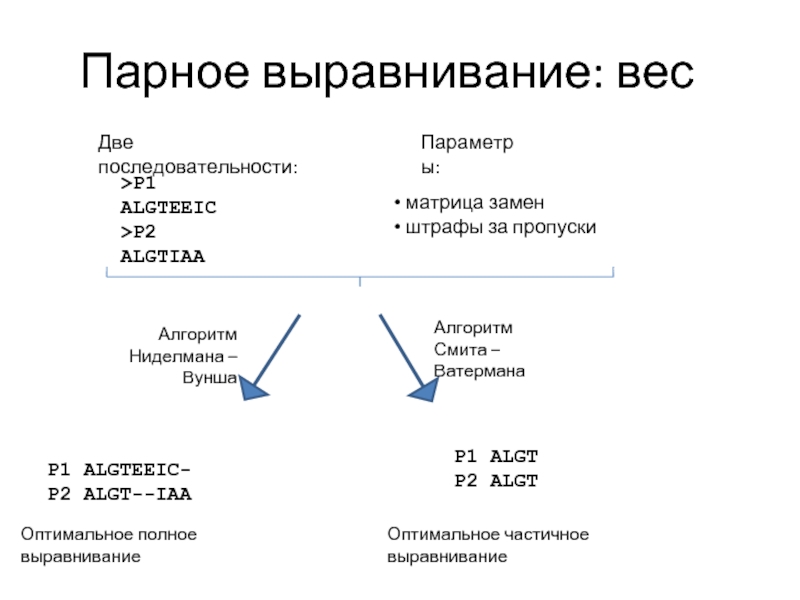
Слайд 8Парное выравнивание: вес
>P1
ALGTEEIC
>P2
ALGTIAA
Две последовательности:
Параметры:
матрица замен
штрафы
Алгоритм
Ниделмана – Вунша
Алгоритм
Смита – Ватермана
P1 ALGTEEIC-
P2 ALGT--IAA
P1 ALGT
P2 ALGT
Оптимальное полное выравнивание
Оптимальное частичное выравнивание
Слайд 9Множественное выравнивание: формализация и алгоритмизация
Можно определить вес (хотя ситуация со штрафами
Но ни для какого определения веса не существует приемлемого (по времени работы) алгоритма, который гарантировал бы нахождение оптимального по весу выравнивания.
Аналог алгоритма Ниделмана – Вунша имеет приемлемое время работы лишь для очень малого числа последовательностей (до 4–5)
Слайд 10«Эвристический алгоритм (эвристика) — алгоритм решения задачи, не имеющий строгого обоснования,
В задаче множественного выравнивания приходится использовать эвристические алгоритмы
Слайд 11
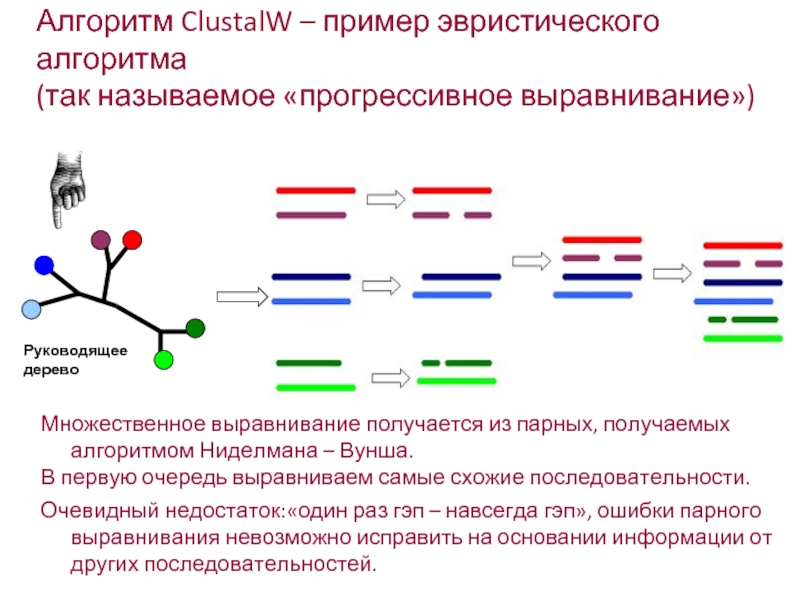
Руководящее дерево
Очевидный недостаток:«один раз гэп – навсегда гэп», ошибки парного выравнивания
Алгоритм ClustalW – пример эвристического алгоритма
(так называемое «прогрессивное выравнивание»)
Множественное выравнивание получается из парных, получаемых алгоритмом Ниделмана – Вунша.
В первую очередь выравниваем самые схожие последовательности.
Слайд 12Программы множественного выравнивания
ClustalW – к настоящему времени явно устарела, но
Muscle – пожалуй, на текущий момент программа первого выбора
MAFFT – тоже очень популярная программа
DiAlign
T-Coffee
Kalign
ProbCons
…
Всё это программы полного выравнивания
Единственная популярная программа частичного множественного выравнивания – MEME (ищет блоки, то есть выравнивания без пропусков)
Слайд 13Форматы хранения выравниваний
Fasta
Aln (он же Clustal)
MSF (Multiple sequence format)
PHYLIP
NEXUS
…
См. http://emboss.sourceforge.net/docs/themes/SequenceFormats.html#mult
Всё это
Слайд 14Редакторы выравниваний
GeneDoc (установлен у нас)
BioEdit (тоже установлен)
Mega (тоже установлена)
JalView
ClustalX
…
См. http://en.wikipedia.org/wiki/List_of_alignment_visualization_software
