- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МНОГОГРАННЫЕ УГЛЫ презентация
Содержание
- 1. МНОГОГРАННЫЕ УГЛЫ
- 2. Вертикальные многогранные углы На рисунках приведены примеры трехгранных, четырехгранных и пятигранных вертикальных углов
- 3. Измерение многогранных углов Рассмотрим вопрос об измерении
- 4. Трехгранные углы Выведем формулу, выражающую величину трехгранного
- 5. Многогранные углы Пусть SA1…An – выпуклый n-гранный
- 6. Трехгранные углы тетраэдра Для двугранных углов
- 7. Четырехгранные углы октаэдра Для двугранных углов
- 8. Пятигранные углы икосаэдра Для двугранных углов
- 9. Трехгранные углы додекаэдра Для двугранных углов
- 10. Трехгранные и четырехгранные углы ромбододекаэдра Задача. Найдите
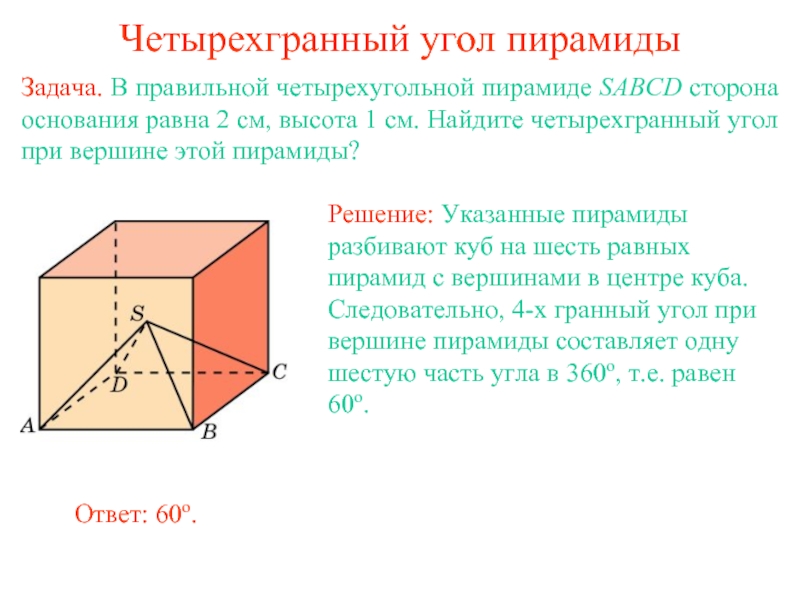
- 11. Четырехгранный угол пирамиды Задача. В правильной четырехугольной
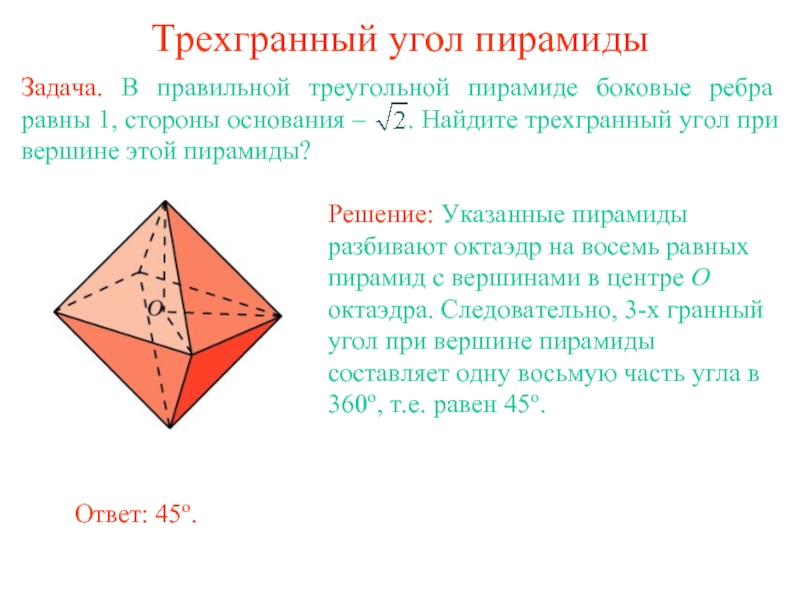
- 12. Трехгранный угол пирамиды Задача. В правильной треугольной
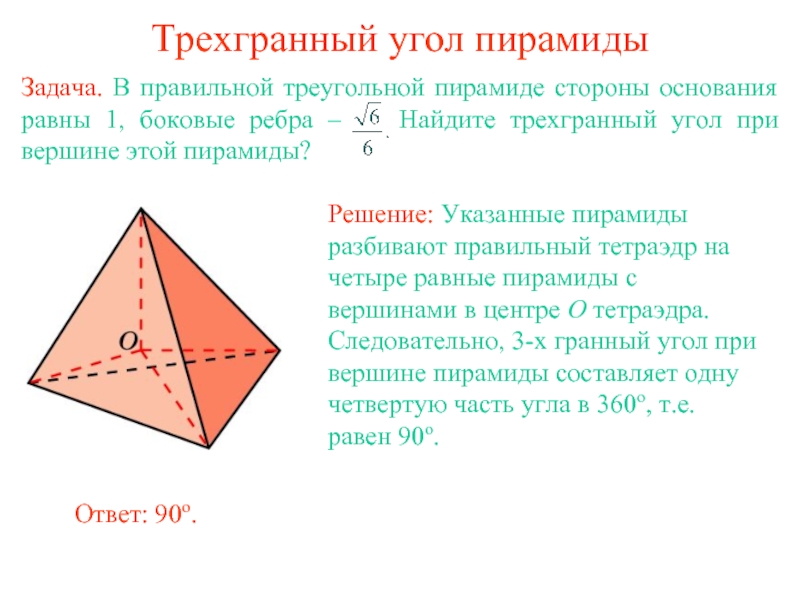
- 13. Трехгранный угол пирамиды Задача. В правильной треугольной
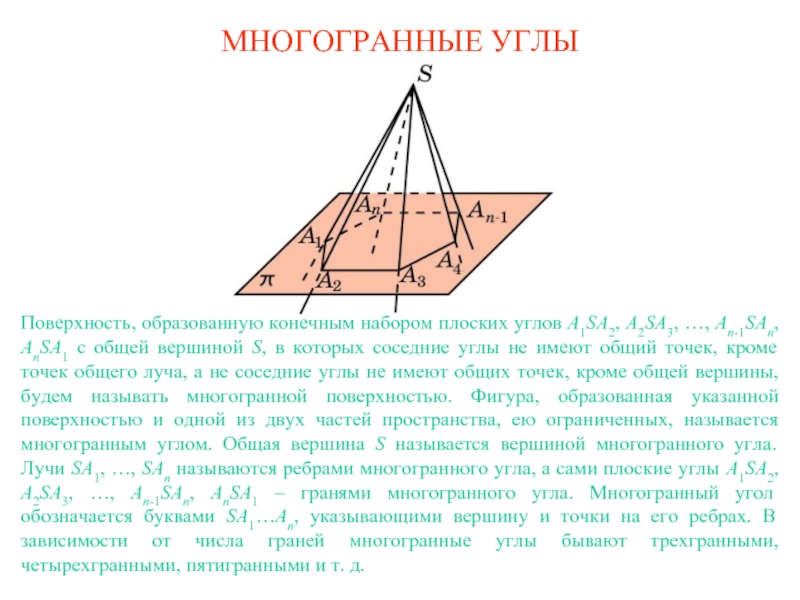
Слайд 1МНОГОГРАННЫЕ УГЛЫ
Поверхность, образованную конечным набором плоских углов A1SA2, A2SA3, …, An-1SAn,
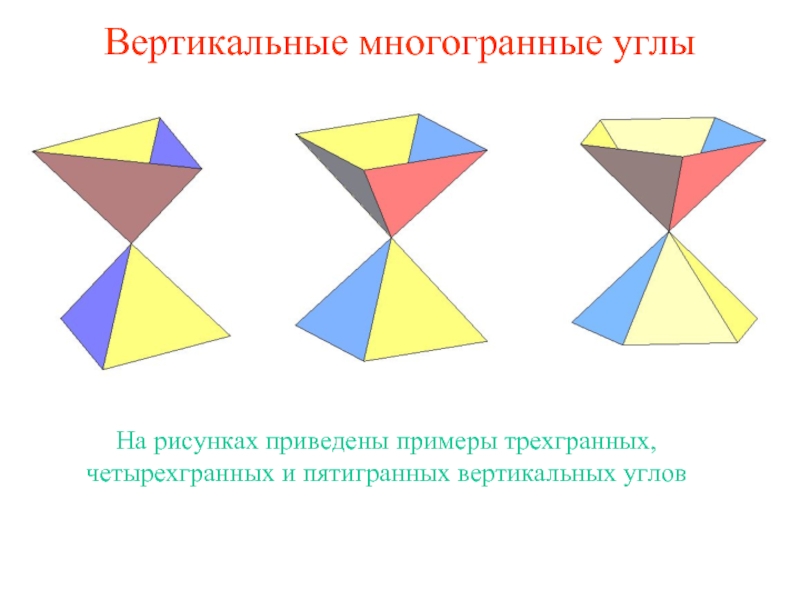
Слайд 2Вертикальные многогранные углы
На рисунках приведены примеры трехгранных, четырехгранных и пятигранных вертикальных
Слайд 3Измерение многогранных углов
Рассмотрим вопрос об измерении многогранных углов. Поскольку градусная величина
, получаем, что трехгранный угол призмы равен .
Слайд 4Трехгранные углы
Выведем формулу, выражающую величину трехгранного угла через его двугранные углы.
Плоскости граней трехгранного угла разбивают эту сферу на шесть попарно равных сферических двуугольников, соответствующих двугранным углам данного трехгранного угла. Сферический треугольник ABC и симметричный ему сферический треугольник A'B'C' являются пересечением трех двуугольников. Поэтому удвоенная сумма двугранных углов равна 360о плюс учетверенная величина трехгранного угла, или
SA + SB + SC = 180о + 2 SABC.
Таким образом, имеем следующую формулу
Слайд 5Многогранные углы
Пусть SA1…An – выпуклый n-гранный угол. Разбивая его на трехгранные
Многогранные углы можно измерять и числами. Действительно, тремстам шестидесяти градусам всего пространства соответствует число 2 , равное половине площади единичной сферы. Поэтому численной величиной многогранного угла считают половину площади сферического многоугольника, высекаемого многогранным углом из единичной сферы с центром в вершине данного многогранного угла. Переходя от градусов к числам в полученной формуле, будем иметь:
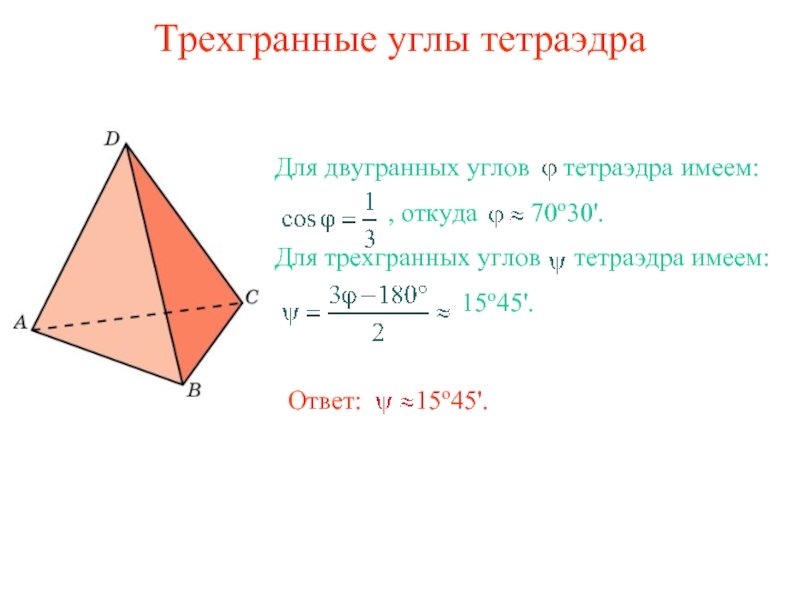
Слайд 6Трехгранные углы тетраэдра
Для двугранных углов тетраэдра имеем:
Для трехгранных углов тетраэдра имеем:
15о45'.
Ответ: 15о45'.
Слайд 7Четырехгранные углы октаэдра
Для двугранных углов октаэдра имеем:
Для четырехгранных углов октаэдра имеем:
38о56'.
Ответ: 38о56'.
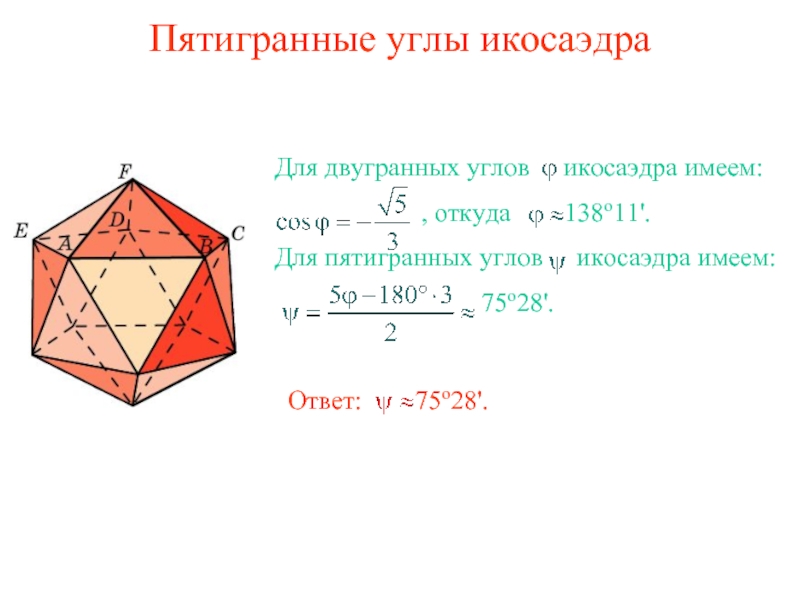
Слайд 8Пятигранные углы икосаэдра
Для двугранных углов икосаэдра имеем:
Для пятигранных углов икосаэдра имеем:
75о28'.
Ответ: 75о28'.
Слайд 9Трехгранные углы додекаэдра
Для двугранных углов додекаэдра имеем:
Для трехгранных углов додекаэдра имеем:
84о51'.
Ответ: 84о51'.