- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники и их виды. презентация
Содержание
- 1. Многогранники и их виды.
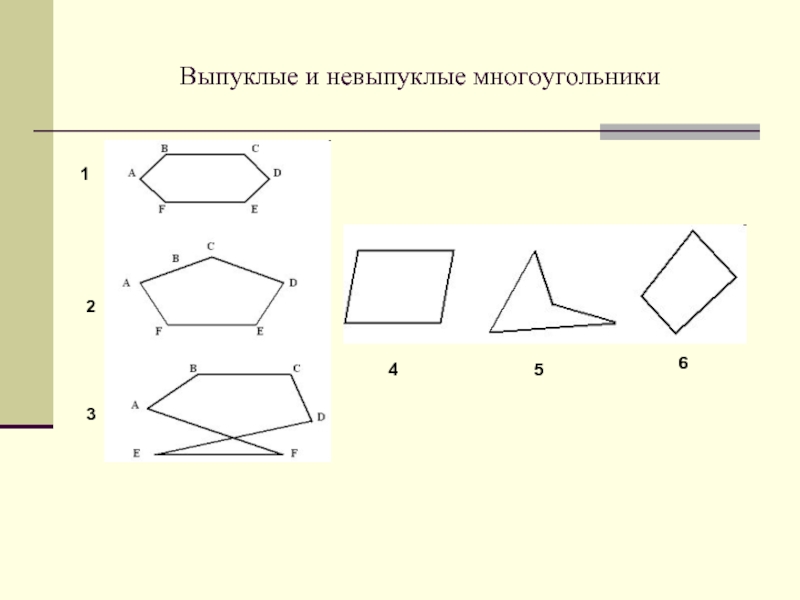
- 2. Выпуклые и невыпуклые многоугольники 1 2 3 4 5 6
- 3. Многогранником называется ограниченное тело, поверхность которого
- 4. Виды многогранников: Выпуклые и невыпуклые многогранники.
- 5. Выпуклые и невыпуклые многогранники Многогранник называется
- 6. Правильные многогранники (Платоновы тела)
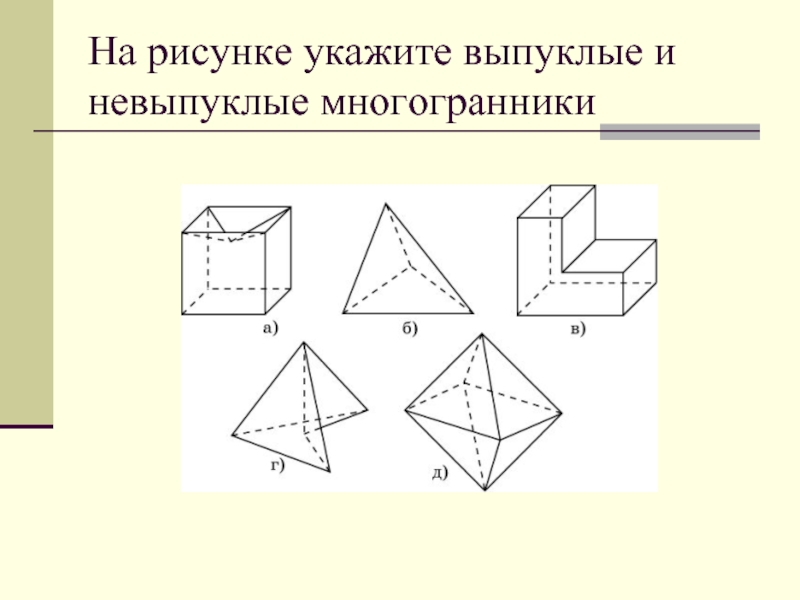
- 7. На рисунке укажите выпуклые и невыпуклые многогранники
- 8. «Правильных многогранников вызывающе мало, но этот весьма
- 9. огонь огонь вода воздух
- 10. Полуправильные многогранники Полуправильным многогранником называется выпуклый многогранник,
- 11. усеченный тетраэдр усеченный октаэдр усеченный
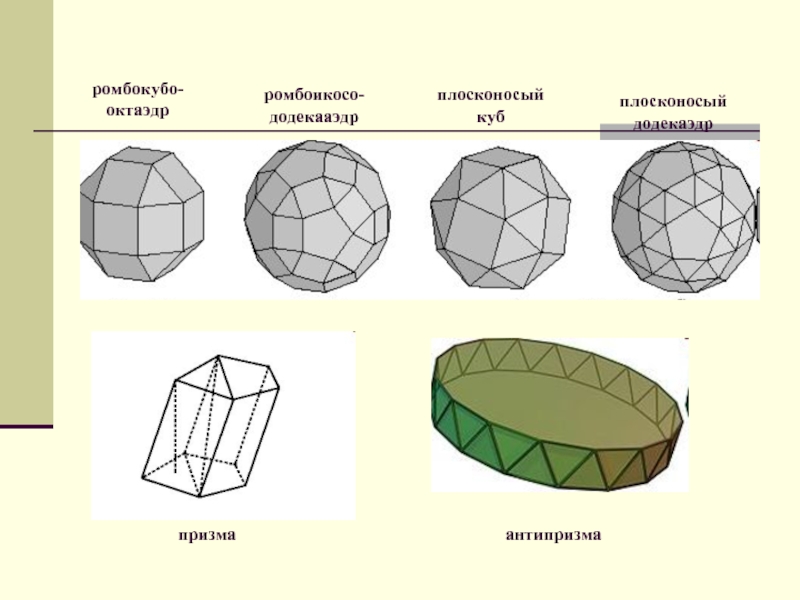
- 12. ромбокубо-октаэдр ромбоикосо-додекааэдр плосконосый куб плосконосый додекаэдр призма антипризма
- 13. Архимед (Archimedes) – ок. 287 - 212 до н.э.
- 14. Звездчатые многогранники 4 типа правильных звездчатых многогранников:
- 15. Многогранники вокруг нас
- 17. Кристаллы
- 18. Многогранники в искусстве
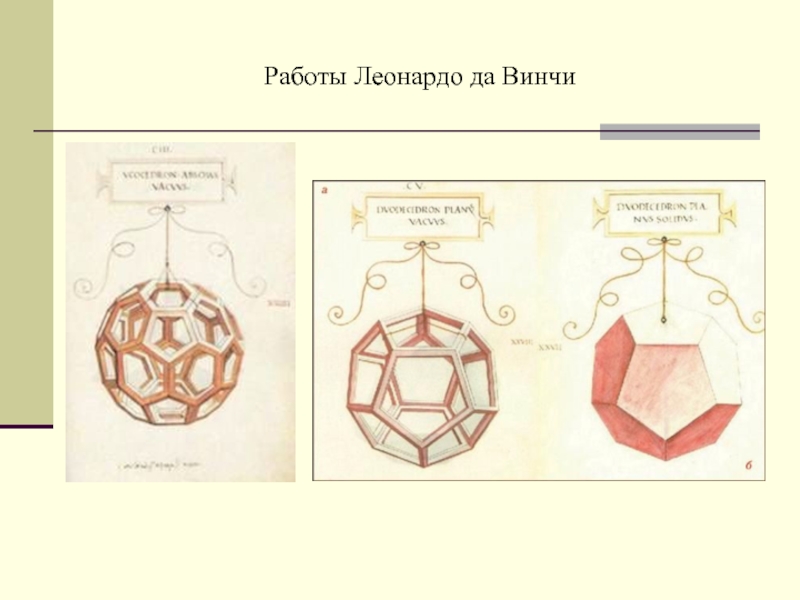
- 19. Работы Леонардо да Винчи
- 20. Многогранники в архитектуре
- 21. Пирамида Пирамидой называется многогранник, одна грань
- 22. Пирамида называется правильной,
- 23. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины.
- 24. Решение задач № 26. Основание пирамиды –
- 25. № 28. Высота и сторона четырехугольной
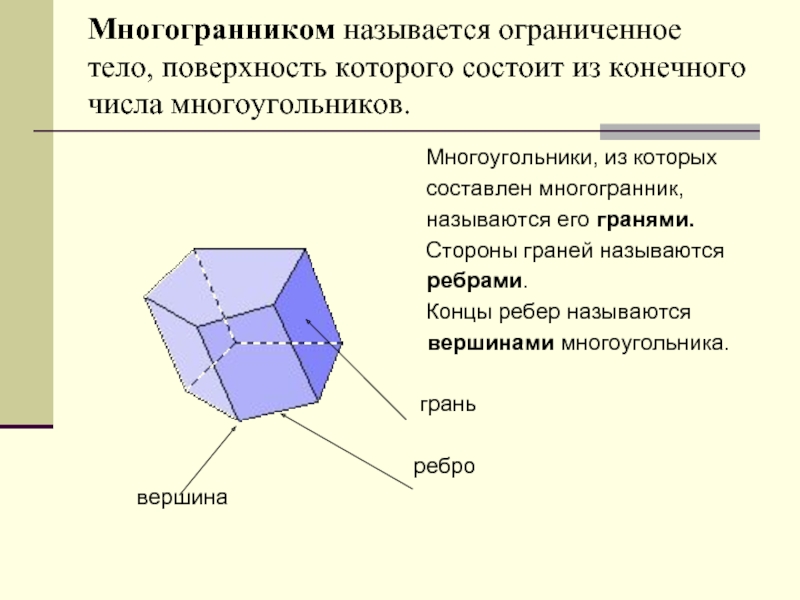
Слайд 3 Многогранником называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников.
Многоугольники, из которых
составлен многогранник,
называются его гранями.
Стороны граней называются
ребрами.
Концы ребер называются
вершинами многоугольника.
грань
ребро
вершина
Слайд 4Виды многогранников:
Выпуклые и невыпуклые многогранники.
Правильные(Платоновы тела) и неправильные многогранники.
Полуправильные многогранники.
Звездчатые
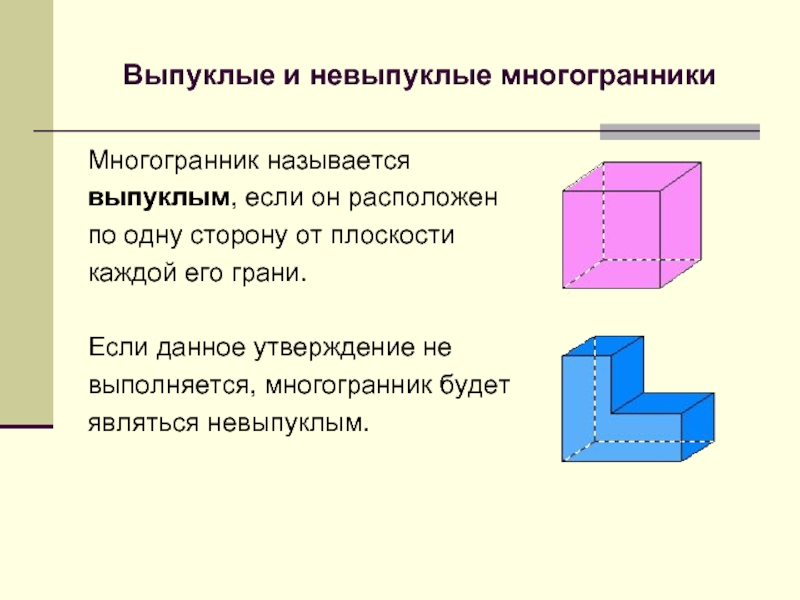
Слайд 5Выпуклые и невыпуклые многогранники
Многогранник называется
выпуклым, если он расположен
по одну
каждой его грани.
Если данное утверждение не
выполняется, многогранник будет
являться невыпуклым.
Слайд 6Правильные многогранники (Платоновы тела)
Многогранник называется правильным, если: он
По-другому правильные многогранники называются Платоновы тела.
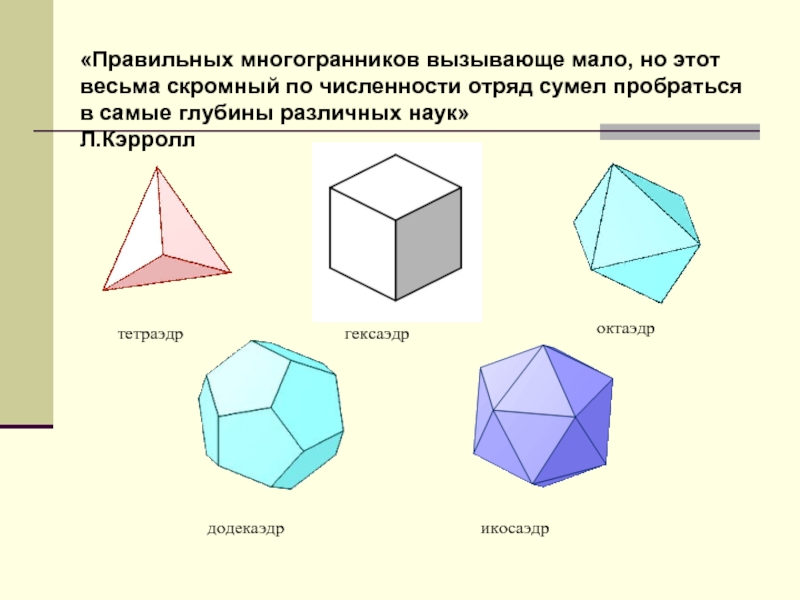
Слайд 8«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд
тетраэдр
гексаэдр
октаэдр
додекаэдр
икосаэдр
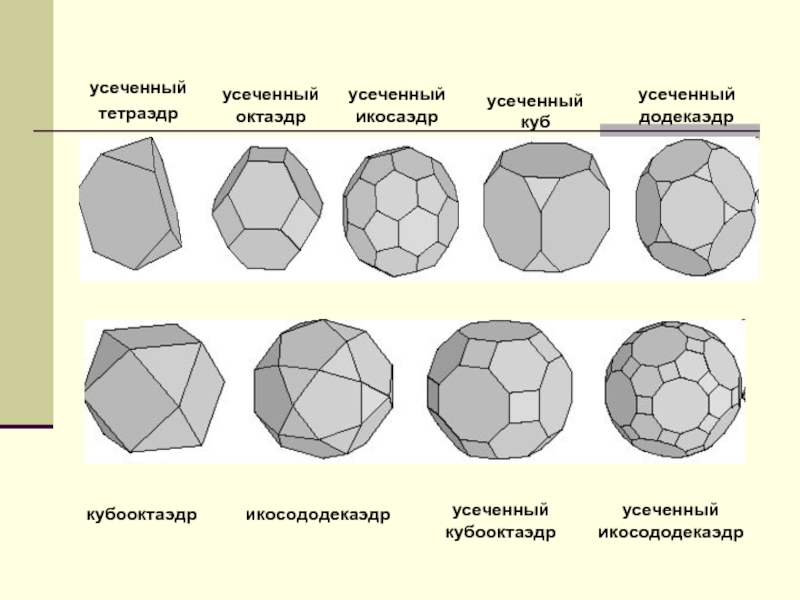
Слайд 10Полуправильные многогранники
Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники
Рассмотрим 13 полуправильных многогранников:
Слайд 11усеченный
тетраэдр
усеченный
октаэдр
усеченный
икосаэдр
усеченный
куб
усеченный
додекаэдр
кубооктаэдр
икосододекаэдр
усеченный
кубооктаэдр
усеченный
икосододекаэдр
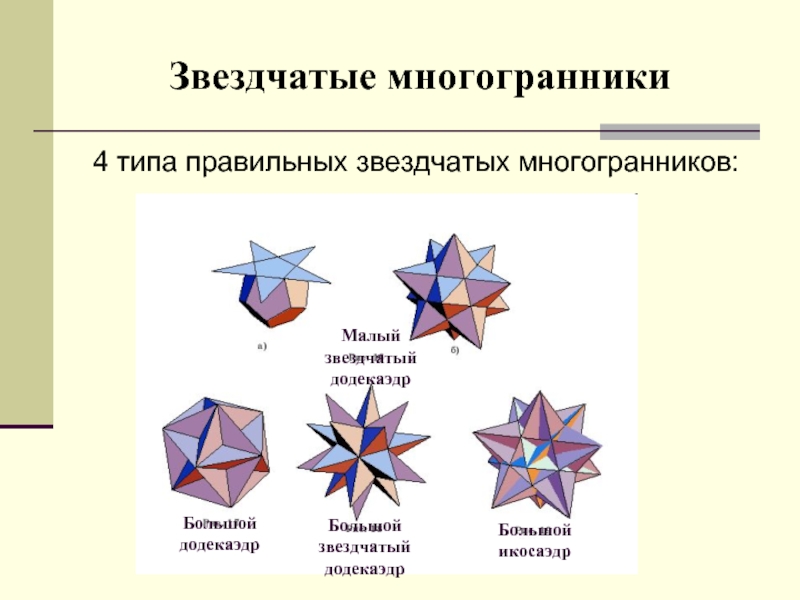
Слайд 14Звездчатые многогранники
4 типа правильных звездчатых многогранников:
Малый звездчатый додекаэдр
Большой додекаэдр
Большой звездчатый додекаэдр
Большой
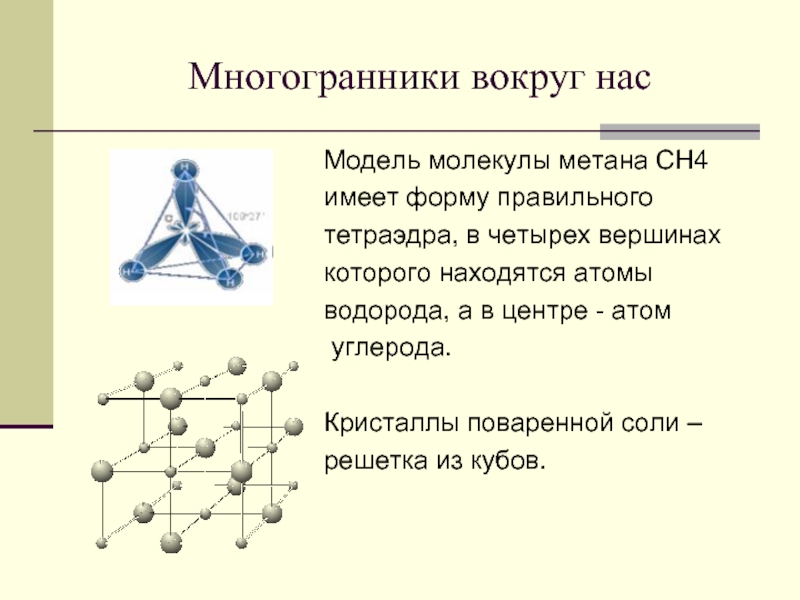
Слайд 15Многогранники вокруг нас
имеет форму правильного
тетраэдра, в четырех вершинах
которого находятся атомы
водорода, а в центре - атом
углерода.
Кристаллы поваренной соли –
решетка из кубов.
Слайд 16
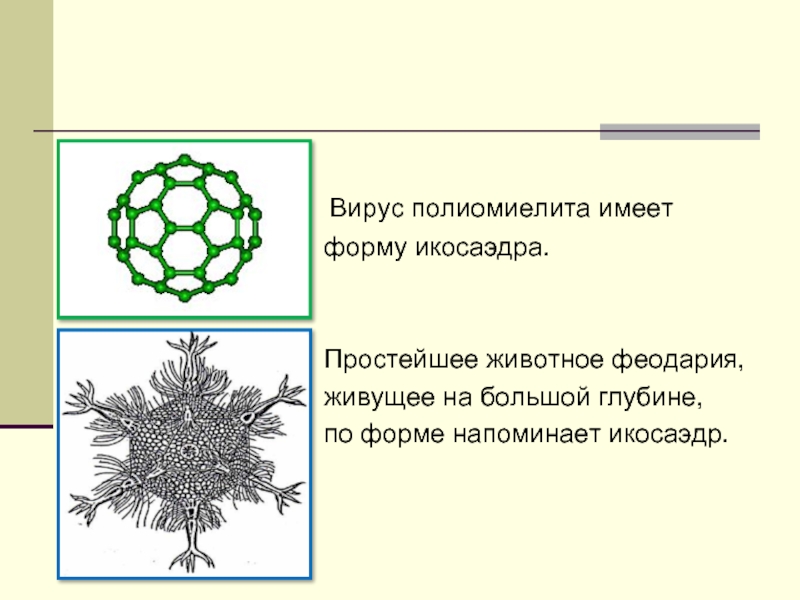
Вирус полиомиелита имеет
форму икосаэдра.
Простейшее животное феодария,
живущее на большой глубине,
по форме напоминает икосаэдр.
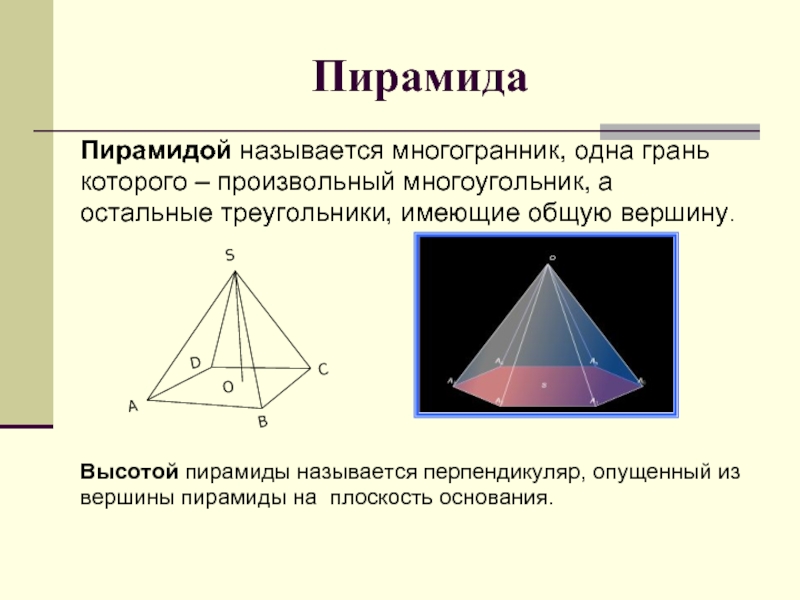
Слайд 21Пирамида
Пирамидой называется многогранник, одна грань
которого – произвольный многоугольник, а
остальные
Высотой пирамиды называется перпендикуляр, опущенный из
вершины пирамиды на плоскость основания.
Слайд 22
Пирамида называется правильной, если ее основание – правильный
В противном случае пирамида называется неправильной.
Слайд 24Решение задач
№ 26.
Основание пирамиды – прямоугольник со сторонами
6 см и
13 см. Вычислите длину высоты пирамиды.
№ 27.
Основанием пирамиды является ромб, сторона
которого равна 5 см, а одна из диагоналей – 8 см.
Найдите боковые ребра пирамиды, если высота ее
проходит через точку пересечения диагоналей
основания и равна 7 см.
Слайд 25
№ 28.
Высота и сторона четырехугольной пирамиды
соответственно равны 24 и 12
пирамиды.