- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники презентация
Содержание
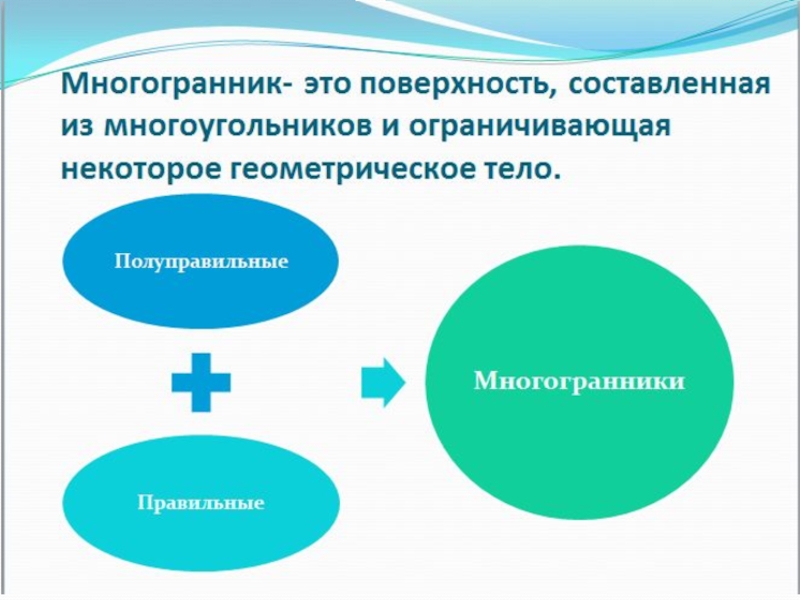
- 1. Многогранники
- 3. Правильный многогранник или платоновое тело —
- 4. Платоновыми телами называются правильные однородные выпуклые многогранники,
- 5. Почему правильные многогранники получили
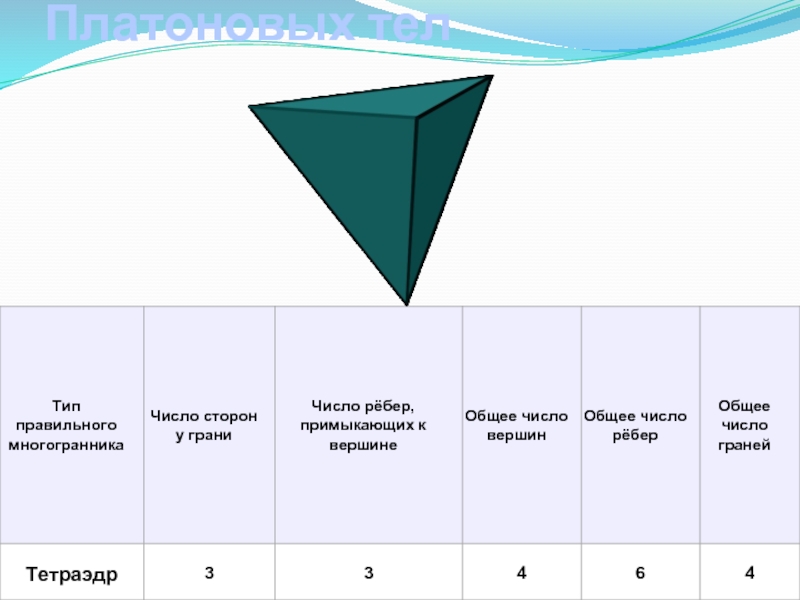
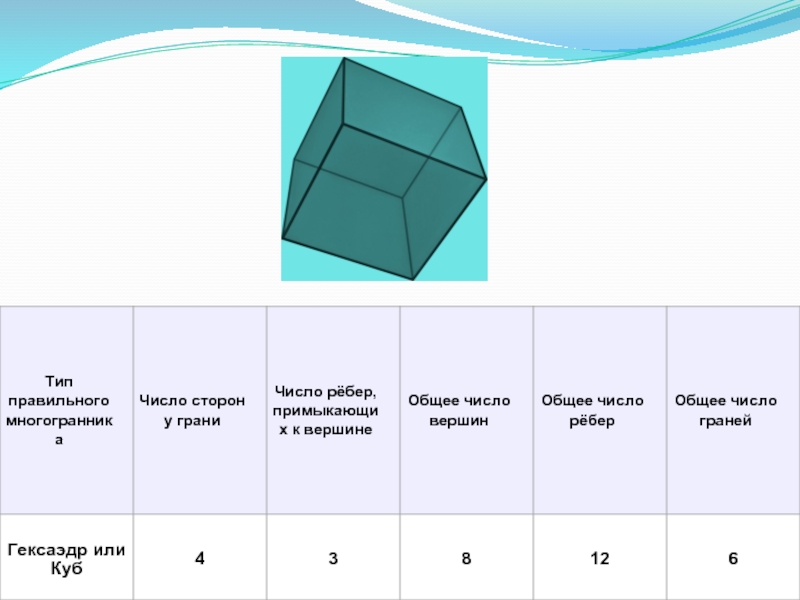
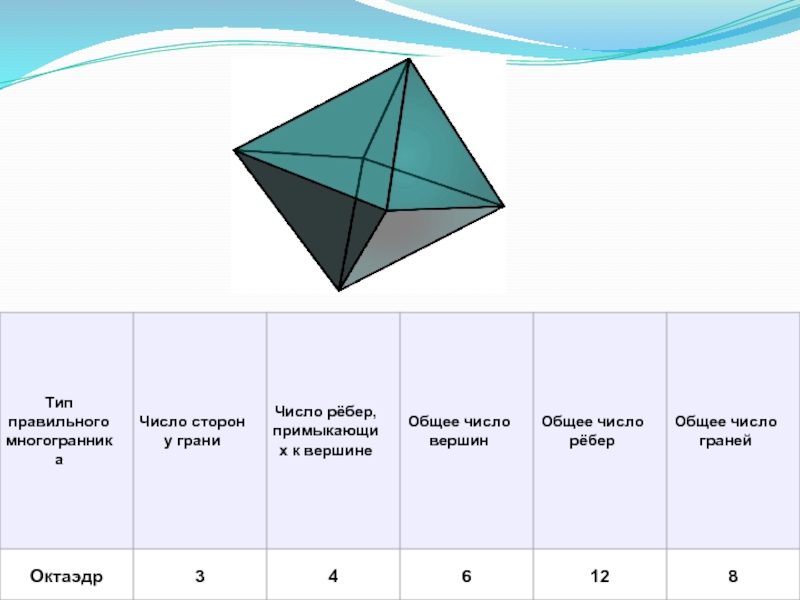
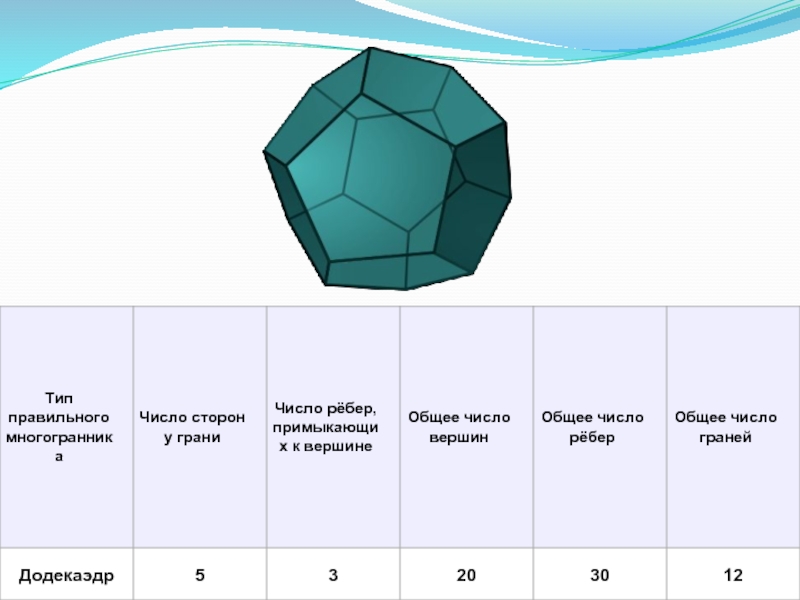
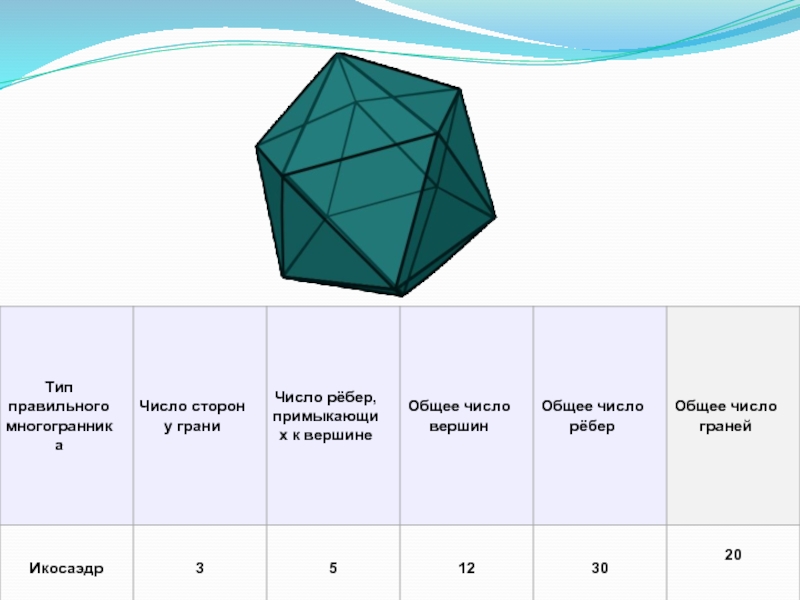
- 6. Характеристика Платоновых тел
- 11. Полуправильные многогранники - определение может варьироваться и включать
- 12. Множество Архимедовых тел можно разбить на пять
- 13. УСЕЧЕННЫЙ ИКОСАЭДР
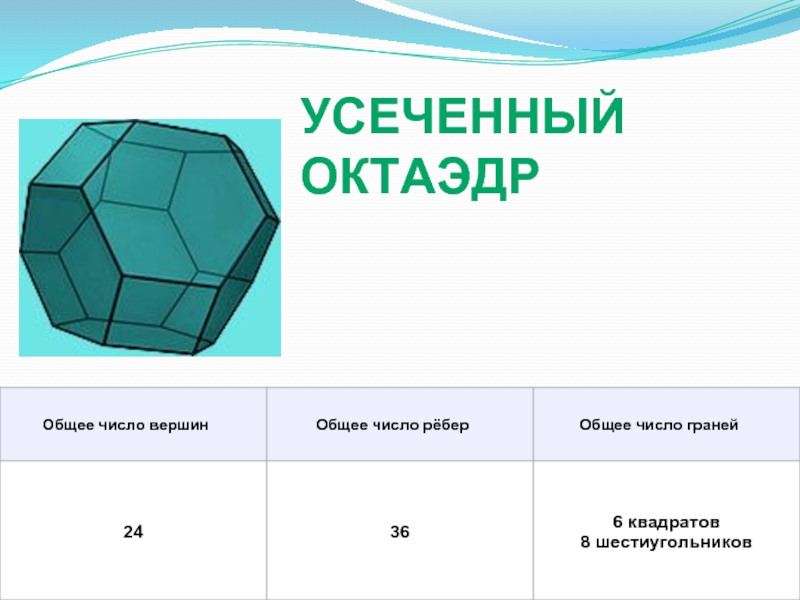
- 14. УСЕЧЕННЫЙ ОКТАЭДР
- 15. УСЕЧЕННЫЙ ТЕТРАЭДР
- 16. УСЕЧЕННЫЙ ДОДЕКАЭДР
- 17. Вторую группу Архимедовых тел составляют два тела, именуемых квазиправильными многогранниками. КУБООКТАЭДР
- 18. ИКОСОДОДЕКАЭДР
- 19. Третья группа Архимедовых тел, в нее входят: РОМБОКУБООКТАЭДР
- 20. РОМБОИКОСОДОДЭКАЭДР
- 21. Четвертая группа Архимедовых тел: КУРНОСЫЙ КУБ
- 22. КУРНОСЫЙ ДОДЕКАЭДР
- 23. Пятая группа Архимедовых тел состоит из одного многогранника: ПСЕВДОРОМБОКУБООКТАЭДР
- 24. Также существуют звёздчатые многогранники Звёздчатый многогранник (звёздчатое
- 25. 1. ЗВЁЗДЧАТЫЙ ОКТАЭДР 2.ЗВЁЗДЧАТЫЕ ФОРМЫ ДОДЕКАЭДРА
- 26. 3.ЗВЁЗДЧАТАЯ ФОРМА ИКОСАЭДРА
- 27. 4.ЗВЁЗДЧАТАЯ ФОРМА КУБООКТАЭДРА 5.ЗВЁЗДЧАТАЯ ФОРМА ИКОСОДОДЕКАЭДРА
- 28. Спасибо за внимание!
Слайд 3 Правильный многогранник или платоновое тело — это выпуклый многогранник с максимально возможной симметрией. Многогранник называется правильным, если: -он выпуклый; -все
Слайд 4Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники,
Платон
около 428 – 347 гг до н.э.
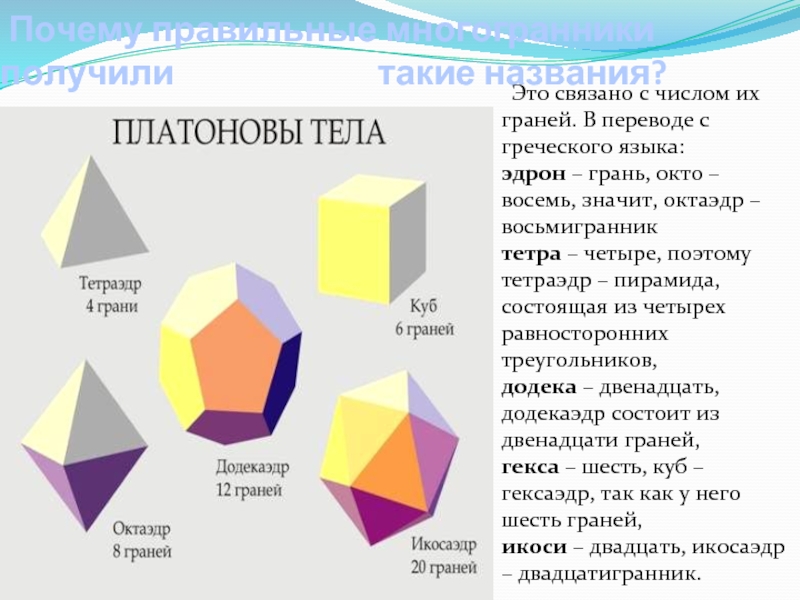
Слайд 5 Почему правильные многогранники получили
Это связано с числом их граней. В переводе с греческого языка:
эдрон – грань, окто – восемь, значит, октаэдр – восьмигранник
тетра – четыре, поэтому тетраэдр – пирамида, состоящая из четырех равносторонних треугольников,
додека – двенадцать, додекаэдр состоит из двенадцати граней,
гекса – шесть, куб – гексаэдр, так как у него шесть граней,
икоси – двадцать, икосаэдр – двадцатигранник.
Слайд 11Полуправильные многогранники - определение может варьироваться и включать различные типы многогранников, но
Полуправильные многогранники
Слайд 12Множество Архимедовых тел можно разбить на пять групп. Первую из них составляют
УСЕЧЕННЫЙ КУБ
Слайд 17 Вторую группу Архимедовых тел составляют два тела, именуемых квазиправильными многогранниками.
КУБООКТАЭДР
Слайд 24Также существуют звёздчатые многогранники
Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого
Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам.
Правильные звёздчатые многогранники - это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Существует всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера-Пуансо.