д.ф.-м.н. Потемкин И.И.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Микрофазное расслоение в расплаве двойных гребнеобразных сополимеров презентация
Содержание
- 1. Микрофазное расслоение в расплаве двойных гребнеобразных сополимеров
- 2. Микрофазное расслоение Диблок-сополимер 1
- 3. Микрофазное расслоение: Классические устойчивые морфологии ламеллярная цилиндрическая сферическая гироид 2
- 4. Микрофазное расслоение: Возможные области применения периодических структур
- 5. Основные подходы в теоретическом изучении микрофазного
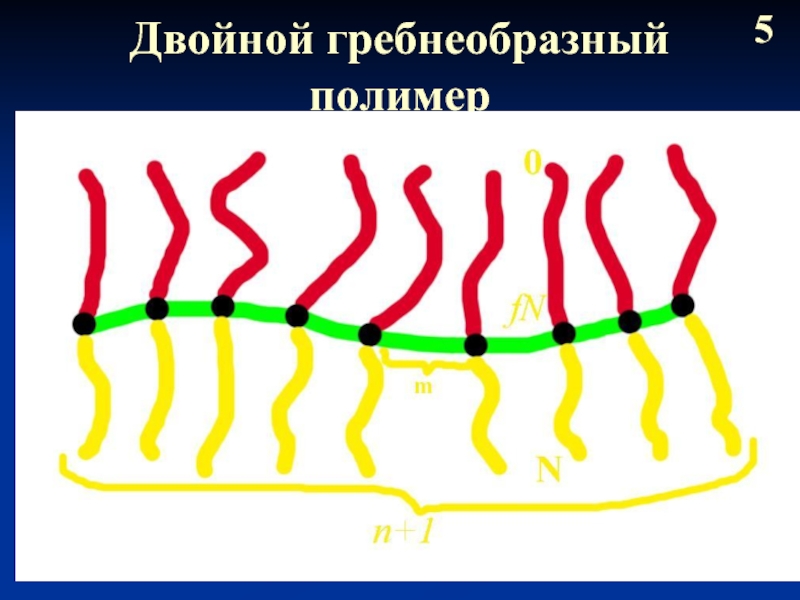
- 6. Двойной гребнеобразный полимер 5
- 7. Синтез двойных гребнеобразных полимеров
- 8. Основные предположения при теоретическом анализе задачи Слабая
- 9. 1. Плотнопривитой блок-сополимер (m = 1): 1.1
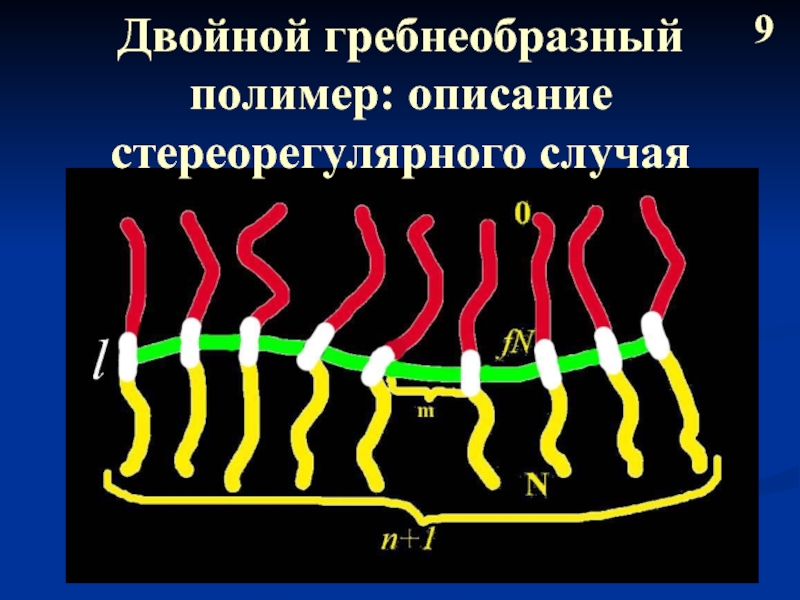
- 10. Двойной гребнеобразный полимер: описание стереорегулярного случая 9
- 11. 10 1. Плотнопривитой блок-сополимер (m = 1):
- 12. 1. Плотнопривитой блок-сополимер (m = 1): Стереорегулярный
- 13. 1. Плотнопривитой блок-сополимер (m = 1): Стереорегулярный
- 14. 2. Случай m ≠1: χAB= χ BС=
- 15. 2. Случай m ≠1: χAB= χ BС=
- 16. 2. Случай m ≠1: χAB= χ BС=
- 17. 2. Случай m ≠1: χAB= χ BС=
- 18. Выводы Исследован переход из однородного состояния в
- 19. Выводы Исследованы все случаи, в которых взаимодействия
- 20. Аналитические результаты 19
- 21. Аналитические результаты , где 20
Микрофазное расслоение
Диблок-сополимер 1
Слайд 1Микрофазное расслоение в расплаве двойных гребнеобразных сополимеров
В.В. Палюлин
Научный руководитель:
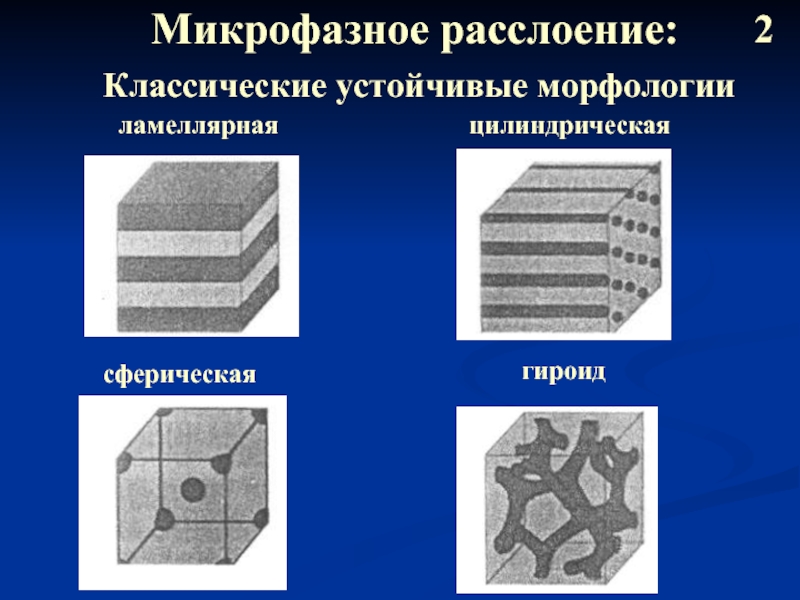
Слайд 3Микрофазное расслоение:
Классические устойчивые морфологии
ламеллярная
цилиндрическая
сферическая
гироид
2
Слайд 4Микрофазное расслоение:
Возможные области применения периодических структур
1. Создание систем с высокой плотностью
записи информации
2. Использование структур в качестве шаблонов для упаковки наночастиц
3. Изготовление фотонных кристаллов
2. Использование структур в качестве шаблонов для упаковки наночастиц
3. Изготовление фотонных кристаллов
3
Park C., Yoon J., Thomas E.L., Enabling nanotechnology with self-assembled block-copolymer patterns. Polymer, 2003, 44, 6725-6760
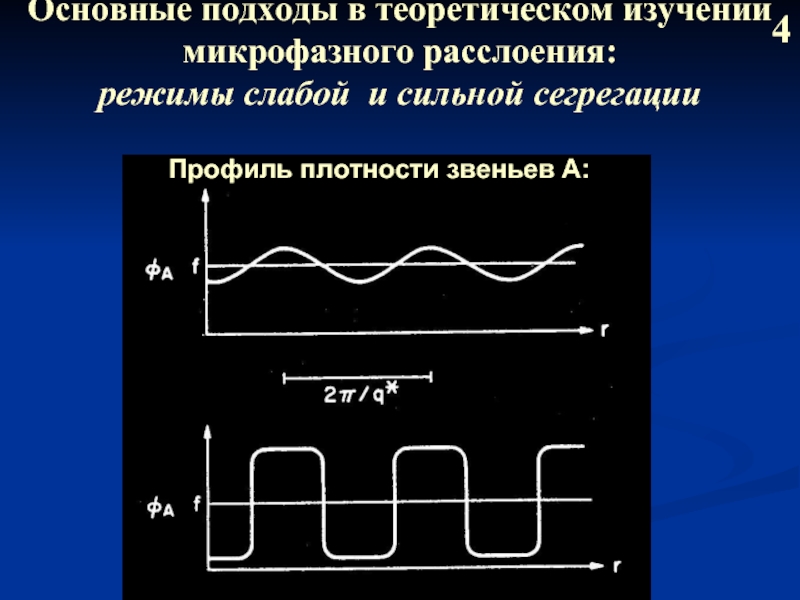
Слайд 5Основные подходы в теоретическом изучении микрофазного расслоения: режимы слабой и сильной
сегрегации
4
Профиль плотности звеньев A:
Слайд 7Синтез двойных гребнеобразных полимеров
Zhu Y., Weildisch R.,
Gido S.P., Velis G., Hadjichristidis N., Morphologies and Mechanical Properties of a Series of Block-Double-Graft Copolymers and Terpolymers. Macromolecules, 2002, 35, 5903-5909
6
Слайд 8Основные предположения
при теоретическом анализе задачи
Слабая сегрегация
Одинаковые размеры звеньев
Взаимодействия звеньев описываются параметрами
χij
Расчет произведен в ПСФ (квадратичное приближение)
Расчет произведен в ПСФ (квадратичное приближение)
7
Слайд 91. Плотнопривитой блок-сополимер (m = 1):
1.1 Стереорегулярный случай
1.2 Нестереорегулярный случай
2. Случай
m ≠ 1. Рассмотрены все 5 случаев, в которых взаимодействия описываются одним параметром Флори-Хаггинса
8
Слайд 1110
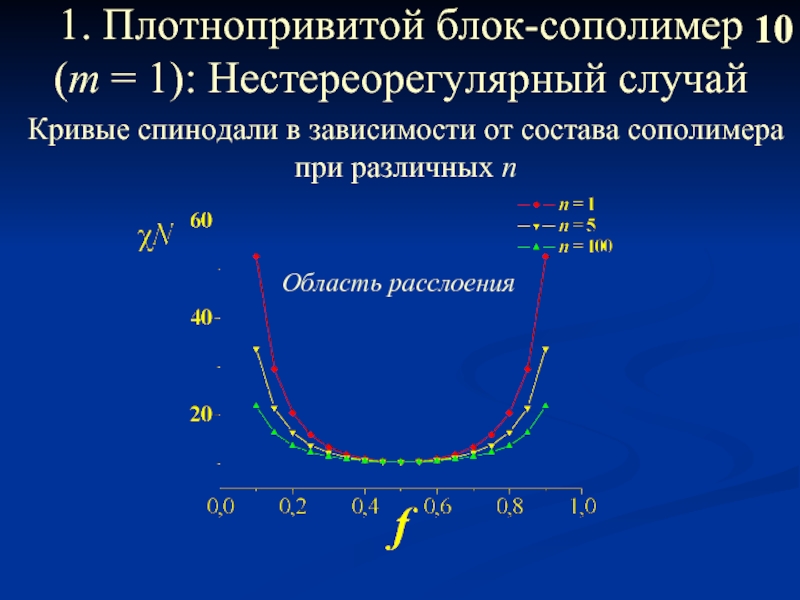
1. Плотнопривитой блок-сополимер (m = 1): Нестереорегулярный случай
Кривые спинодали в зависимости
от состава сополимера
при различных n
при различных n
Область расслоения
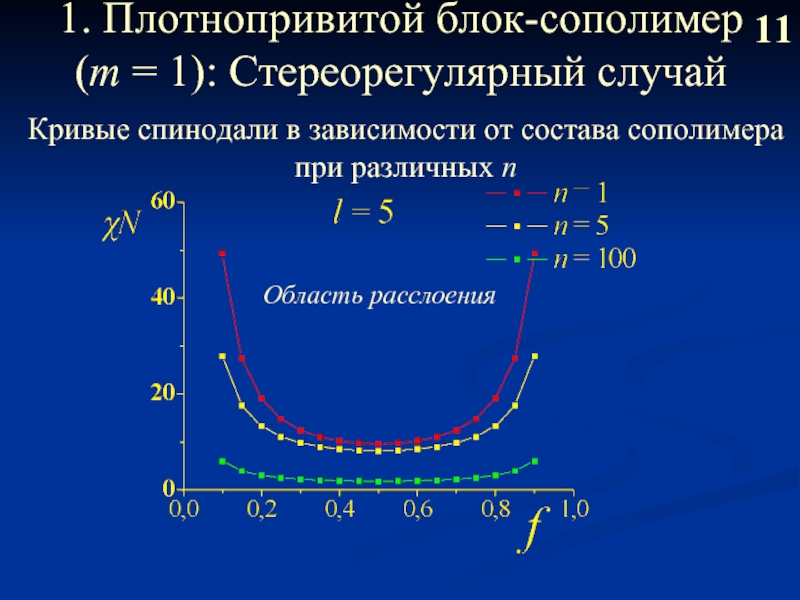
Слайд 121. Плотнопривитой блок-сополимер (m = 1): Стереорегулярный случай
11
Кривые спинодали в зависимости
от состава сополимера
при различных n
при различных n
Область расслоения
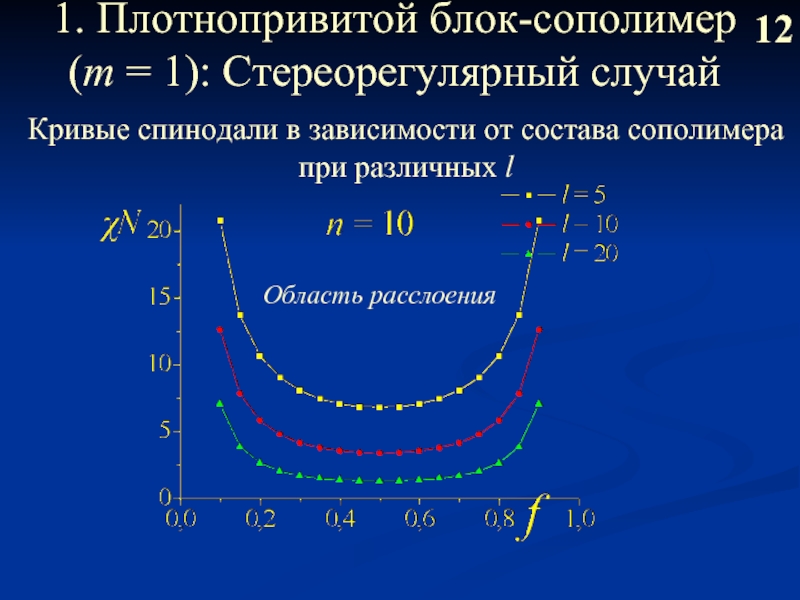
Слайд 131. Плотнопривитой блок-сополимер (m = 1): Стереорегулярный случай
12
Кривые спинодали в зависимости
от состава сополимера
при различных l
при различных l
Область расслоения
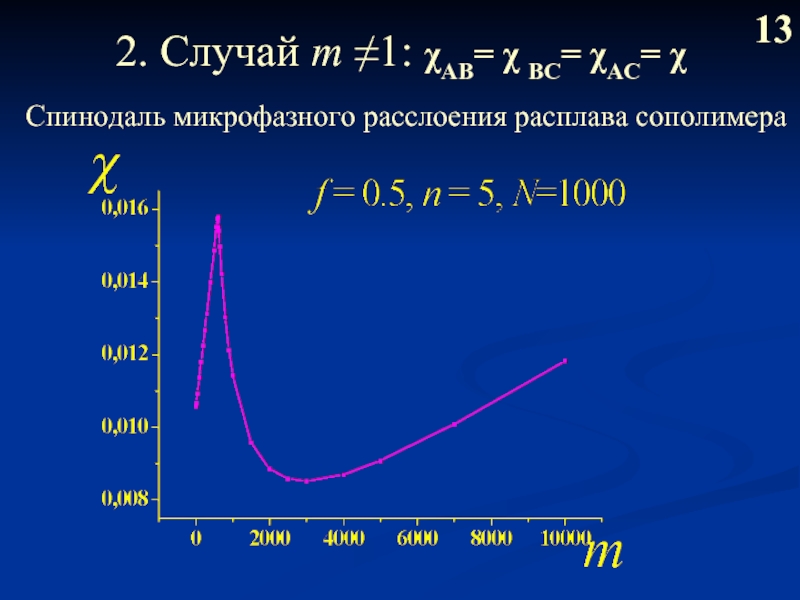
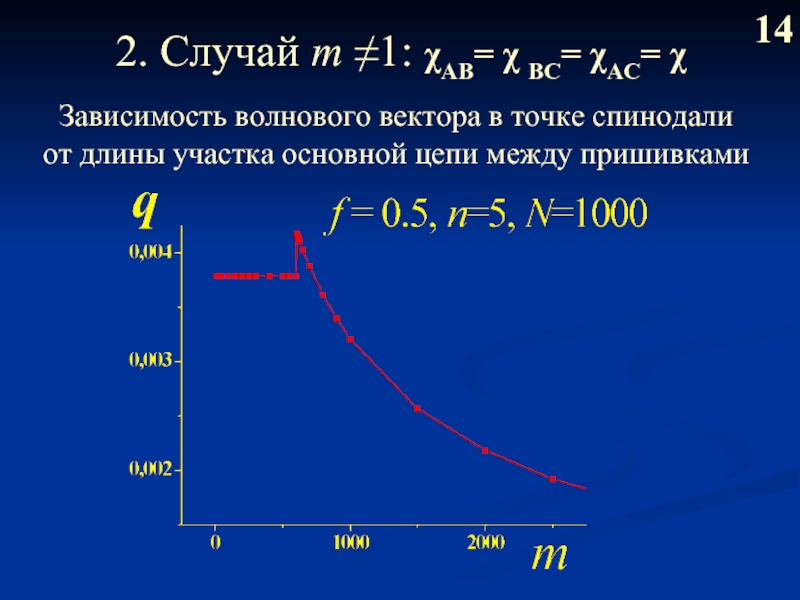
Слайд 152. Случай m ≠1: χAB= χ BС= χAC= χ
14
Зависимость волнового вектора
в точке спинодали
от длины участка основной цепи между пришивками
от длины участка основной цепи между пришивками
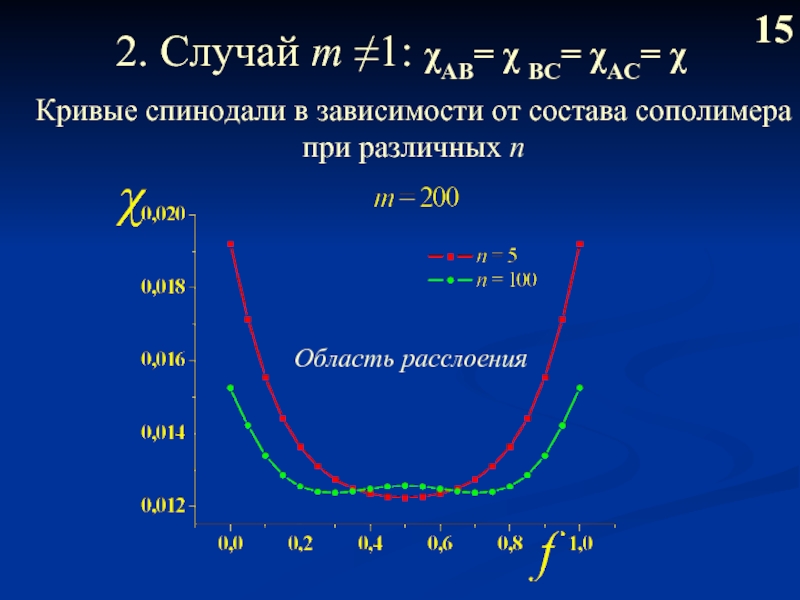
Слайд 162. Случай m ≠1: χAB= χ BС= χAC= χ
15
Кривые спинодали в
зависимости от состава сополимера
при различных n
при различных n
Область расслоения
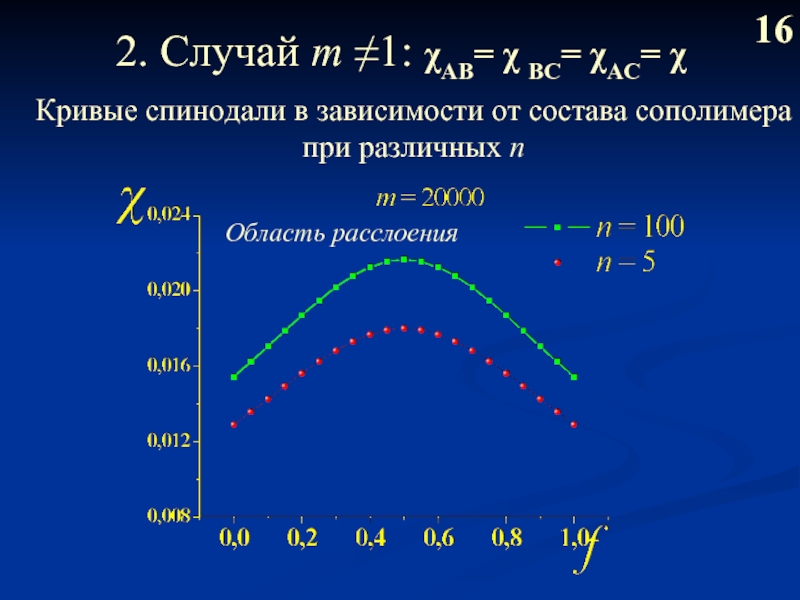
Слайд 172. Случай m ≠1: χAB= χ BС= χAC= χ
16
Кривые спинодали в
зависимости от состава сополимера
при различных n
при различных n
Область расслоения
Слайд 18Выводы
Исследован переход из однородного состояния в упорядоченное для плотной пришивки боковых
цепей.
В случае стереорегулярного расположения цепей поведение системы при росте n меняется по сравнению с нестереорегулярным случаем: вне зависимости от состава при росте n χN в точке перехода уменьшается.
В случае стереорегулярного расположения цепей поведение системы при росте n меняется по сравнению с нестереорегулярным случаем: вне зависимости от состава при росте n χN в точке перехода уменьшается.
17
Слайд 19Выводы
Исследованы все случаи, в которых взаимодействия описываются одним параметром Флори-Хаггинса при
m ≠ 1.
Построены спинодали и зависимости волнового вектора в точке перехода от параметров задачи и проведена интерпретация данных зависимостей.
Обнаружена возможность существования явления двухмасштабной неустойчивости в расплавах двойных гребнеобразных полимеров
Построены спинодали и зависимости волнового вектора в точке перехода от параметров задачи и проведена интерпретация данных зависимостей.
Обнаружена возможность существования явления двухмасштабной неустойчивости в расплавах двойных гребнеобразных полимеров
18
