- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы моделирования систем и процессов управления презентация
Содержание
- 1. Методы моделирования систем и процессов управления
- 2. Понятие модели. Назначение моделей. Виды моделей. Уровни
- 3. МОДЕЛЬ Модель – (французское modele, от латинского
- 4. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 5. СУЩНОСТЬ МОДЕЛИРОВНИЯ
- 6. ОБЩИЕ ПОДХОДЫ К МОДЕЛИРОВАНИЮ
- 7. ИЗОМОРФНЫЕ СИСТЕМЫ
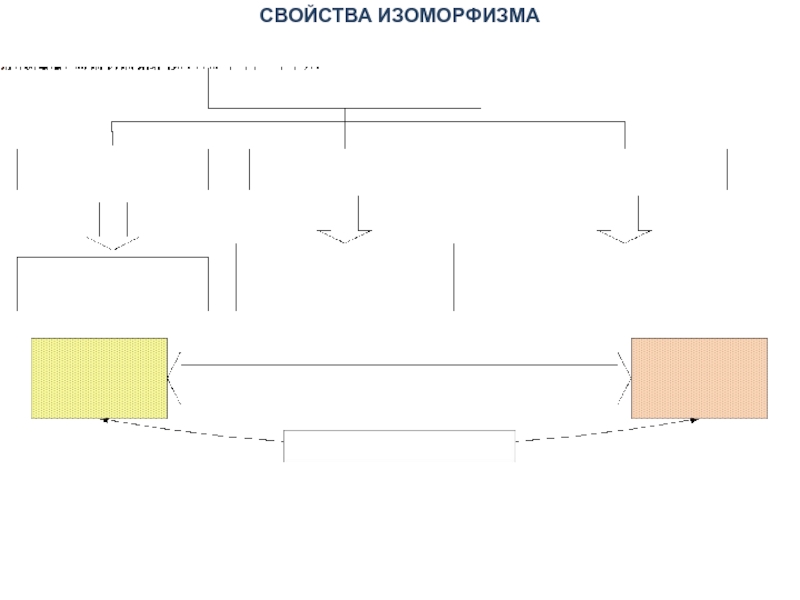
- 8. СВОЙСТВА ИЗОМОРФИЗМА
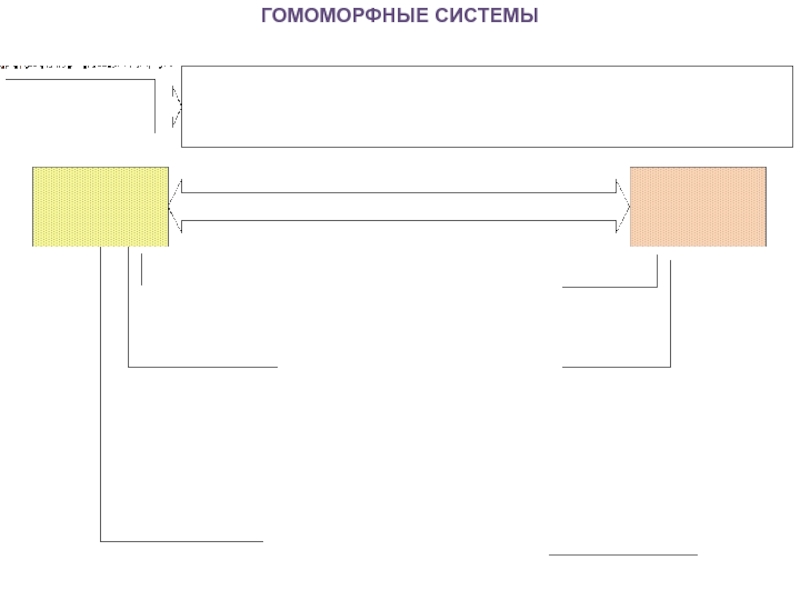
- 9. ГОМОМОРФНЫЕ СИСТЕМЫ
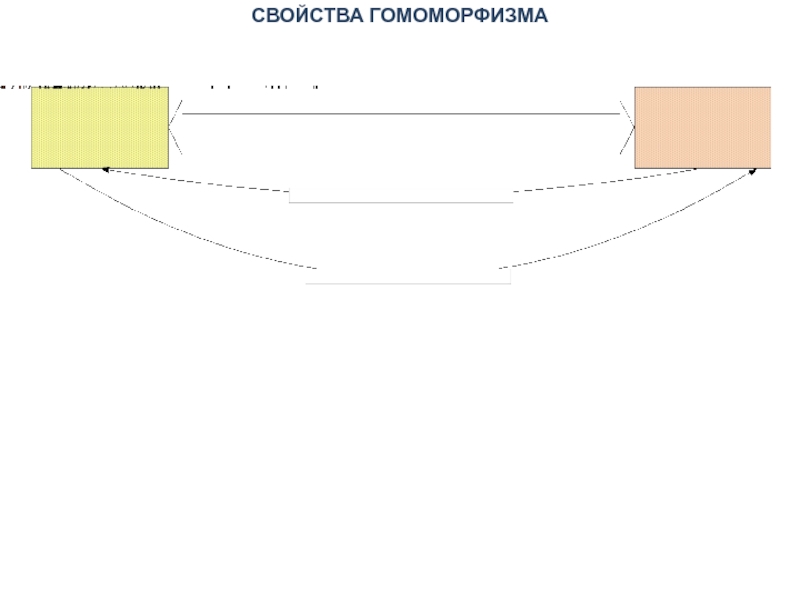
- 10. СВОЙСТВА ГОМОМОРФИЗМА
- 11. ПОДХОДЫ ПРИ МОДЕЛИРОВАНИИ ГОМОМОРФНЫМИ МОДЕЛЯМИ
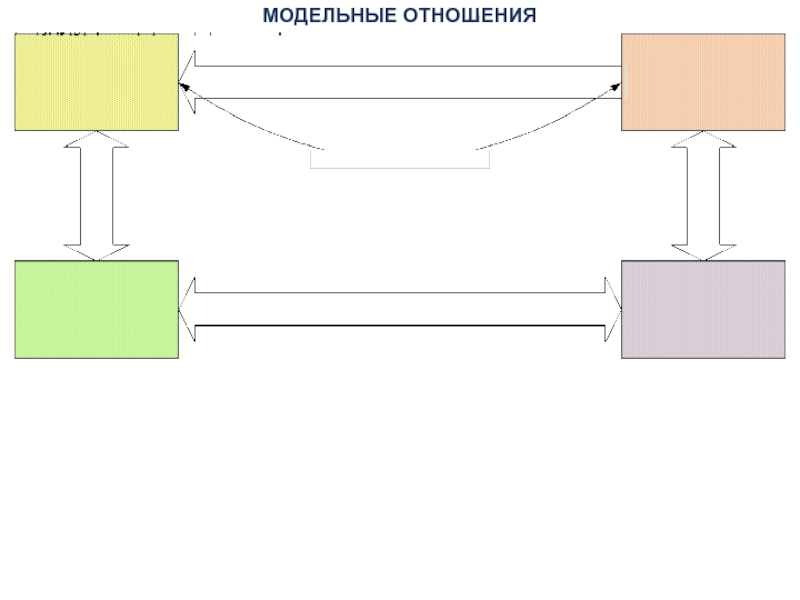
- 12. МОДЕЛЬНЫЕ ОТНОШЕНИЯ
- 13. ОСНОВНЫЕ ЦЕЛИ И ПРИНЦИПЫ МОДЕЛИРОВАНИЯ
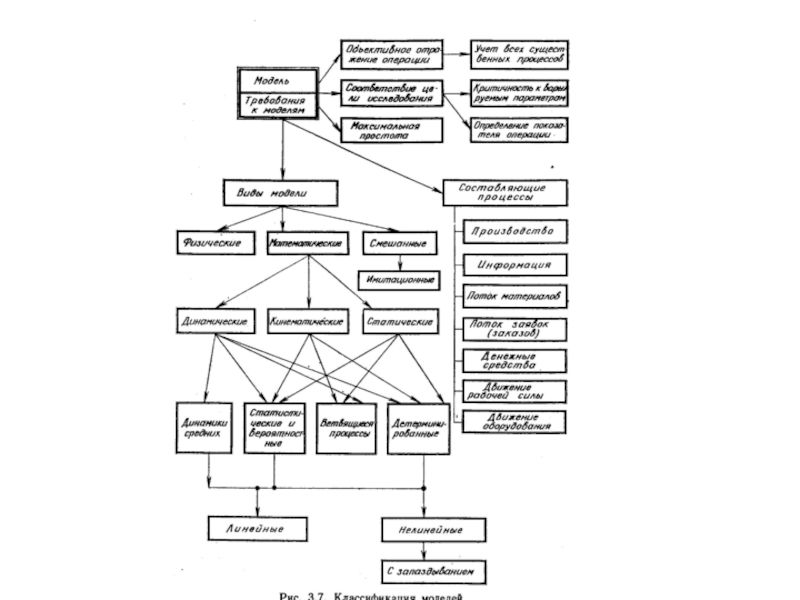
- 14. ТРЕБОВАНИЯ К МОДЕЛЯМ
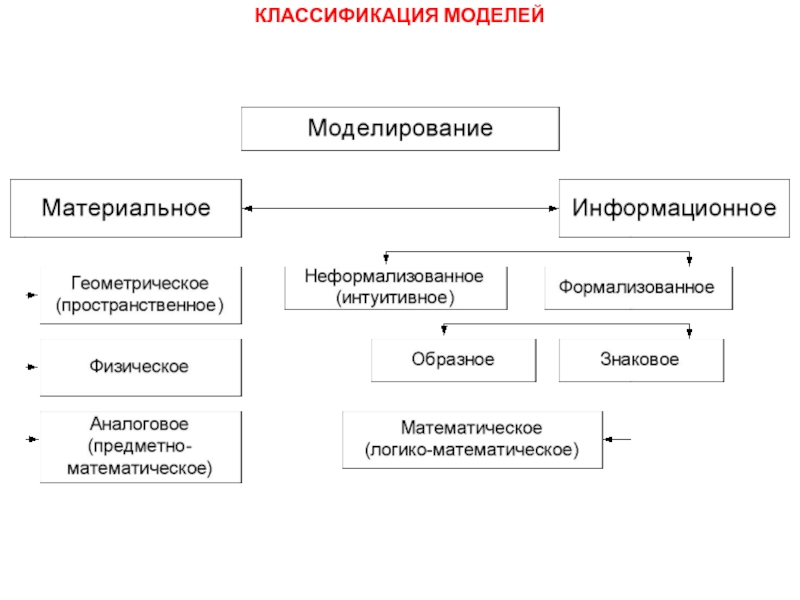
- 15. КЛАССИФИКАЦИЯ МОДЕЛЕЙ
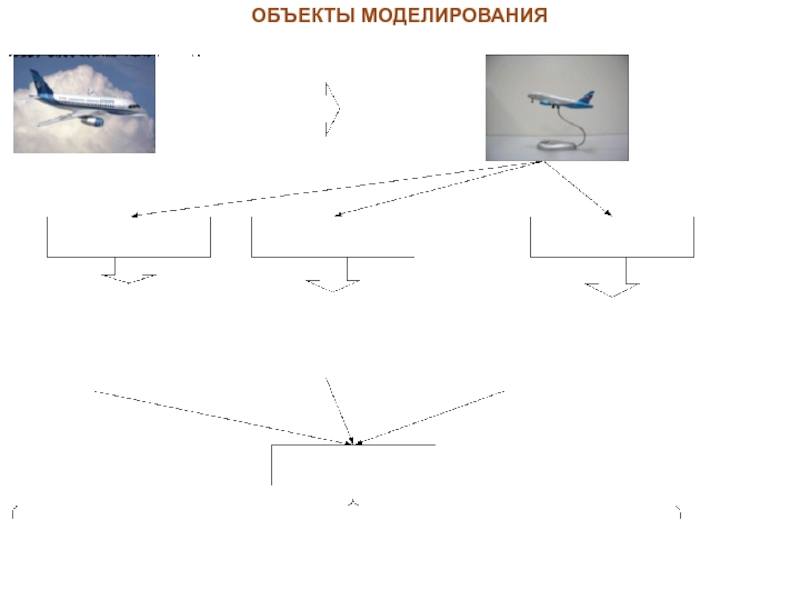
- 18. ОБЪЕКТЫ МОДЕЛИРОВАНИЯ
- 19. УРОВНИ МОДЕЛИРОВАНИЯ
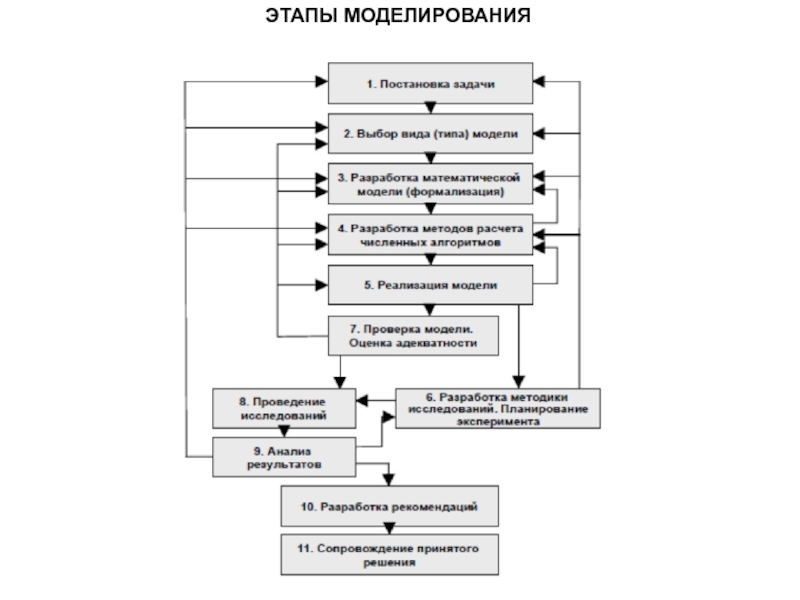
- 20. ЭТАПЫ МОДЕЛИРОВАНИЯ
- 21. ЭТАПЫ МОДЕЛИРОВАНИЯ
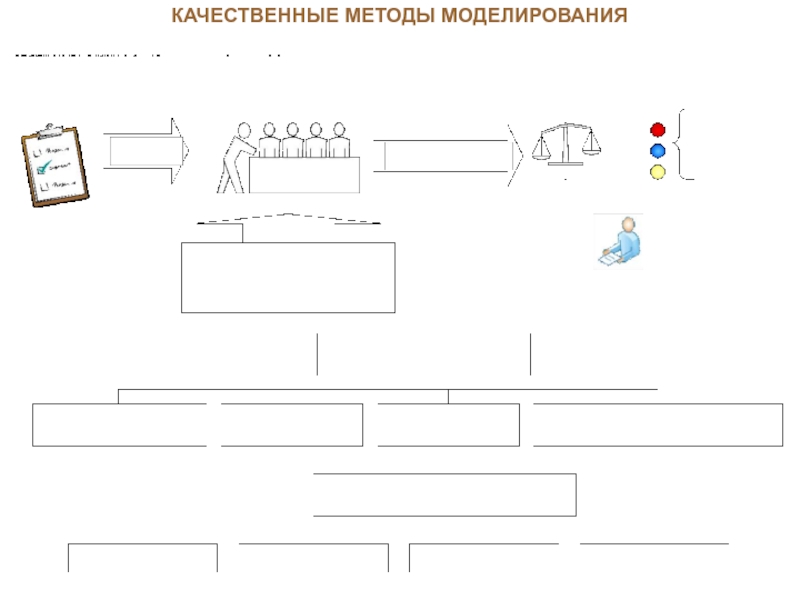
- 23. КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
- 24. КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
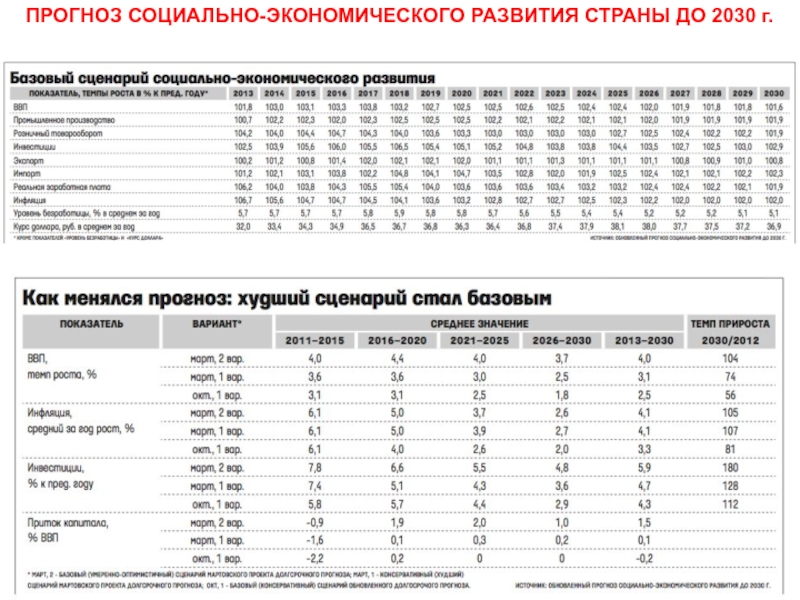
- 25. ПРОГНОЗ СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ СТРАНЫ ДО 2030 г.
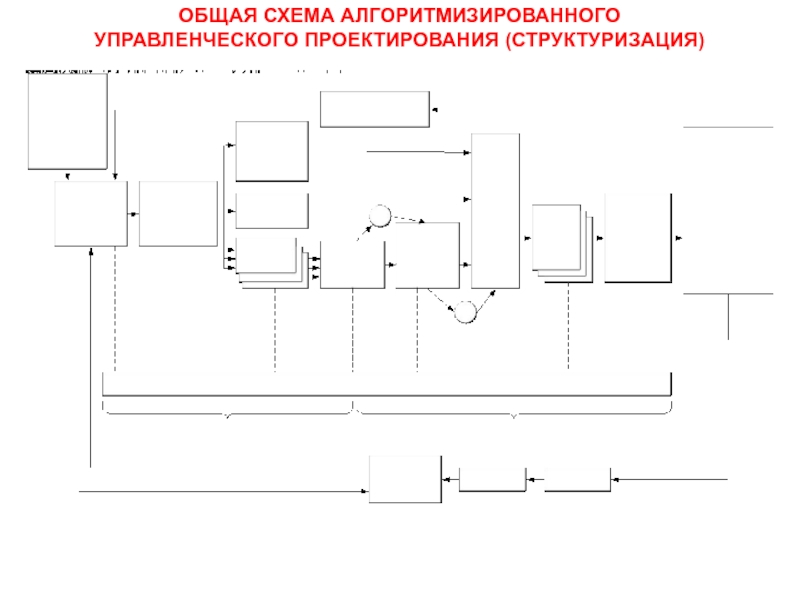
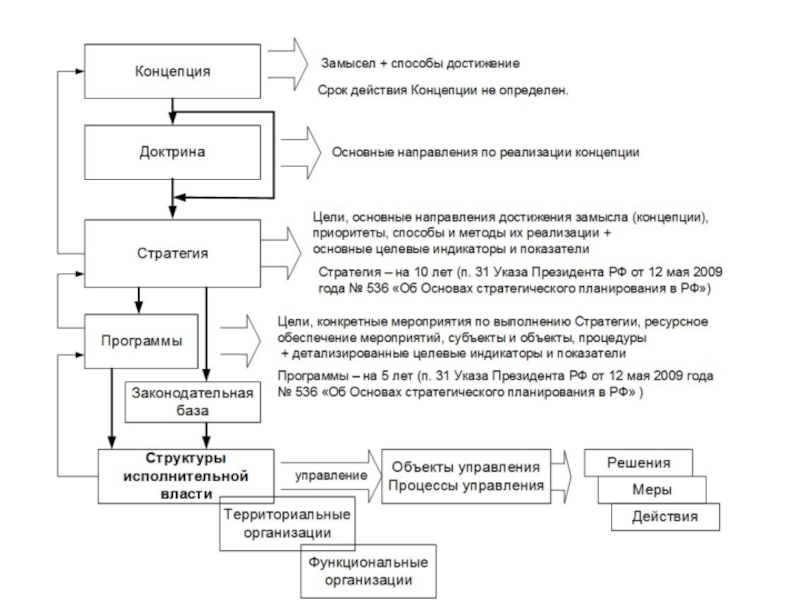
- 26. ОБЩАЯ СХЕМА АЛГОРИТМИЗИРОВАННОГО УПРАВЛЕНЧЕСКОГО ПРОЕКТИРОВАНИЯ (СТРУКТУРИЗАЦИЯ)
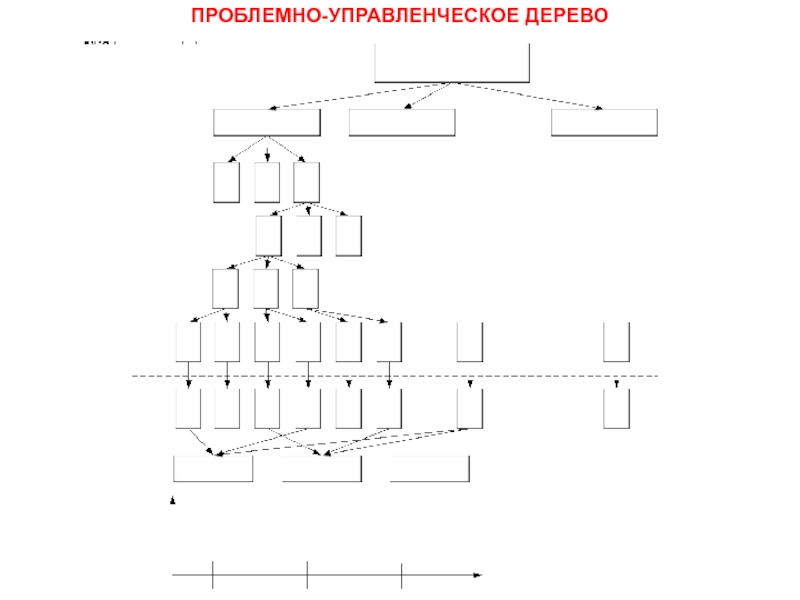
- 27. ПРОБЛЕМНО-УПРАВЛЕНЧЕСКОЕ ДЕРЕВО
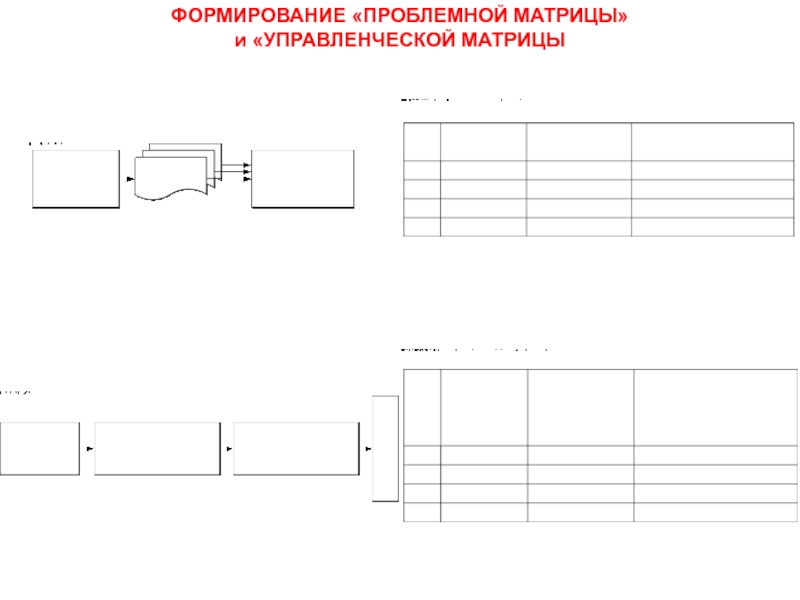
- 28. ФОРМИРОВАНИЕ «ПРОБЛЕМНОЙ МАТРИЦЫ» и «УПРАВЛЕНЧЕСКОЙ МАТРИЦЫ
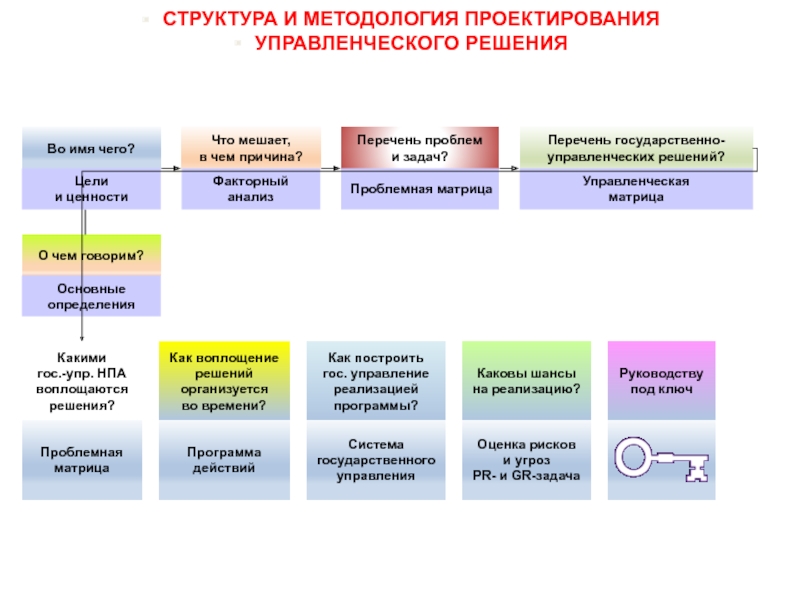
- 29. СТРУКТУРА И МЕТОДОЛОГИЯ ПРОЕКТИРОВАНИЯ УПРАВЛЕНЧЕСКОГО РЕШЕНИЯ
- 33. КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
- 34. КАЧЕСТВЕННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ
- 35. СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ (для дискретных случайных величин)
- 36. СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ (для непрерывных случайных величин) Закон
- 37. АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Процессы функционирования системы записываются в
- 38. ТЕОРЕТИКО-МНОЖЕСТВЕННОЕ ПРЕДСТАВЛЕНИЕ Понятия: множество, элементы множества, отношения
- 39. МНОЖЕСТВО И ПОДМНОЖЕСТВО Схема представлений
- 40. ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ
Слайд 2Понятие модели.
Назначение моделей.
Виды моделей.
Уровни моделирования.
Классификации методов моделирования систем.
Аналитические и статистические методы.
Математическая
Содержание занятия
Слайд 3МОДЕЛЬ
Модель – (французское modele, от латинского modulus - мера, образец).
1.
2. В широком смысле – любой образ, аналог (мысленный или условный: изображение, описание, схема, чертеж, график, план, карта и т.п.) какого-либо объекта, процесса или явления («оригинала» данной модели), используемый в качестве его «заместителя», «представителя».
3. В математике и логике моделью какой-либо системы аксиом называют любую совокупность (абстрактных) объектов, свойства которых и отношения между которыми удовлетворяют данным аксиомам, служащим тем самым совместным (неявным) определением такой совокупности.
4. Модель в языкознании - абстрактное понятиев языкознании - абстрактное понятие эталона или образца какой-либо системы (фонологической, грамматической и т.п.), представление самых общих характеристик какого-либо языкового явления; общая схема описания системы языка или какой-либо его подсистемы
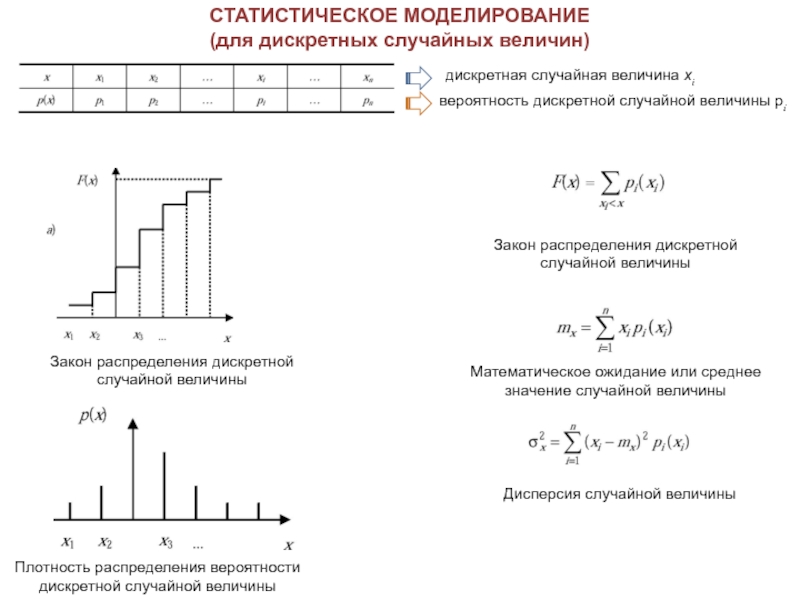
Слайд 35СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
(для дискретных случайных величин)
дискретная случайная величина хi
вероятность дискретной случайной величины
Закон распределения дискретной случайной величины
Плотность распределения вероятности дискретной случайной величины
Математическое ожидание или среднее значение случайной величины
Дисперсия случайной величины
Закон распределения дискретной случайной величины
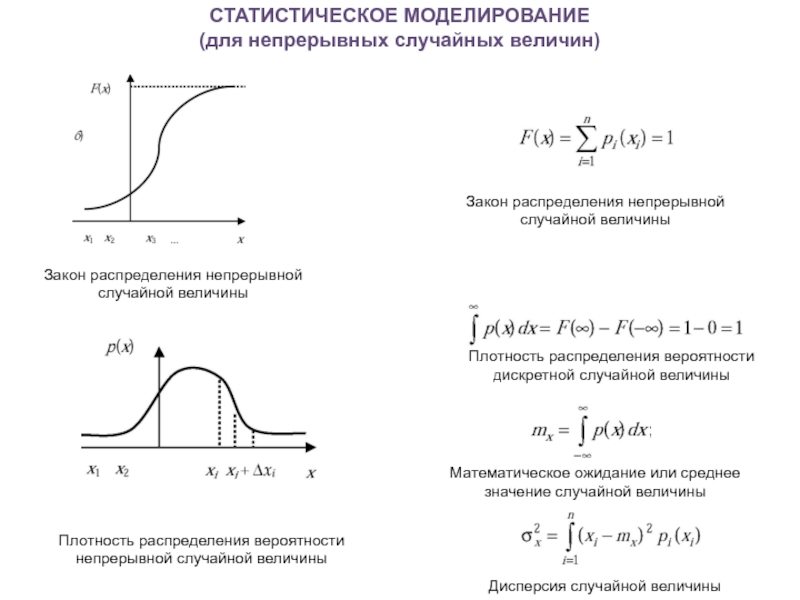
Слайд 36СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
(для непрерывных случайных величин)
Закон распределения непрерывной случайной величины
Плотность распределения вероятности
Плотность распределения вероятности дискретной случайной величины
Математическое ожидание или среднее значение случайной величины
Дисперсия случайной величины
Закон распределения непрерывной случайной величины
Слайд 37АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Процессы функционирования системы записываются в виде некоторых функциональных соотношений: алгебраических,
Аналитическая модель может быть исследована следующими методами:
1) аналитическим, когда стремятся получить в общем виде явные зависимости для характеристик систем;
2) численным, когда не удается найти решение уравнений в общем виде и их решают для конкретных начальных данных;
3) качественным, когда при отсутствии решения находят некоторые его свойства.
Слайд 38ТЕОРЕТИКО-МНОЖЕСТВЕННОЕ ПРЕДСТАВЛЕНИЕ
Понятия: множество, элементы множества, отношения на множествах.
Понятие множество относится к
Это понятие содержательно эквивалентно понятиям «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «класс» и другим обобщающим понятиям.
Множества могут задаваться следующими способами:
1. Списком, перечислением (интенсиональным путём);
или
2. Путём указания некоторого характеристического свойства А (экстенсионально).
Например, «множество натуральных чисел», «множество рабочих данного завода», «множество планет солнечной системы», «множество А» и т.д.
или
свертывание
Слайд 39МНОЖЕСТВО И ПОДМНОЖЕСТВО
Схема представлений
теоретико-множественных моделей
Пустое множество - множество, в котором