- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИКА В СТРАНАХ ИСЛАМА -ГЕОМЕТРИЯ презентация
Содержание
- 1. МАТЕМАТИКА В СТРАНАХ ИСЛАМА -ГЕОМЕТРИЯ
- 2. Арабский мир
- 3. Культурной столицей исламского мира первоначально был Багдад,
- 4. Исследования мусульман в геометрии основывались на
- 5. ТЕОРИЯ ПАРАЛЛЕЛЬНЫХ внимание арабских ученых привлекла теория
- 6. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ: ТЕОРИЯ ПАРАЛЛЕЛЬНЫХ В СВЯЗИ С ПОПЫТКАМИ ДОКАЗАТЬ V ПОСТУЛАТ ЕВКЛИДА.
- 7. Многие полагали, что содержащееся в этом постулате
- 8. САБИТ ИБН КОРРА астроном, математик и врач
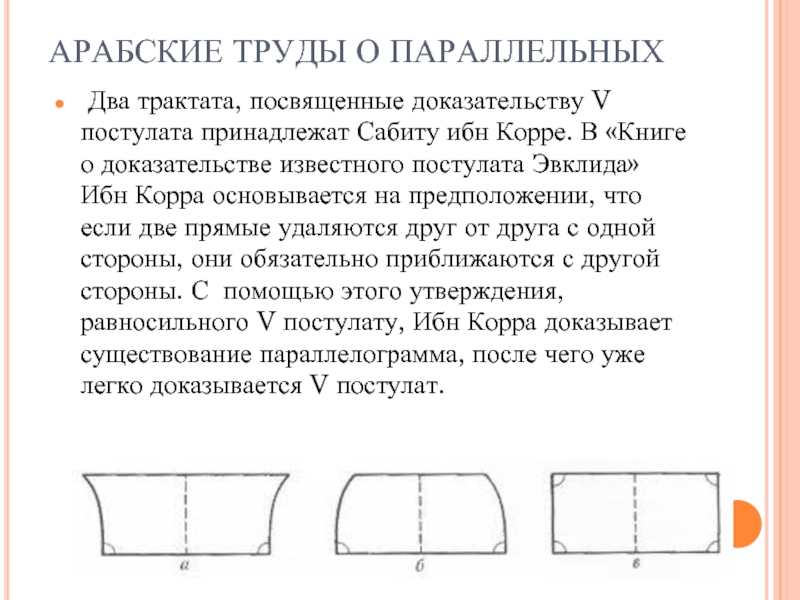
- 9. АРАБСКИЕ ТРУДЫ О ПАРАЛЛЕЛЬНЫХ Два трактата,
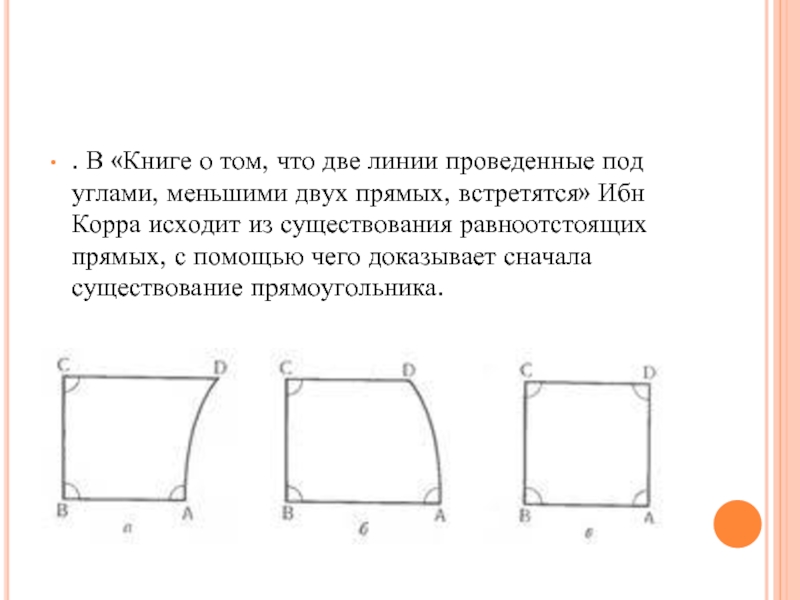
- 10. . В «Книге о том, что две
- 11. ИБН АЛЬ-ХАЙСАМ великий арабский учёный,
- 12. В «Книге комментариев к введениям в «Начала» Евклида
- 13. ОМАР ХАЙЯМ Омар глубоко занимался математикой, астрономией,
- 14. ГЕОМЕТРИЯ В ТРУДАХ ОМАР ХАЙЯМ Омар
- 15. Для нужд землемерия, архитектуры, техники разрабатывались и методы геометрических построений.
- 16. ИБН КОРРЫ ИБРАХИМ ИБН СИНАН известный математик,
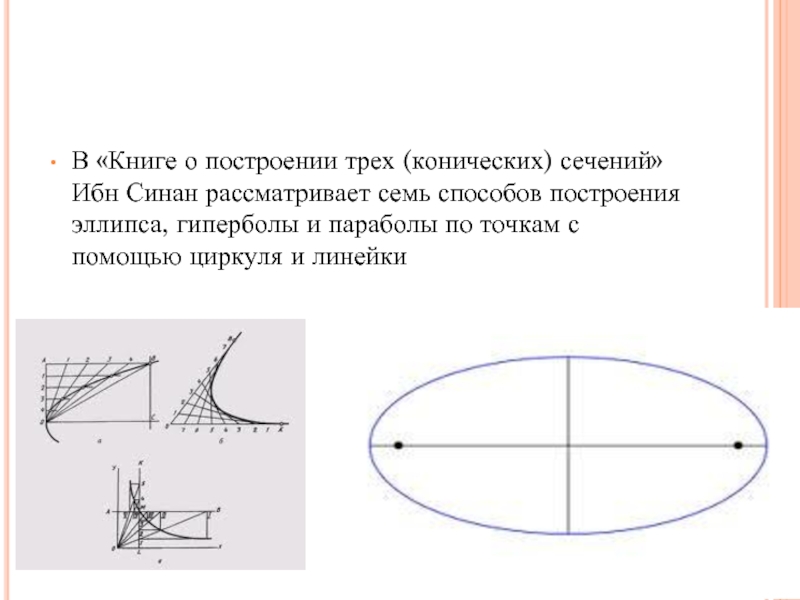
- 17. В «Книге о построении трех (конических) сечений»
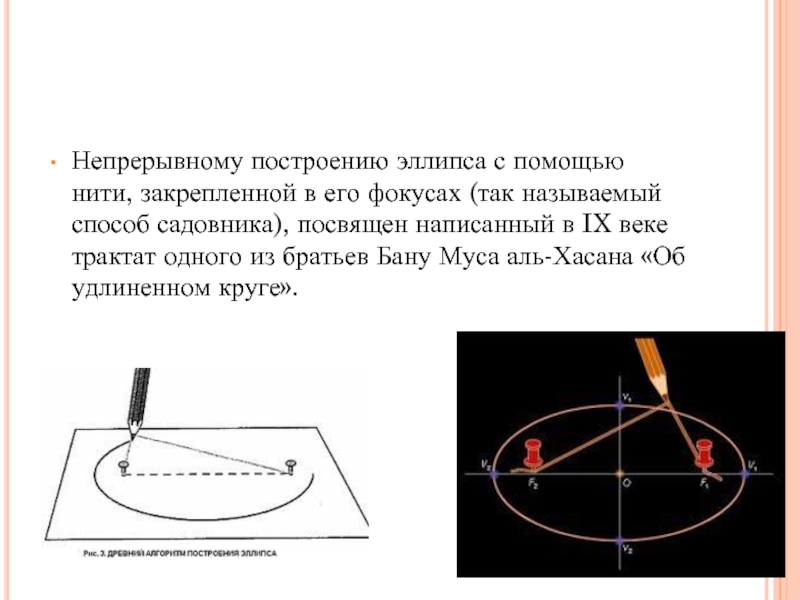
- 18. Непрерывному построению эллипса с помощью нити, закрепленной
- 19. АБУ-Л-ВАФЫ один из крупнейших математиков и астрономов
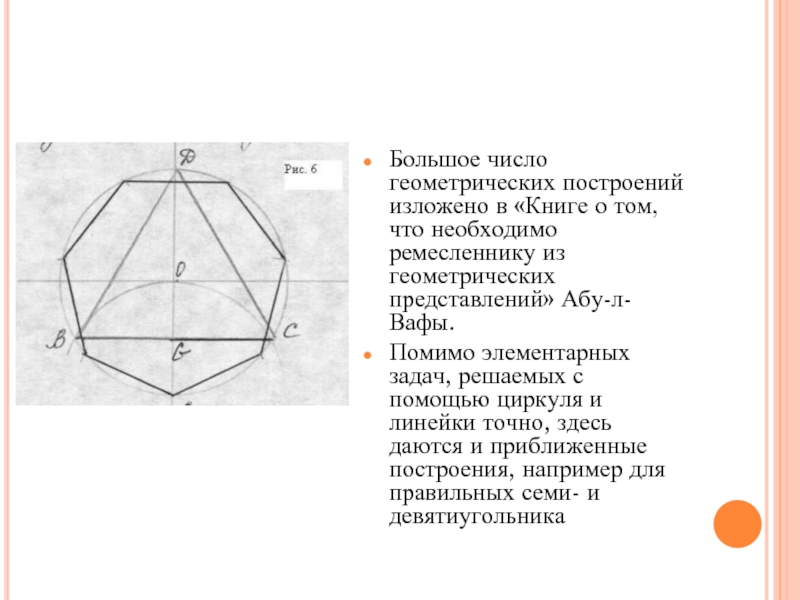
- 20. Большое число геометрических построений изложено в «Книге
- 21. АЛ-ХОРЕЗМИ Основоположником алгебры, как особой науки,
- 22. ВОПРОСЫ ГЕОМЕТРИИ В ТРУДАХ АЛ-ХОРЕЗМИ В геометрическом
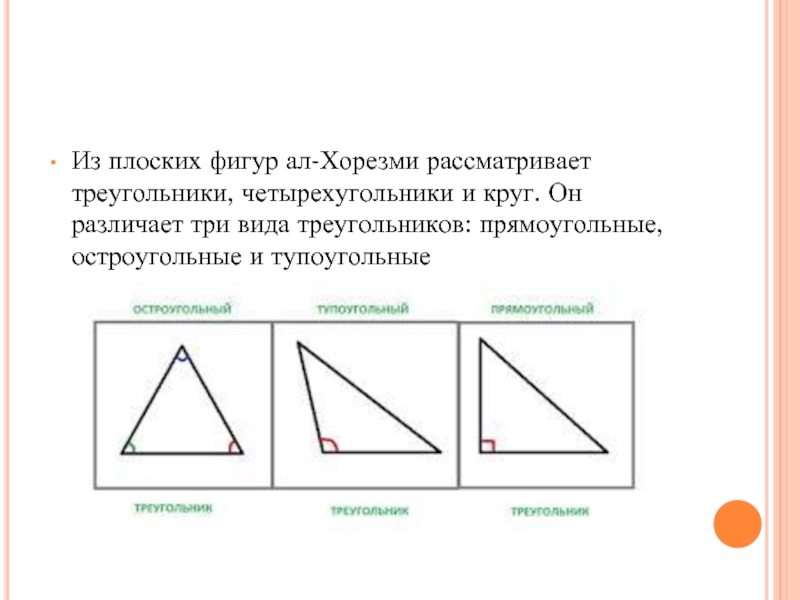
- 23. Из плоских фигур ал-Хорезми рассматривает треугольники, четырехугольники
- 24. Абу Сахл аль-Кухи был одним из группы
- 25. Абу Сахл аль-Кухи при помощи теории конических
- 26. Геометрия играла важную роль в работе мусульманских
- 27. Одним из таких параметров было золотое сечение,
- 28. Золотое сечение так названо потому, что если
- 29. ИСКУССТВО И АРАБЕСКИ. Геометрическое искусство представляет
- 31. Арабеска – это узор, составленный из нескольких
- 32. «Арабеска старается не привлекать внимание к определённому
- 33. Страны ислама известны геометрическими узорами, украшающими их
Слайд 3Культурной столицей исламского мира первоначально был Багдад, где халифы создают «Дом
Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, поставила и сама религия ислама.
Слайд 4
Исследования мусульман в геометрии основывались на трёх столпах эллин. Первый –
Слайд 5ТЕОРИЯ ПАРАЛЛЕЛЬНЫХ
внимание арабских ученых привлекла теория параллельных. Постулат параллельных Эвклида (если
Слайд 6ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ: ТЕОРИЯ ПАРАЛЛЕЛЬНЫХ В СВЯЗИ С ПОПЫТКАМИ ДОКАЗАТЬ V ПОСТУЛАТ
Слайд 7Многие полагали, что содержащееся в этом постулате утверждение является теоремой, которую
Слайд 8САБИТ ИБН КОРРА
астроном, математик и врач IX века .По происхождению сириец,
Слайд 9АРАБСКИЕ ТРУДЫ О ПАРАЛЛЕЛЬНЫХ
Два трактата, посвященные доказательству V постулата принадлежат
Слайд 10. В «Книге о том, что две линии проведенные под углами,
Слайд 11 ИБН АЛЬ-ХАЙСАМ
великий арабский учёный, упомянуты 92 сочинения Ибн ал-Хайсама,
Слайд 12В «Книге комментариев к введениям в «Начала» Евклида Ибн ал-Хайсам пытался доказать пятый
Слайд 13ОМАР ХАЙЯМ
Омар глубоко занимался математикой, астрономией, философией. Он блестяще закончил курс
Слайд 14 ГЕОМЕТРИЯ В ТРУДАХ ОМАР ХАЙЯМ
Омар Хайям в «Комментариях к трудностям
Слайд 15
Для нужд землемерия, архитектуры, техники разрабатывались и методы геометрических построений.
Слайд 16ИБН КОРРЫ ИБРАХИМ ИБН СИНАН
известный математик, внук Сабита ибн Корры. Ему принадлежат «Книга
посвятил теории геометрических построений специальную «Книгу о методе анализа и синтеза и о других действиях в геометрических задачах».
Слайд 17В «Книге о построении трех (конических) сечений» Ибн Синан рассматривает семь
Слайд 18Непрерывному построению эллипса с помощью нити, закрепленной в его фокусах (так
Слайд 19АБУ-Л-ВАФЫ
один из крупнейших математиков и астрономов средневекового Востока. . Абу аль-Вафа
Слайд 20Большое число геометрических построений изложено в «Книге о том, что необходимо
Помимо элементарных задач, решаемых с помощью циркуля и линейки точно, здесь даются и приближенные построения, например для правильных семи- и девятиугольника
Слайд 21АЛ-ХОРЕЗМИ
Основоположником алгебры, как особой
науки, нужно считать среднеазиатского
ученого Мухаммеда из Хорезма
известного
аль-Хваризми (Хорезмиец).
Значительный период своей жизни он провёл в Багдаде, возглавляя библиотеку «Дома мудрости»
Слайд 22ВОПРОСЫ ГЕОМЕТРИИ В ТРУДАХ АЛ-ХОРЕЗМИ
В геометрическом отделе алгебры ал-Хорезми собраны правила
Слайд 23Из плоских фигур ал-Хорезми рассматривает треугольники, четырехугольники и круг. Он различает
Слайд 24Абу Сахл аль-Кухи был одним из группы одарённых учёных восточной территории
Слайд 25Абу Сахл аль-Кухи при помощи теории конических сечений смог разработать метод
Абу Сахл аль-Кухи работал и над созданием «совершенного циркуля», нового прибора, который мог быть использован для чертежа конических сечений.
Абу Сахл также известен открытием метода деления угла на три равные части.
Слайд 26Геометрия играла важную роль в работе мусульманских художников, архитекторов и каллиграфов.
Слайд 27Одним из таких параметров было золотое сечение, которое радует глаз и
Слайд 28Золотое сечение так названо потому, что если отрезок делился, то соотношение
Слайд 29ИСКУССТВО И АРАБЕСКИ.
Геометрическое искусство представляет собой слияние чистой математики и искусства
Слайд 31Арабеска – это узор, составленный из нескольких объединённых и переплетённых друг
Слайд 32«Арабеска старается не привлекать внимание к определённому объекту, не оживлять и
Б. Добре, историк искусства,