- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика и живопись презентация
Содержание
- 1. Математика и живопись
- 2. Цели: изучение математических законов, влияющих на изобразительное
- 3. Пропорция Пропорция - равенство отношений числовых величин,
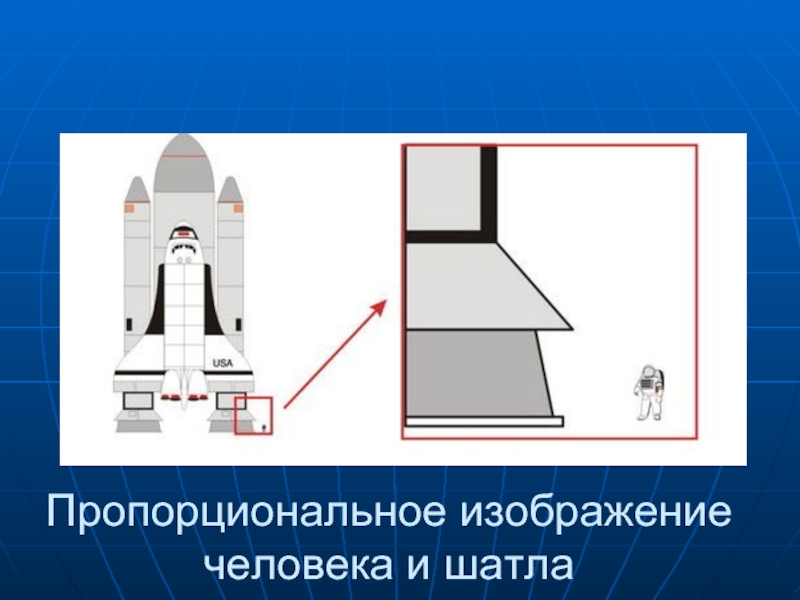
- 4. Пропорциональное изображение человека и шатла
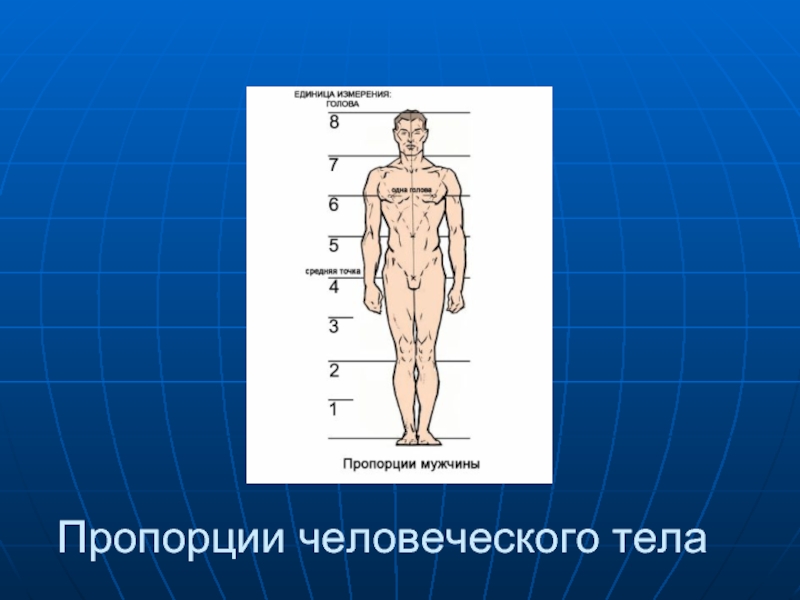
- 5. Пропорции человеческого тела
- 6. Соотношение пропорций человека в разном возрасте
- 7. Золотое сечение Золотое сечение - деление непрерывной
- 8. Египетские пирамиды – пример золотого сечения в архитектуре
- 9. Пушкин на лицейском экзамене в Царском Селе.
- 10. Сильные точки При изображении объектов на картине
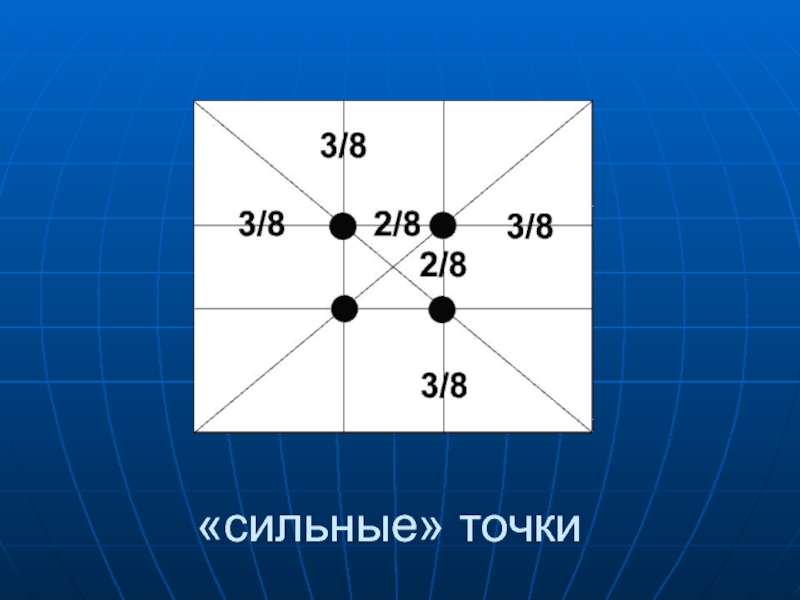
- 11. «сильные» точки
- 12. «сильные» точки на картине И.И. Шишкина и К.А. Савицкого «Утро в сосновом лесу»
- 13. Золотое сечение в теле человека Пропорции тела
- 14. Витрувианский человек
- 15. Золотое сечение в человеческом теле
- 16. фракталы Фрактал - термин, означающий сложную геометрическую
- 17. Пример Фрактала
- 18. Пример фрактала в природе
- 19. Фрактальное изображение
- 20. Перспектива Перспектива - Явление кажущегося искажения пропорций
- 21. Прямая линейная перспектива Прямая линейная перспектива -
- 22. Обратная линейная перспектива Обратная линейная перспектива -
- 23. аксонометрия Аксонометрия - один из видов перспективы,
- 24. Невозможные фигуры Невозможная фигура - эти фигура,
- 25. мосты, которые не могут существовать в трехмерном пространстве
- 26. Невозможный куб
- 27. проецирование Проецирование - изображение трёхмерной фигуры на
- 28. проецирование
- 29. Тень
- 30. Симметрия Симметрия - Две точки А и
- 31. Осевая симметрия, это по сути дела, отражение, которое активно применяется в живописи.
- 32. Но применение симметрии в живописи не ограничивается отражением. Практически все орнаменты - семетричны
- 33. Заключение В данной работе рассмотрено только несколько
Слайд 2Цели: изучение математических законов, влияющих на изобразительное искусство
Задачи: Найти элементы
математики, влияющие на живопись.
Изучить влияние выявленных элементов на живопись.
Изучить влияние выявленных элементов на живопись.
Слайд 3Пропорция
Пропорция - равенство отношений числовых величин, т. е. равенство вида a :
b = c : d
Одной из задач при изображении объектов является изобразить их соразмерно, то есть пропорционально.
Одной из задач при изображении объектов является изобразить их соразмерно, то есть пропорционально.
Слайд 7Золотое сечение
Золотое сечение - деление непрерывной величины на две части в
таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Отношение частей в этой пропорции выражается квадратичной иррациональностью и примерно равно 1.628033887
Отношение частей в этой пропорции выражается квадратичной иррациональностью и примерно равно 1.628033887
Слайд 10Сильные точки
При изображении объектов на картине важно правильно их расположить. На
первый взгляд было бы расположить объект по середине , но это не так. Наиболее гармоничными смотрятся объекты, расположенными согласно золотому сечению. Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.
Слайд 13Золотое сечение в теле человека
Пропорции тела человека соответствуют золотому сечению.
Например, если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.
Слайд 16фракталы
Фрактал - термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то
есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения.
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения.
Слайд 20Перспектива
Перспектива - Явление кажущегося искажения пропорций и формы тел при их
визуальном наблюдении.
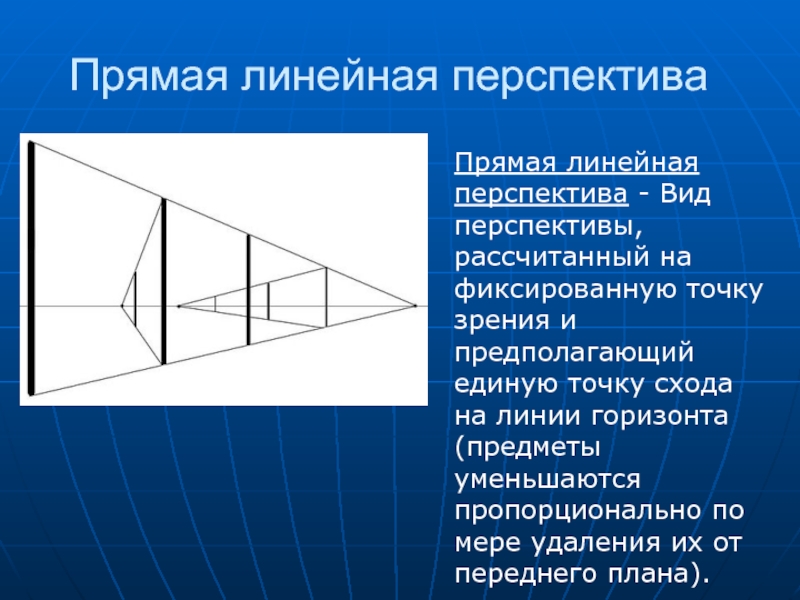
Слайд 21Прямая линейная перспектива
Прямая линейная перспектива - Вид перспективы, рассчитанный на фиксированную
точку зрения и предполагающий единую точку схода на линии горизонта (предметы уменьшаются пропорционально по мере удаления их от переднего плана).
Слайд 22Обратная линейная перспектива
Обратная линейная перспектива - Вид перспективы, применяемый в византийской
и древнерусской живописи, при которой изображенные предметы представляются увеличивающимися по мере удаления от зрителя
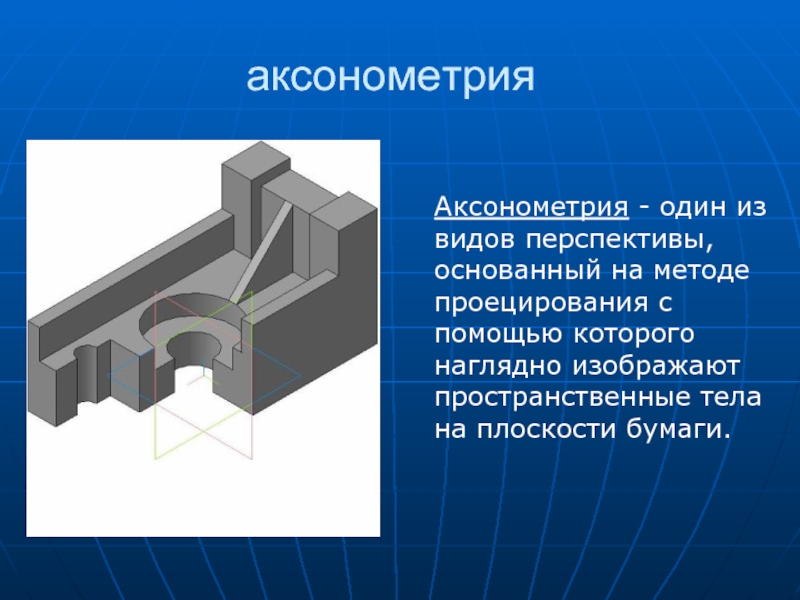
Слайд 23аксонометрия
Аксонометрия - один из видов перспективы, основанный на методе проецирования с
помощью которого наглядно изображают пространственные тела на плоскости бумаги.
Слайд 24Невозможные фигуры
Невозможная фигура - эти фигура, изображенная в перспективе таким способом,
чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве
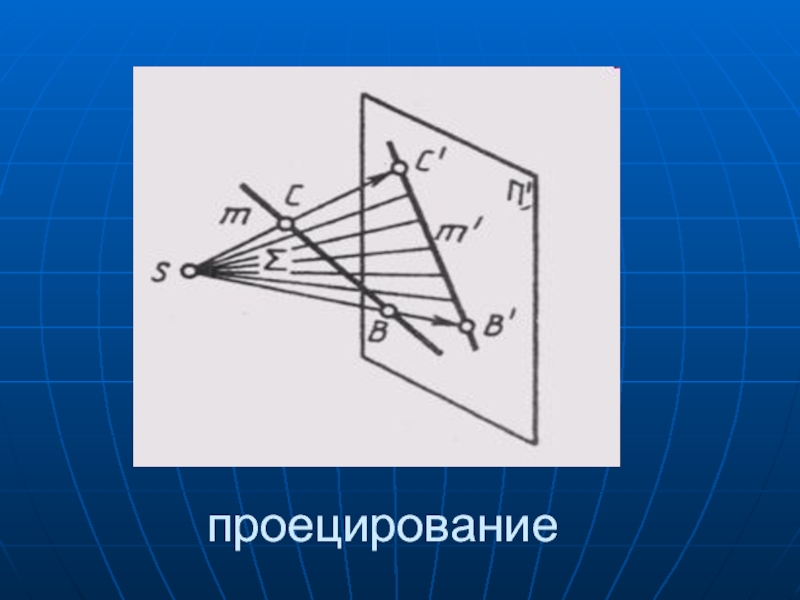
Слайд 27проецирование
Проецирование - изображение трёхмерной фигуры на так называемой проекционной плоскости
Суть проецирования
в следующем, надо выбрать плоскость, которую назовем плоскостью проекций. Перед ней поместим любой объект. Перед объектом расположим центр проецирования, из которого направим к плоскости проекций проецирующие лучи через все точки объекта до пересечения их с плоскостью проекций. На плоскости проекций получим изображение совокупности точек, которое будет являться проекцией данного обьекта.
Слайд 30Симметрия
Симметрия - Две точки А и А1 называется симметричными относительно точки
О, если О – середина АА1. Точка считается симметричной самой себе.
Симметрия бывает:
Осевая
Центральная
Зеркальная
Поворотная
Переносная
Криволинейная
Симметрия подобия
Симметрия бывает:
Осевая
Центральная
Зеркальная
Поворотная
Переносная
Криволинейная
Симметрия подобия
Слайд 32Но применение симметрии в живописи не ограничивается отражением. Практически все орнаменты -
семетричны
Слайд 33Заключение
В данной работе рассмотрено только несколько законов математики, применяемых живописцами. Но
этого уже достаточно, чтобы убедиться во взаимосвязи двух на первый взгляд несовместимых понятий: математика и живопись.
Основываясь на расчетах, используя геометрические законы, применяя математические методы, компьютерную графику и художники, и дизайнеры создают для нас такие произведения искусств, которые улучшают эмоциональное и психологическое состояние человека.
В ходе работы по данной теме выяснилось, что математика не только «ум в порядок приводит», но и несет в себе большой эстетический потенциал в развитии различных видов искусства, являясь «царицей всех наук».
Основываясь на расчетах, используя геометрические законы, применяя математические методы, компьютерную графику и художники, и дизайнеры создают для нас такие произведения искусств, которые улучшают эмоциональное и психологическое состояние человека.
В ходе работы по данной теме выяснилось, что математика не только «ум в порядок приводит», но и несет в себе большой эстетический потенциал в развитии различных видов искусства, являясь «царицей всех наук».