операциям арифметического сложения и сдвигу кодов.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Машинные коды чисел презентация
Содержание
- 1. Машинные коды чисел
- 2. Прямой машинный код Прямой код целого числа
- 3. Два представления нуля В системе прямых кодов
- 4. Дополнительный и обратный коды Замена операции вычитания
- 5. Дополнительный код отрицательного числа Пример. А=9510,
- 6. Дополнительный код отрицательного числа Дополнительный код
- 7. Модуль числа представить прямым кодом в
- 8. Примеры. 1. Дано отрицательное целое десятичное число
- 9. 2. Дано целое число в виде 16-ричного
- 10. 2 способ: через 16-ричную систему счисления
- 11. Действия над машинными кодами целых чисел Дано:
- 12. Действия над машинными кодами чисел с фиксированной
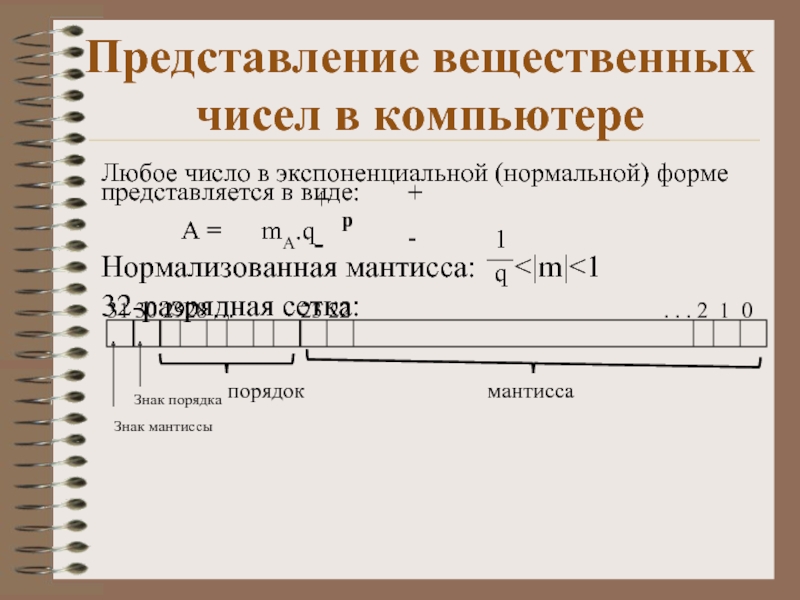
- 13. Представление вещественных чисел в компьютере Знак мантиссы Знак порядка порядок мантисса
- 14. В современных компьютерах машинная форма числа хранит
- 15. Нормализованная мантисса всегда имеет целый разряд 0
- 16. Для записи внутреннего представления вещественного числа
- 17. Примеры Найдем нормализованные мантиссы и характеристики этих
- 18. б) B= -32008,5= -7D08,816= - 0,7D088.164 mB=
- 20. Действия над числами, представленными в экспоненциальной
- 21. Примеры Выполнить операцию сложения машинных
- 22. PA+B = 3 A+B = 0.F29ED.103 = F29,ED16=
Прямой машинный код Прямой код целого числа полностью совпадает с записью самого числа в разрядной сетке компьютера. Прямой код отрицательного целого числа отличается от прямого кода соответствующего положительного числа содержимым знакового
Слайд 2Прямой машинный код
Прямой код целого числа полностью совпадает с записью самого
числа в разрядной сетке компьютера. Прямой код отрицательного целого числа отличается от прямого кода соответствующего положительного числа содержимым знакового разряда
Пример. Прямой код чисел Х=110112 и Y=-110112 в восьмиразрядной сетке имеет вид:
[Xпк]=00011011
[Yпк]=10011011
Пример. Прямой код чисел Х=110112 и Y=-110112 в восьмиразрядной сетке имеет вид:
[Xпк]=00011011
[Yпк]=10011011
Слайд 3Два представления нуля
В системе прямых кодов существует два различных представления ноля:
00000000 – положительный 0;
10000000 – отрицательный 0.
Оба представления совершенно равноправны.
10000000 – отрицательный 0.
Оба представления совершенно равноправны.
Слайд 4Дополнительный и обратный коды
Замена операции вычитания (алгебраического сложения) на арифметическое сложение
в компьютере осуществляется с помощью обратного и дополнительного кодов.
Дополнительный и обратный коды положительного числа совпадают с прямым кодом.
Дополнительный и обратный коды положительного числа совпадают с прямым кодом.
Слайд 5
Дополнительный код отрицательного числа
Пример. А=9510, В=4310, n=2. Найти С=А-В.
[-Bдк]=100 – 43
= 57
С = 95 + [-Bдк] – 100 = 95 + 57 – 100 = 152 – 100 = 52
Единицу в старшем разряде суммы можно просто зачеркивать, что равносильно сдвигу кода.
С = 95 + [-Bдк] – 100 = 95 + 57 – 100 = 152 – 100 = 52
Единицу в старшем разряде суммы можно просто зачеркивать, что равносильно сдвигу кода.
Слайд 6
Дополнительный код отрицательного числа
Дополнительный код получается путём добавления единицы к младшему
разряду обратного кода.
В дополнительном коде ноль имеет единственное представление. Для данной длины разрядной сетки дополнительным кодом представляется на единицу больше отрицательных чисел, чем положительных.
В дополнительном коде ноль имеет единственное представление. Для данной длины разрядной сетки дополнительным кодом представляется на единицу больше отрицательных чисел, чем положительных.
Слайд 7
Модуль числа представить прямым кодом в k двоичных разрядах.
Значения всех бит,
кроме знакового, инвертировать: все ноли заменить на единицы, а единицы на ноли (таким образом получается k-разрядный обратный код исходного числа);
К полученному обратному коду, прибавить единицу к младшему разряду с учетом переносов.
К полученному обратному коду, прибавить единицу к младшему разряду с учетом переносов.
Алгоритм получения дополнительного кода отрицательного числа.
Слайд 8Примеры.
1. Дано отрицательное целое десятичное число
M=-20. Представьте число в машинном
коде в 16-разрядной сетке в двоичной и 16-ричной системах счисления.
М=-20=-101002
[Mпк]2=1.000 0000 0001 0100
[M ок]2=1.111 1111 1110 1011
[M дк]2=1.111 1111 1110 1100
[M дк]16=FFEC
Слайд 92. Дано целое число в виде 16-ричного двоичного машинного кода. Определите
десятичное значение данного числа: Ka=FFD4
Первая цифра F, следовательно, число отрицательное и хранится в компьютере в форме дополнительного машинного кода.
FFD416 = [1.111 1111 1101 0100дк]
[1.111 1111 1101 0011ок] – обратный код числа
[Ka]ПК=[1.000 0000 0010 1100пк] – прямой двоичный код числа
Тогда десятичное число а = - 101100 = - (32+8+4) = -44 – десятичное число
-0.000 0000 0000 0001
Слайд 10
2 способ: через 16-ричную систему счисления
Ka=FFD4 < 0, следовательно число а
хранится в компьютере в дополнительном коде.
Перейдем от дополнительного к прямому машинному коду:
Так как дополнительный код для отрицательного числа равен дополнению его величины до числа, возникающего при переполнении разрядной сетки qn, то [Ka]ПК= 1000016 - FFD416 = 002С16
Тогда десятичное число а = - 2С16= - (2.161 + 12.160) =
= - 44
Перейдем от дополнительного к прямому машинному коду:
Так как дополнительный код для отрицательного числа равен дополнению его величины до числа, возникающего при переполнении разрядной сетки qn, то [Ka]ПК= 1000016 - FFD416 = 002С16
Тогда десятичное число а = - 2С16= - (2.161 + 12.160) =
= - 44
Слайд 11Действия над машинными кодами целых чисел
Дано: десятичные числа А= 34 и
В = 30
Найти: А+В, А – В, В – А в двоичных машинных
кодах в 8 разрядной сетке.
[Aпк] = [Аок] = [Адк] = 0.010 00102
[-Aпк] = 1.010 0010
[-Аок] = 1.101 1101
[-Адк] =1.101 1110
[-Bпк] =1.001 1110
[-Вок] = 1.110 0001
[-Вдк] = 1.110 0010
[Впк] = [Вок] = [Вдк] = 0.001 11102
Слайд 12Действия над машинными кодами чисел с фиксированной точкой ( в 16-ричной
системе счисления)
Дано: десятичные числа А= 34 и В = 30
Найти: А+В, А – В, В – А в 16-ричных машинных
кодах в 16 разрядной сетке.
1) А=34=2216 В=30=1E16
[KA]пк=002216 [KB]ПК=001E16
KA + KB = 0022 + 001E = 004016 ⇒ A + B =4.161 + 0.160 = 64
2) [K-B]ПК=101E16 [K-B]ДК=1000016 - 1E16 = FFE216
KA + KB = 0022 + FFE2 = 1 0004
А - В = 4.160 = 4
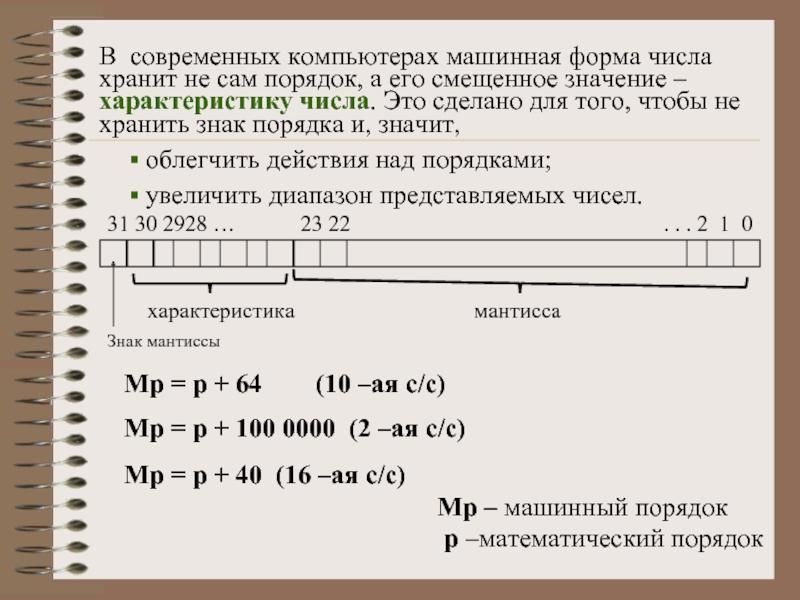
Слайд 14В современных компьютерах машинная форма числа хранит не сам порядок, а
его смещенное значение – характеристику числа. Это сделано для того, чтобы не хранить знак порядка и, значит,
облегчить действия над порядками;
увеличить диапазон представляемых чисел.
облегчить действия над порядками;
увеличить диапазон представляемых чисел.
Знак мантиссы
характеристика
мантисса
Мр = р + 64 (10 –ая с/c)
Мр = р + 100 0000 (2 –ая с/c)
Мр = р + 40 (16 –ая с/c)
Мр – машинный порядок
р –математический порядок
Слайд 15Нормализованная мантисса всегда имеет целый разряд 0 и, следовательно, этот 0
в памяти компьютера не хранится, а только подразумевается. Это полезное техническое решение позволяет увеличить количество цифр и, следовательно, точность вычислений.
Нормализованная мантисса числа 25.32410
0.25324 *102
Слайд 16
Для записи внутреннего представления вещественного числа необходимо:
Перевести модуль данного числа в 2-ую с.с. ( 16-ую с.с.),
Нормализовать двоичное число (16-ричное число),
Найти машинный порядок в 2-ой (16-ой с.с.),
Учитывая знак числа, выписать его представление в 32 разрядной сетке
Слайд 17Примеры
Найдем нормализованные мантиссы и характеристики этих чисел:
а) А=32008,5=7D08,816=0,7D088.164
mA=0,7D088 pxA=4+40=4416=10001002
Знак - 0
Характеристика - 1000100
Дробная часть -
0111 1101 0000 1000 1000 0000
мантиссы
KA= 0.1000100.0111 1101 0000 1000 1000 00002 = = 447D088016 > 0
мантиссы
KA= 0.1000100.0111 1101 0000 1000 1000 00002 = = 447D088016 > 0
Слайд 18б) B= -32008,5= -7D08,816= - 0,7D088.164
mB= -0,7D088 pxB=4+40=4416=10001002
Знак - 1
Характеристика - 1000100
Дробная часть - 0111
1101 0000 1000 1000 0000
мантиссы
KB= 1.1000100.0111 1101 0000 1000 1000 00002 = = C47D088016 < 0
мантиссы
KB= 1.1000100.0111 1101 0000 1000 1000 00002 = = C47D088016 < 0
Слайд 20Действия над числами, представленными
в экспоненциальной форме
Числа в экспоненциальной форме хранятся
в памяти в прямом коде с нормализованными мантиссами.
Сложение кодов производится путём сложения мантисс только при одинаковых порядках (характеристиках) слагаемых. За общий выбирается наибольший порядок.
Алгоритмы операции алгебраического сложения после выравнивания характеристик зависят от знаков слагаемых.
Результаты в прямом коде нормализуются.
Сложение кодов производится путём сложения мантисс только при одинаковых порядках (характеристиках) слагаемых. За общий выбирается наибольший порядок.
Алгоритмы операции алгебраического сложения после выравнивания характеристик зависят от знаков слагаемых.
Результаты в прямом коде нормализуются.
Слайд 21Примеры
Выполнить операцию сложения машинных кодов чисел А и В с
плавающей точкой в 32-хразрядной сетке. В качестве ответа записать код результата (в 2-ой и 16-ой с/с) и соответствующее этому коду десятичное число
Слайд 22PA+B = 3 A+B = 0.F29ED.103 = F29,ED16= 15.162+
2.161+9.160+14/16+13/256 = 3881 237/256
K
A+B =0.100 0011.1111 0010 1001 1110 1101 00002=
= 43.F29ED0
