- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Маршрут, цепь, цикл Маршрутом называют последовательность вершин и ребер, в которой любые два соседних элемента инцидентны (т.е. соединены). Например: презентация
Содержание
- 2. Маршрут, цепь, цикл
- 3. Маршрутом называют последовательность вершин и ребер, в
- 4. Если вершины v0 = vk, то маршрут
- 5. Если маршрут в простом графе задан последовательностью
- 6. Цепь - это маршрут, в котором нет
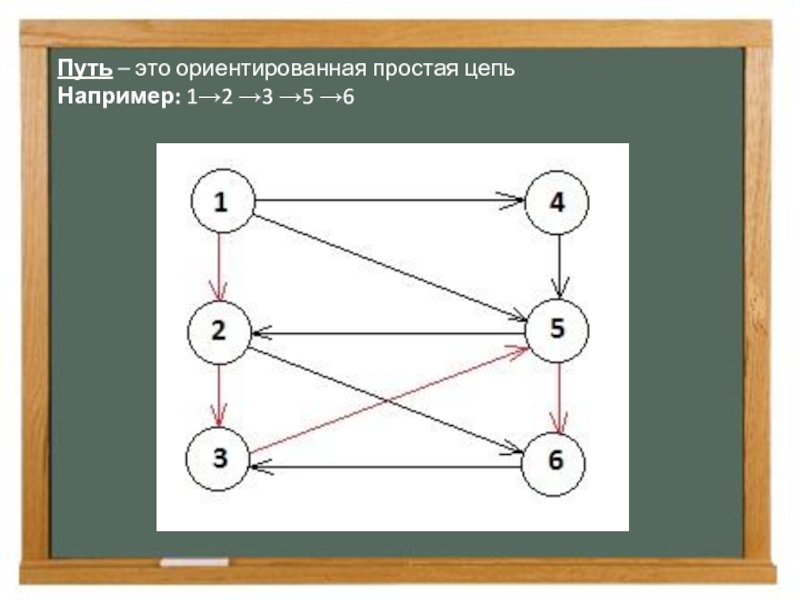
- 7. Путь – это ориентированная простая цепь Например: 1→2 →3 →5 →6
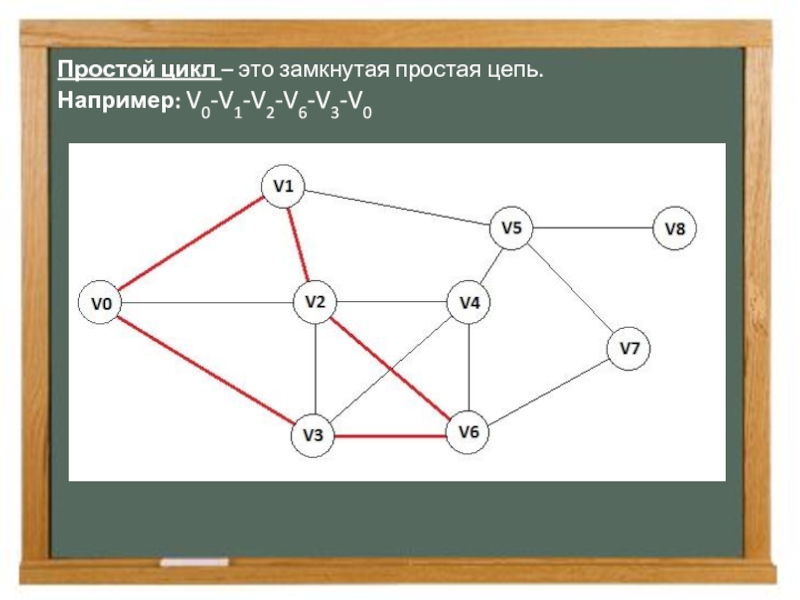
- 8. Простой цикл – это замкнутая простая цепь. Например: V0-V1-V2-V6-V3-V0
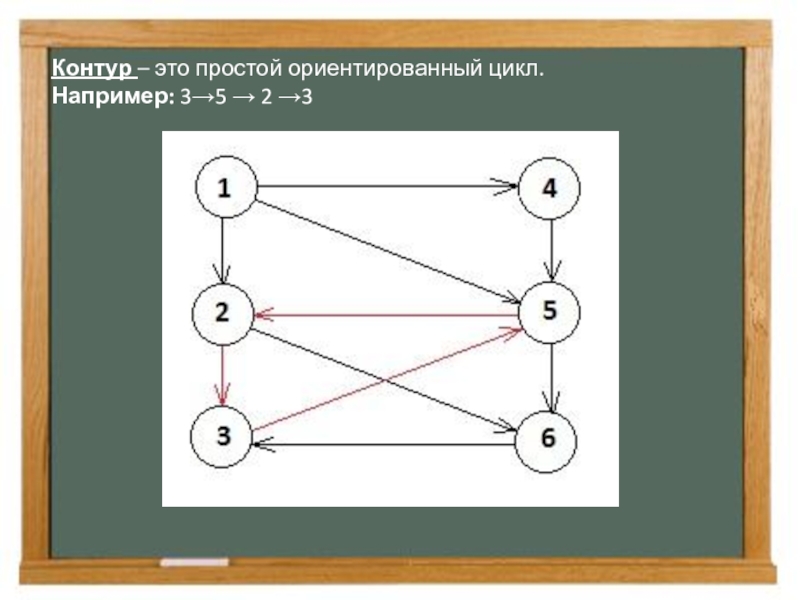
- 9. Контур – это простой ориентированный цикл. Например: 3→5 → 2 →3
- 10. Леонард Эйлер (1707 —1783) Эйлеров
- 11. Расстояние между вершинами, диаметр, мост
- 12. Расстояние между вершинами – это длина кратчайшей
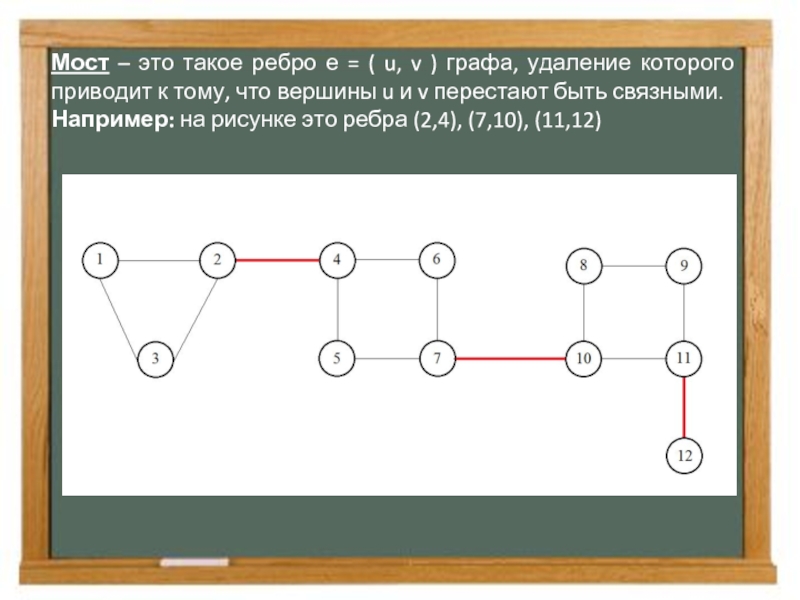
- 13. Мост – это такое ребро е =
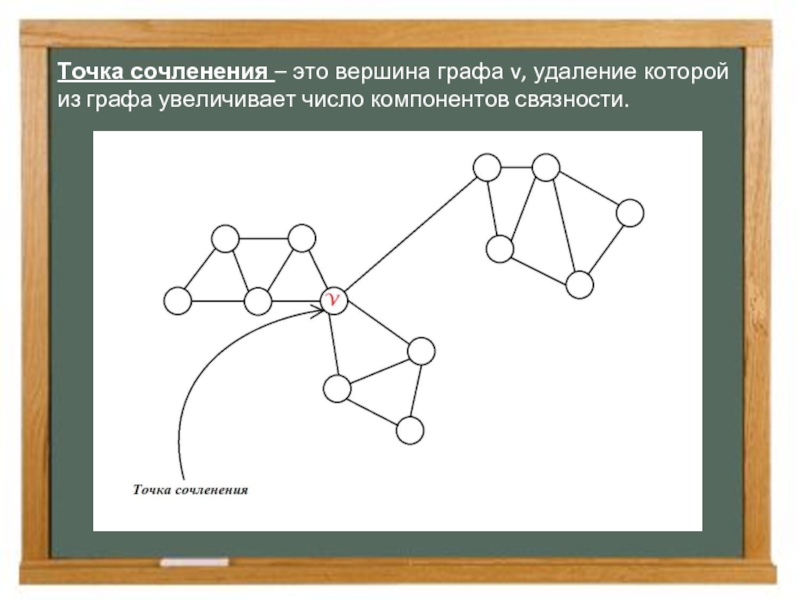
- 14. Точка сочленения, блок
- 15. Точка сочленения – это вершина графа v, удаление которой из графа увеличивает число компонентов связности.
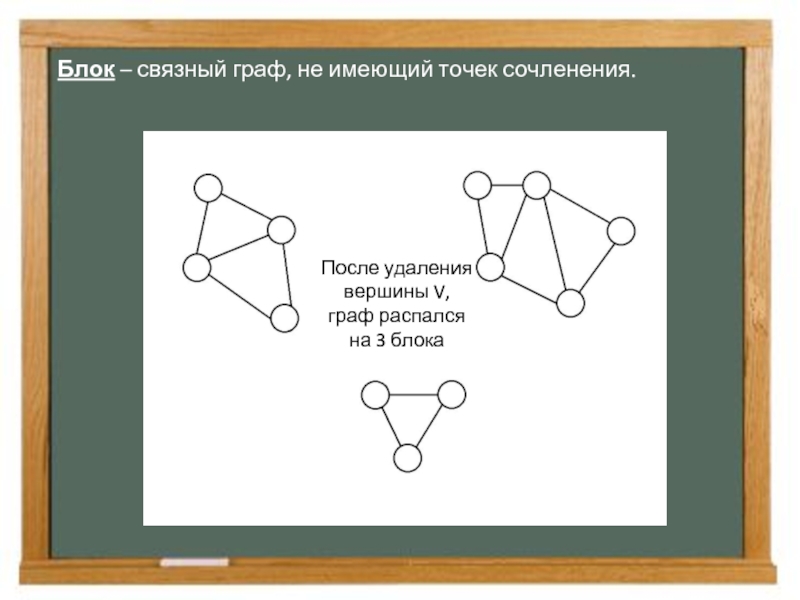
- 16. Блок – связный граф, не имеющий точек
- 17. Спасибо за внимание!
- 18. Выполнили: Студенты группы №953 Вдовин Роман Матвеева
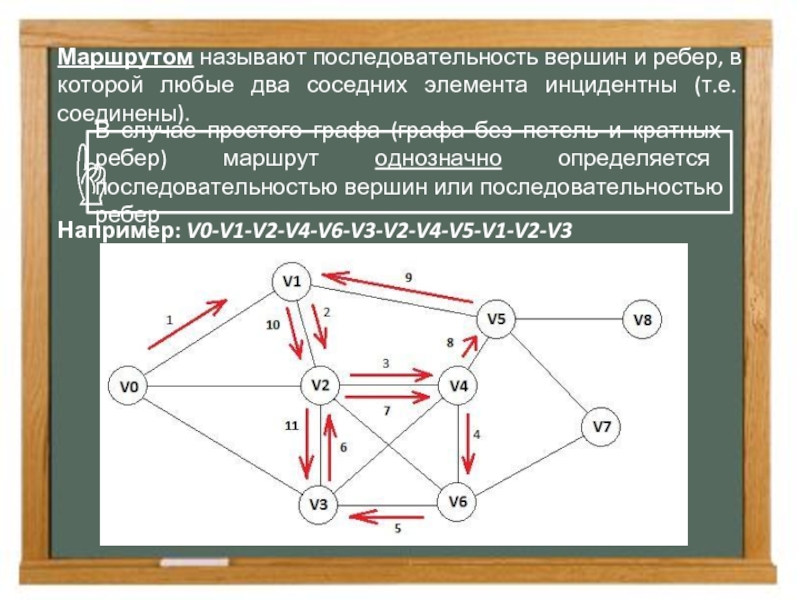
Слайд 3Маршрутом называют последовательность вершин и ребер, в которой любые два соседних
Например: V0-V1-V2-V4-V6-V3-V2-V4-V5-V1-V2-V3
В случае простого графа (графа без петель и кратных ребер) маршрут однозначно определяется последовательностью вершин или последовательностью ребер
☝
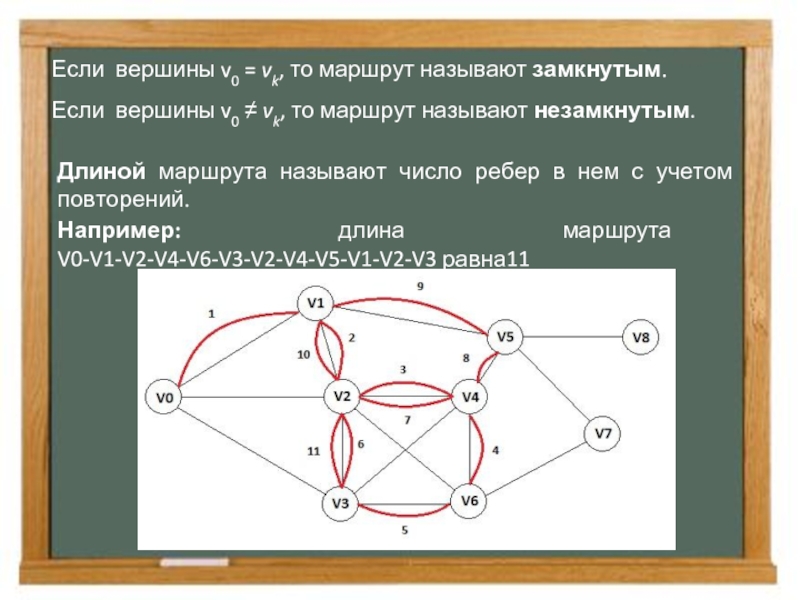
Слайд 4Если вершины v0 = vk, то маршрут называют замкнутым.
Если вершины v0
Длиной маршрута называют число ребер в нем с учетом повторений.
Например: длина маршрута V0-V1-V2-V4-V6-V3-V2-V4-V5-V1-V2-V3 равна11
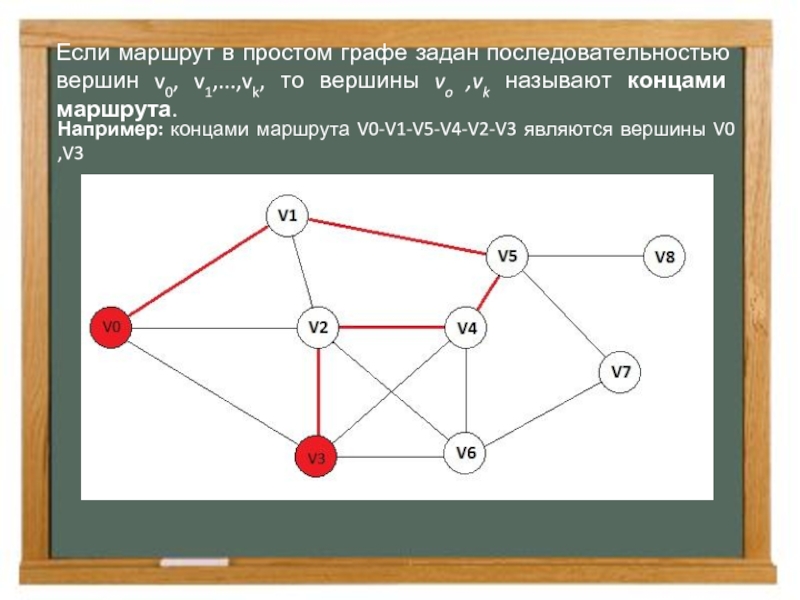
Слайд 5Если маршрут в простом графе задан последовательностью вершин v0, v1,...,vk, то
Например: концами маршрута V0-V1-V5-V4-V2-V3 являются вершины V0 ,V3
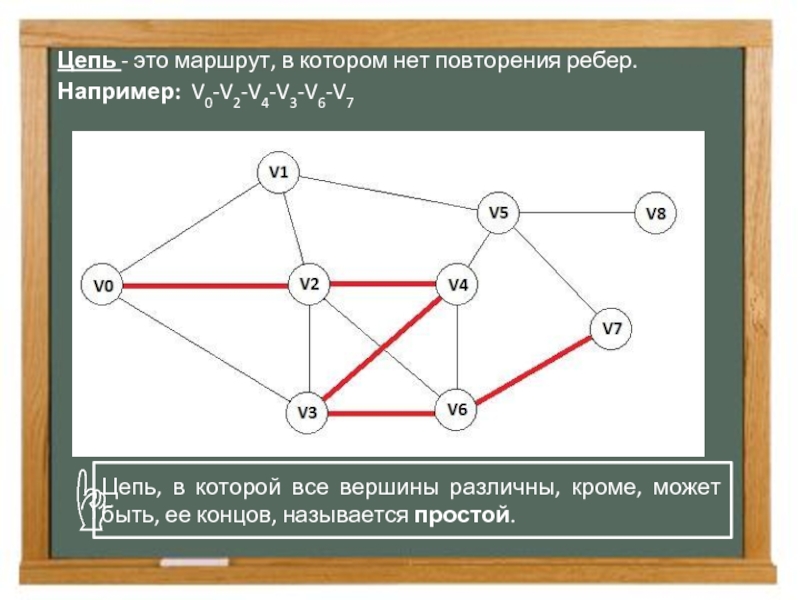
Слайд 6Цепь - это маршрут, в котором нет повторения ребер.
Например: V0-V2-V4-V3-V6-V7
Цепь,
☝
Слайд 10
Леонард Эйлер
(1707 —1783)
Эйлеров путь (эйлерова цепь) — это путь, проходящий по
Эйлеров цикл — это эйлеров путь, являющийся циклом.
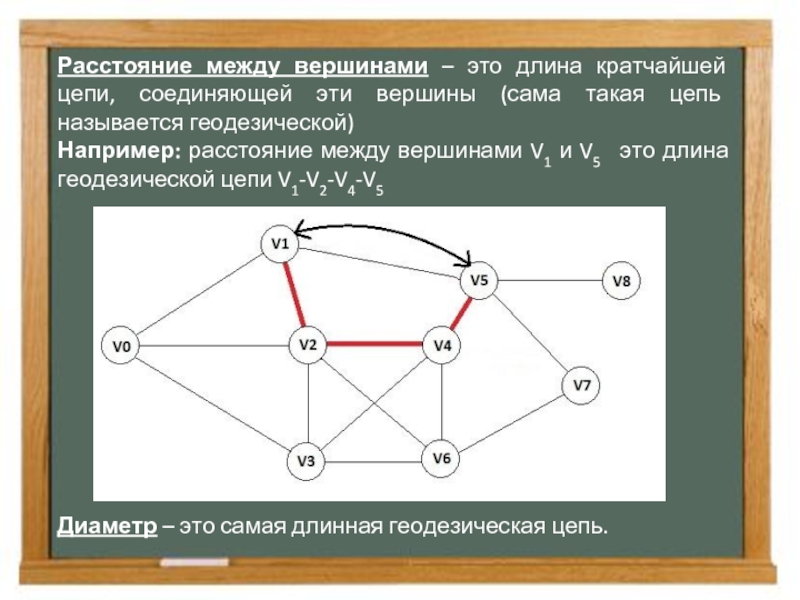
Слайд 12Расстояние между вершинами – это длина кратчайшей цепи, соединяющей эти вершины
Например: расстояние между вершинами V1 и V5 это длина геодезической цепи V1-V2-V4-V5
Диаметр – это самая длинная геодезическая цепь.
Слайд 13Мост – это такое ребро е = ( u, v )
Например: на рисунке это ребра (2,4), (7,10), (11,12)
Слайд 15Точка сочленения – это вершина графа v, удаление которой из графа
Слайд 16Блок – связный граф, не имеющий точек сочленения.
После удаления вершины V,
Слайд 18Выполнили:
Студенты группы №953
Вдовин Роман
Матвеева Ольга
Молодчикова Алена
Источники:
Учебник «Дискретная математика. Курс лекций» Палий
http://fc-iek.ucoz.ru
http:// irina-m.at.ua
Материал из Википедии: статья «Эйлеров цикл»