- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛУсДП презентация
Содержание
- 1. ЛУсДП
- 2. Что надо знать? Линейное уравнение с двумя
- 3. Что надо понимать? В первую очередь это
- 4. 2х+3у 12 Это равенство верно, если х=1,5
- 5. 2х+3у 12 Это равенство неверно, если х=3
- 6. 2х+3у 12 Это равенство неверно, если х=5
- 7. Что ещё надо знать? Те пары чисел,
- 8. Что ещё надо понимать? Во вторую очередь
- 9. Например, 2х+3у=12 Если я захочу вместо х
- 10. Что надо уметь? 1. Находить значение одной
- 11. Что надо уметь? 1. Находить значение одной
- 12. Что надо уметь? 1. Находить значение одной
- 13. Что ещё надо уметь? 2. Для заданного
- 14. Что ещё надо уметь? Для того,
- 15. Что ещё надо уметь? 2. Для заданного
- 16. 2. Для заданного уравнения строить его график
- 17. 2. Для заданного уравнения строить его график
- 18. Итак, Надо знать 2 факта: Какие формулы
Слайд 2Что надо знать?
Линейное уравнение с двумя переменными имеет вид ax+by=c или
ax+by+c=0
Например,
a, b, c – конкретные числа, у каждого уравнения свои
Здесь a=2, b=3, c=12
Например, х–3у+7=0
Здесь a=1, b=–3, c=7
Слайд 3Что надо понимать?
В первую очередь это уравнение.
То есть это равенство,
а иногда – нет.
Например, 2х+3у=12
Слайд 42х+3у
12
Это равенство верно, если х=1,5 и у=3
Действительно, если х=1,5 и у=3,
Слайд 52х+3у
12
Это равенство неверно, если х=3 и у=1
Действительно, если х=3 и у=1,
Слайд 62х+3у
12
Это равенство неверно, если х=5 и у=1
Действительно, если х=5 и у=1,
Слайд 7Что ещё надо знать?
Те пары чисел, которые дают верное равенство, называют
Например, 2х+3у=12
Пара чисел х=1,5 и у=3 является решением уравнения, так как 2∙1,5+3∙3=12
Пара чисел х=3 и у=1 не является решением уравнения, так как 2∙3+3∙1≠12
Пара чисел х=5 и у=1 не является решением уравнения, так как 2∙5+3∙1≠12
Слайд 8Что ещё надо понимать?
Во вторую очередь это уравнение с двумя переменными.
Это значит, что вместо х и у можно подставлять разные числа, но не как попало, а связанно друг с другом.
Например, 2х+3у=12
Если я захочу вместо х подставить число 0, то мне придётся подставить вместо у число 4, потому что 2∙0+3∙4=0+12=12
Слайд 9Например, 2х+3у=12
Если я захочу вместо х подставить число 15, то мне
2∙15+3∙(–6 )=30–18=12
Слайд 10Что надо уметь?
1. Находить значение одной переменной, если задано значение другой.
Например,
Если х=0, то, подставив, получим
2∙0+3∙у=12
Дальше нужно найти значение у, решая уравнение
0+3у=12
3у=12
у=12:3
у=4
Итак, если х=0, то у=4.
Слайд 11Что надо уметь?
1. Находить значение одной переменной, если задано значение другой.
Например,
Если х=5, то, подставив, получим
2∙5+3∙у=12
Дальше нужно найти значение у, решая уравнение
10+3у=12
3у=12–10
у=2
у=2:3
у=
Итак, если х=4, то у= .
Слайд 12Что надо уметь?
1. Находить значение одной переменной, если задано значение другой.
Например,
Если у=–4, то,
Итак, если у=–4, то х=12.
Иногда нужное значение можно вычислить «в уме», не решая уравнения.
Если у=–4, то, подставив, получим
2∙х+3∙(–4)=12
Дальше нужно найти значение у, решая уравнение
2х–12=12
2х=12+12
2х=24
х=24:2
х=12
Слайд 13Что ещё надо уметь?
2. Для заданного уравнения строить его график
Графиком любого
Для того, чтобы построить график, нужно выполнить следующую последовательность шагов (алгоритм):
Выбрать вместо переменной х какое-нибудь число. Вычислить у. Это будут координаты точки А.
Выбрать вместо х какое-нибудь другое число. Вычислить соответствующее ему у. Это будут координаты точки В.
Ввести систему координат хОу. Отметить точки А и В.
Провести через них прямую.
Слайд 14Что ещё надо уметь?
Для того, чтобы построить график, нужно выполнить следующую
Выбрать вместо переменной х какое-нибудь число. Вычислить у. Это будут координаты точки А.
Выбрать вместо х какое-нибудь другое число. Вычислить соответствующее ему у. Это будут координаты точки В.
Ввести систему координат хОу. Отметить точки А и В.
Провести через них прямую.
Замечание 1. Вместо х можно подобрать любое (в пределах разумного) число.
Замечание 2. Часто удобно использовать число 0.
Замечание 3. Часто для подбора второй точки удобно взять у=0 и вычислить соответствующее ему х.
Слайд 15Что ещё надо уметь?
2. Для заданного уравнения строить его график
Например, 2х+3у=12
Пусть
Как уже мы рассмотрели в предыдущих слайдах, в таком случае можно определить, что у=4. Первая точка А(0; 4).
Пусть теперь у=0, тогда 2∙х+3∙0=12.
В таком случае можно определить, что х=6. Вторая точка В(6; 0).
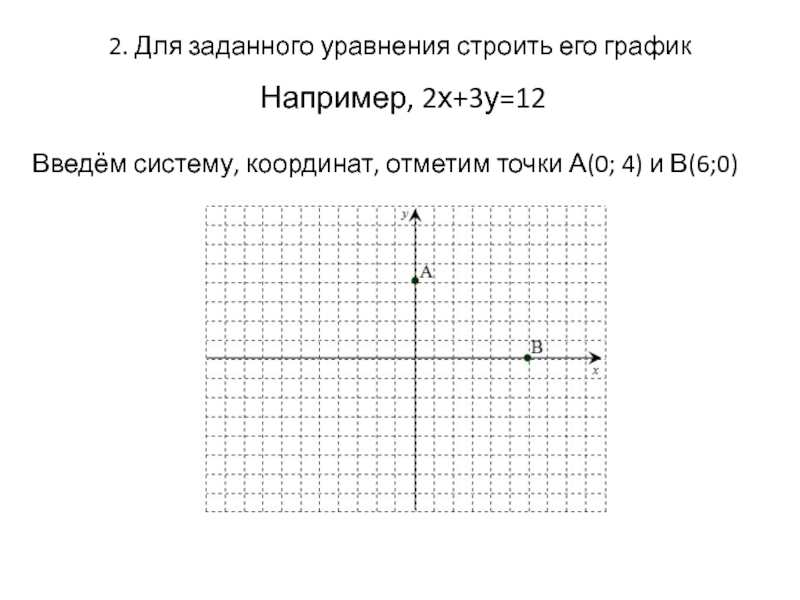
Слайд 162. Для заданного уравнения строить его график
Например, 2х+3у=12
Введём систему, координат, отметим
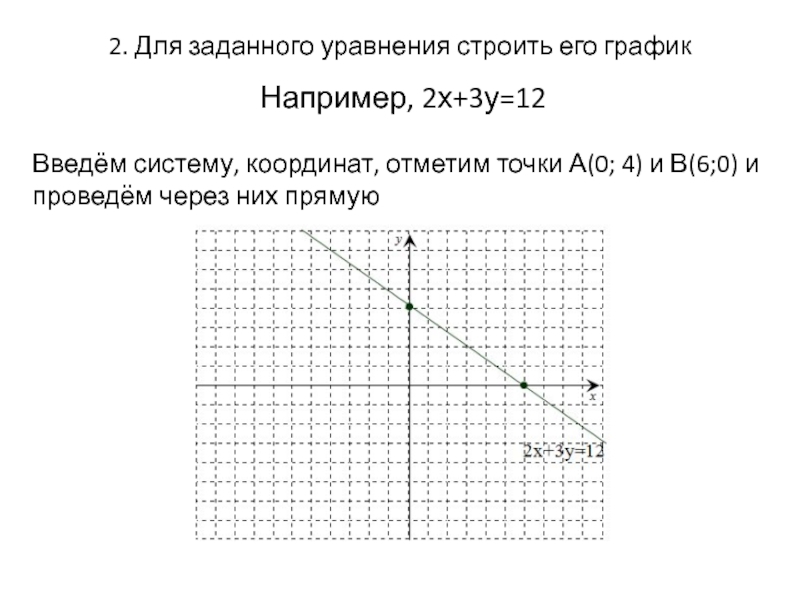
Слайд 172. Для заданного уравнения строить его график
Например, 2х+3у=12
Введём систему, координат, отметим
Слайд 18Итак,
Надо знать 2 факта:
Какие формулы относят к линейным уравнениям с двумя
Какие пары чисел считают решениями линейного уравнения с двумя переменными.
Надо понимать 2 обстоятельства:
Несмотря на то, что эта формула содержит две буквы (переменные), его смысл такой же как и у привычных с младших классов уравнений с одним неизвестным.
Две переменные в таком уравнении могут принимать разные значения (такие уравнения имеют бесконечно много решений), но значения обеих букв зависят друг от друга.
Надо уметь решать 2 задачи:
Нахождение значения одной переменной по заданному значению другой переменной.
Построение графика линейного уравнения с двумя переменными.